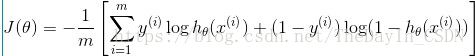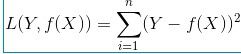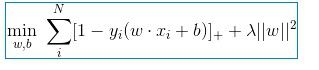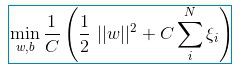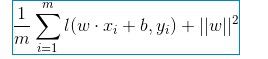深度学习自学（一）：Loss function 损失函数

                                 Loss function   2018.8.11    技术积淀篇

   面试经常被问到损失函数，想着有时间整理下，最常被问到的事在SVM和CNN中，一个是softmax，一个是hinge 函数，所以借鉴网上资料，自己也写上自己的见解，希望能给自己一个更深的理解，备注：学习无上限，学到的永远是自己的，请善待自己，珍惜时光。

一、损失函数简介

   损失函数（loss function）是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。CNN中主要是利用实际值与期望值做差，得出损失函数，并且反向传播。在SVM概念出现时，主要利用经验风险结构风险来引出，损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分，结构风险函数包括了经验风险项和正则项：                                                                                          

前面的均值函数表示的是经验风险函数，L代表的是损失函数，后面的是正则化项（regularizer）或者叫惩罚项（penalty term），它可以是L1，也可以是L2，或者其他的正则函数。这里主要是找出使目标函数最小时的值，这样模型的拟合效果更好，更接近数据的真实情况。

二、各类损失函数

1、log对数损失函数：逻辑回归

      平方损失函数可以通过线性回归在假设样本是高斯分布的条件下推导得到，而在逻辑回归的推导中，它假设样本服从伯努利分布（0-1分布），然后求得满足该分布的似然函数，接着取对数求极值，而逻辑回归并没有求似然函数的极值，而是把极大化当做是一种思想，进而推导出它的经验风险函数为最小化负的似然函数（即max F(y, f(x)) —-> min -F(y, f(x)))。从损失函数的视角来看，它就成了log损失函数。

       损失函数L(Y, P(Y|X))表达的是样本X在分类Y的情况下，使概率P(Y|X)达到最大值，利用已知的样本分布，找到最有可能（即最大概率）导致这种分布的参数值，因为log函数是单调递增的，所以logP(Y|X)也会达到最大值，因此在前面加上负号之后，最大化P(Y|X)就等价于最小化L了。

       逻辑回归最后得到的目标式：如果是二分类的话，则m值等于2，如果是多分类，m就是相应的类别总个数。

      

2、平方损失函数：最小二乘法 

     最小二乘法是线性回归的一种，OLS将问题转化成了一个凸优化问题，在线性回归中，它假设样本和噪声都服从高斯分布，最后通过极大似然估计（MLE）可以推导出最小二乘式子。最小二乘的基本原则是：最优拟合直线应该是使各点到回归直线的距离和最小的直线，即平方和最小。OLS是基于距离的，而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢（即Mean squared error， MSE），主要有以下几个原因：简单，计算方便；欧氏距离是一种很好的相似性度量标准；在不同的表示域变换后特征性质不变。

      

Y-f(X)表示的是残差，整个式子表示的是残差的平方和，而我们的目的就是最小化这个目标函数值（注：该式子未加入正则项），也就是最小化残差的平方和（residual sum of squares，RSS）

3、指数损失函数：Adaboost

Adaboost算法是前向分步加法算法，是一个加和模型，损失函数就是指数函数。在Adaboost中，经过m此迭代之后，可以得到

Adaboost每次迭代时的目的是为了找到最小化下列式子时的参数 和G

而指数损失函数(exp-loss）的标准形式如下：

可以看出，Adaboost的目标式子就是指数损失，在给定n个样本的情况下，Adaboost的损失函数为：

Adaboost算法常用于人脸检测，haar/LBP特征+Adaboost算法将多个弱分类器进行分类，cascade将多个弱分类器级联，进行人脸检测识别。

4、Hinge损失函数：支持向量机

SVM是做常见的分类器，因为他支持多维，小数据量，线性非线性分类，分类效果显著。hinge损失函数就是SVM常用的损失韩式，主要是能够满足SVM的第二个条件，支持向量点不在分类边界的范围内。

直接变换 

前半部分中的就是hinge损失函数，而后面相当于L2正则项。

SVM求取核函数有如下：0-线性核；1-多项式核；2-RBF核；3-sigmoid核。

总结：参数越多，模型越复杂，而越复杂的模型越容易过拟合。过拟合就是说模型在训练数据上的效果远远好于在测试集上的性能。此时可以考虑正则化，通过设置正则项前面的hyper parameter，来权衡损失函数和正则项，减小参数规模，达到模型简化的目的，从而使模型具有更好的泛化能力。