动态仙人掌 系列题解之一——3464: 动态仙人掌 I
（重发下我这篇原发于 2014-03-18 的网易博客，原博客被网易莫名禁掉了。。被迫手动搬家，忧伤）
现在好像各种题目出树已经出烦了，开始出仙人掌了。什么时候咱们不出动态树了，搞个Link-Cut Cactus！最近不是流行可持久化吗？什么时候来个可持久化
Link-Cut Cactus！
我们对于一个结点x，我们记录x->prevE和x->nextE表示结点x在它所属的链上的前一条边和后一条边。（x->prevE是较浅的那一条，x->nextE是深度较深的那一条）
此图中x4想谋权篡位，x2要被迫下台。
首先我们可以知道，一个环编号如果在链中出现，那么肯定是出现了连续的一段。
我们用不同的颜色表示不同的环编号。那么一条链上肯定有很多个颜色段。如果一个颜色段没有出现在开头和结尾就意味着它们是完整的，我们就可以将这一段用最短路等效。但是问题就是怎么知道最短路长度。我们现在假设我们已经得到了两条链的信息，都是经过了这样的“中间环化简”，那么一般情况下，就会剩下一头一尾两个颜色段。一般情况下，左边的结尾处颜色与右边的开头处颜色相同。（此处我们暂时忽略我们之前所说的“两条链连接起来时中间会缺一条边”）
——applepi
概述
首先我强调一下关于数据结构维护信息的手法……
信息有很多种，比如和、最小值、最大值、异或和等等。
我们想用数据结构维护信息，常用的方法就是合并两个已知的信息。也就是说，信息如果能够合并，那么就可以很爽地通过子结构的信息的合并来获得所需要的信息。比如sum、min、max、xor等等。
也就是说，假设有个结构A，有个结构B，我们想知道的信息用函数f表示，如果知道f(A)知道f(B)能求出f(A + B)，那么这个信息就是可合并的。
当然如果信息可减那就更好了。如果知道f(A)知道f(B)能求出f(A - B)，那么这个信息就是可减的。比如sum、xor就是这样的东西，而min、max不是。
其实这样讨论的时候我们忽略了一个东西：原子。一个结构并不总是由子结构组成，等到拆分到不能再拆分的时候，剩下的东西我们称之为原子。在某些情况下，维护原子信息其实比合并操作更加复杂。
还有个神奇的东西叫懒标记。比如结构A中的每个元素同时加上delta之类。而修改这东西本质上是个算子。那么如果想实现懒标记的话，就必须使得知道f(A)和修改算子m就能求出f(m A)。
……我写这题时由于一些细节问题无法解决，重写了若干次。
其实纠结来纠结去还是这几个倒霉：
1. 我维护什么信息？
2. 怎么合并？
3. 怎么维护原子信息？
4. 怎么实现修改算子？
忽视了其中任何一条，就得重写了。我不禁头涔涔而泪潸潸了……
在被虐了无数次之后，我得出的结论是……在设计数据结构的时候，如果不能保证：
除子结构和父结构外，一个结构维护的数据不会被其它结构维护。
恐怕就会面临重写了……
虽然一个结构里多记录点信息确实很诱人……但是我在这里说这些看起来像废话一样的东西希望不要再有人重蹈覆辙……
动态仙人掌 I
那么我们不闲扯了来说I吧！
能link、cut、查询最短路。
还有一个surprise的地方就是可能加边操作不合法……要自动无视。
我们先不管最短路的事，
从surprise开刀吧。
“每条边至多在一个简单环上”
ok!可做了吧！
做法就是，取仙人掌的一棵生成树进行维护，那么我们还剩下一坨非树边是游离态的。
一条非树边就对应着一个环。我们把环编号，并且我们把环上的所有边标上环的编号。我们称之为环编号。
那么我们想，如果有一条边处于两个环上，那么它就会领到两个环编号。
于是就显然了。link v u的时候，如果v、u不在一个仙人掌里，就直接接起来好了。如果在，那么说明要加一条非树边。我们检查所对应的路径上的所有边是不是均无环编号。如果有环编号直接输出failed，否则把这条路径上的所有边标上环编号。
当我们要cut v u的时候道理是一样的。如果这家伙是非树边，直接删掉把对应的路径上的边的环编号清空。否则是树边，讨论是否在环上。如果不在直接删掉，如果在，就清除对应环上所有边的环编号，删掉后把那个环对应的非树边的两端link起来。也就是说把非树边升级为树边。
于是只需要一棵link-cut tree就可以了！
为了说话方便，以下对于一个splay树中结点x：
x->fa表示x的父亲
x->lc表示x的右儿子。
x->rc表示x的右儿子。
x->msg表示维护的
splay中以x为根的子树的信息。也就是这个子树所代表的链信息。
wait！lct怎么维护边的信息啊！
在边上加个点：v ----- u ==========> v --- e --- u ？？？
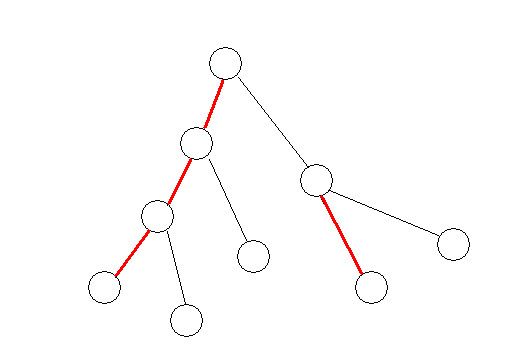
我有特别的维护边信息的技巧。首先我们要知道，lct是用splay维护了一个树的链剖分对吧。
就像这样：（红边表示实边）
特别地我们还要考虑边界情况。如果一个结点x不是preferred child，换句话说是这条链的顶端，那么x->prevE仍然是x到x的父亲的边，而如果没有preferred child，也就是说是链的底端，那么x->nextE为空。
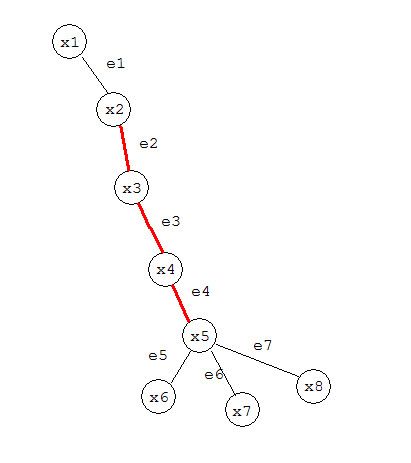
举个例子：
下图中
x2->prevE = e1, x2->nextE = e2。
x3->prevE = e2, x3->nextE = e3。
x5->prevE = e4, x5->nextE = NULL。
这样一来，splay树的一个子树所能感知到的世界就是这样的：
那么我们应该维护怎样的链信息？
我们应该明确一点，就是
链信息
中是不能包含有关
在
开头结尾裸露着的那两条边的信息的。因为这样就会导致有多个结构都在统计这条边。别人如果打了个标你就sb了。
也就是说我们的
链信息
一定只是关于那些结点和有头有尾的那些边的。
为了判断是不是仙人掌图，我们需要知道这一段链上有没有环编号。所以记录布尔变量x->msg->hasCir
每条边的环编号作为
原子信息。
合并的话直接x->msg->hasCir = x->lc->msg->hasCir || x->rc->msg->hasCir吗？
显然不是！
这样的话合并时两边会缺少两条中间进行衔接的边的信息。（x->prevE和x->nextE）
所以我们不得不记录一下这条链的开头和结尾裸露着的那两条边是什么。放在x->msg->firstE, x->msg->lastE中。
（不过如果不是信心满满……一定不要试图去查看x->msg->firstE和
x->msg->
lastE的原子信息。 = =）
合并的时候把这两条边考虑进去就大功告成了。
在access的时候，需要调整部分x的x->prevE和x->nextE。考察一次换边操作：
那么我们仔细想想，需要修改的其实只有x1->nextE而已，其它的维持不变。
也就是说x1->nextE = x4->prevE。
但是我们仔细想想access(x)的过程：
access(x)
{
for (p = x, q = NULL; p; q = p, p = p->fa)
{
splay(p);
p->rc = q;
p->update();
}
}
你会发现我们并不知道之前提到的“x4”在哪里。
而x4其实是这条链的顶端。如果我们想找到它，就得从q出发不断往左儿子走，这样就破坏了lct的均摊分析退化为O(log^2n)。
但是我们发现我们反正要找的东西是x4->prevE，而这就是q->msg->firstE，这样就解决了问题。
这样我们在access中途只要不断地x->nextE = q->msg->firstE即可了。
下面我们考虑各种各样的修改。目前有两种：一个是为了makeRoot(x)所需的链翻转标记，一个是为了维护环编号的区间覆盖标记。
我们要铭记我们的修改算子其实也不包括位于开头结尾裸露着的那两条边。所以下传与普通下传不同。
tag_down(x)
{
对x执行修改
if (x->lc)
{
对x->prevE执行修改
对x->lc打标
}
if (x->rc)
{
对x->nextE执行修改
对x->rc打标
}
}
链翻转标记很简单，直接把各种prevE、nextE、firstE、lastE之类的换一换就行了。
区间覆盖标记的话把x->msg->hasCir改一改就好了，下传时改一改x->prevE和x->nextE的环编号就好了。不过要注意的是叶子结点的情况……（调了N久……= =）
这样我们就解决了surprise。
我们考虑最短路。于是我们要维护更多的信息。
我们立刻意识到，考虑了环编号之后，splay树的一棵子树能感知到的世界更丰富了：
最理想的情况下是，这一段离那个完整的环只差一条非树边。如蓝环。
但是往往有坑爹情况：如
绿环，虽然形成了连续的一段，但不完整，有一些是裸露在外面的。
更坑爹的还有
红环。还有一部分不是处于跟自己一条链上的。这一部分是未知的世界。
我
们先着手处理绿环。那么我们可以得到一个直截了当的思路：
那么现在有两条链的信息要接起来，怎么办呢？我们要知道另一条路的长度。红环的困境就在于此。
这时我们发现其实这个很好办到，因为长度信息可减。我们可以记录下来每个环的长度。当我们想接起来的时候，拿：
总绿环长 - 已知绿色总长
就可以得到另一条路的长度。
所以只要拿：
min{
已知绿色总长,
总绿环长 - 已知绿色总长
}
就可以求得最短路长度。
所以我们需要记录：
x->msg->headLen, x->msg->midLen, x->msg->tailLen
为了顺利实现合并，需要通过一定的讨论解决：
没有开头颜色段
没有结尾颜色段
开头结尾是同一个颜色段
的情况。
对于两条链接起来中间会缺一条边的情况，随便搞搞就行了。这个不是大问题。
此处边的原子信息里就多了一个边权信息。
翻转和区间覆盖的时候也要相应的调整。
详细情况不再赘述……其它细节使劲乱搞讨论就行了。
这样我们就顺利解决了动态仙人掌 I。
在II中还要求回答最短路上边权的最小值，于是这个算法就行不通了，因为最小值不可减。
……其实这个算法在三道题中算比较好弄的？我是先YY出了II的解法，结果有天@hzhwcmhf过来把只回答最短路长度的这题给用这个算法秒了……于是我赶紧加了个回答最小值……而把只求最短路长度作为I给大家水水……
由于我比较懒……没有单独写I的标程，我直接把II的标程改了改。所以就没办法提供代码示例了 T_T……（不过反正大家都能用脚丫子把这题给A掉吧……无伤大雅）
（我是嘴巴选手我自豪，如果不好写不要找我麻烦）
update：我写了一份……现在放出来：
#include #include
#include #include
#include #include
#include #include
#include #include
#include
#include
using namespace std;
const int INF = INT_MAX;
const int MaxN = 100000;
inline int getint()
{
char c;
while (c = getchar(), '0' > c || c > '9');
int res = c - '0';
while (c = getchar(), '0' <= c && c <= '9')
res = res * 10 + c - '0';
return res;
}
template
class BlockAllocator
{
private:
static const int BlockL = 10000;
union TItem
{
char rt[sizeof(T)];
TItem *next;
};
TItem *pool, *tail;
TItem *unused;
public:
BlockAllocator()
{
pool = NULL;
unused = NULL;
}
T *allocate()
{
TItem *p;
if (unused)
{
p = unused;
unused = unused->next;
}
else
{
if (pool == NULL)
pool = new TItem[BlockL], tail = pool;
p = tail++;
if (tail == pool + BlockL)
pool = NULL;
}
return (T*)p;
}
void deallocate(T *pt)
{
TItem *p = (TItem*)pt;
p->next = unused, unused = p;
}
};
struct edge
{
int v, u, w;
int totL;
};
struct lct_edge
{
int w;
edge *cirE;
edge *getCirE()
{
return this ? this->cirE : NULL;
}
};
struct lct_message
{
int headL, midL, tailL;
lct_edge *firstE, *lastE;
bool hasCirE;
void rev()
{
swap(firstE, lastE);
swap(headL, tailL);
}
void coverCirE(edge *e, bool isSingle)
{
hasCirE = isSingle ? false : e != NULL;
}
friend inline lct_message operator+(const lct_message &lhs, const lct_message &rhs)
{
lct_message res;
res.firstE = lhs.firstE, res.lastE = rhs.lastE;
assert(lhs.lastE == rhs.firstE);
lct_edge *e = lhs.lastE;
res.hasCirE = lhs.hasCirE || e->cirE || rhs.hasCirE;
if (lhs.tailL != -1 && rhs.headL != -1)
{
res.headL = lhs.headL;
res.tailL = rhs.tailL;
int trL = lhs.tailL + e->w + rhs.headL;
res.midL = lhs.midL + min(trL, e->cirE->totL - trL) + rhs.midL;
}
else if (lhs.tailL != -1)
{
res.headL = lhs.headL;
res.tailL = lhs.tailL + e->w + rhs.midL;
res.midL = lhs.midL;
}
else if (rhs.headL != -1)
{
res.headL = lhs.midL + e->w + rhs.headL;
res.tailL = rhs.tailL;
res.midL = rhs.midL;
}
else
{
res.headL = lhs.headL;
res.tailL = rhs.tailL;
res.midL = lhs.midL + e->w + rhs.midL;
}
return res;
}
};
struct lct_node
{
lct_node *fa, *lc, *rc;
lct_edge *prevE, *nextE;
lct_message msg;
bool hasRev;
bool hasCoveredCirE;
edge *coveredCirE;
bool isRoot()
{
return !fa || (fa->lc != this && fa->rc != this);
}
void rotate()
{
lct_node *x = this, *y = x->fa, *z = y->fa;
lct_node *b = x == y->lc ? x->rc : x->lc;
x->fa = z, y->fa = x;
if (b)
b->fa = y;
if (z)
{
if (y == z->lc)
z->lc = x;
else if (y == z->rc)
z->rc = x;
}
if (x == y->lc)
x->rc = y, y->lc = b;
else
x->lc = y, y->rc = b;
y->update();
}
void allFaTagDown()
{
int anc_n = 0;
static lct_node *anc[MaxN];
anc[anc_n++] = this;
for (int i = 0; !anc[i]->isRoot(); i++)
anc[anc_n++] = anc[i]->fa;
for (int i = anc_n - 1; i >= 0; i--)
anc[i]->tag_down();
}
void splay()
{
allFaTagDown();
while (!this->isRoot())
{
if (!fa->isRoot())
{
if ((fa->fa->lc == fa) == (fa->lc == this))
fa->rotate();
else
this->rotate();
}
this->rotate();
}
this->update();
}
void splay_until(lct_node *target)
{
allFaTagDown();
while (this->fa != target)
{
if (fa->fa != target)
{
if ((fa->fa->lc == fa) == (fa->lc == this))
fa->rotate();
else
this->rotate();
}
this->rotate();
}
lct_node *x = this;
while (!x->isRoot())
x->update(), x = x->fa;
x->update();
}
lct_node *lmost()
{
lct_node *x = this;
while (x->tag_down(), x->lc)
x = x->lc;
return x;
}
void access()
{
for (lct_node *p = this, *q = NULL; p; q = p, p = p->fa)
{
p->splay();
p->nextE = q ? q->msg.firstE : NULL;
p->rc = q;
}
this->splay();
}
void makeRoot()
{
this->access();
this->tag_rev();
this->tag_down();
}
lct_node *findRoot()
{
this->access();
lct_node *root = this->lmost();
root->splay();
return root;
}
void tag_rev()
{
hasRev = !hasRev;
msg.rev();
}
void tag_coverCirE(edge *e)
{
hasCoveredCirE = true, coveredCirE = e;
msg.coverCirE(e, !lc && !rc);
}
void tag_down()
{
if (hasRev)
{
swap(lc, rc);
swap(prevE, nextE);
if (lc)
lc->tag_rev();
if (rc)
rc->tag_rev();
hasRev = false;
}
if (hasCoveredCirE)
{
if (lc)
{
prevE->cirE = coveredCirE;
lc->tag_coverCirE(coveredCirE);
}
if (rc)
{
nextE->cirE = coveredCirE;
rc->tag_coverCirE(coveredCirE);
}
hasCoveredCirE = false;
}
}
void update()
{
if (prevE->getCirE() == nextE->getCirE())
msg.headL = msg.tailL = -1;
else
{
msg.headL = prevE->getCirE() ? 0 : -1;
msg.tailL = nextE->getCirE() ? 0 : -1;
}
msg.midL = 0;
msg.hasCirE = false;
msg.firstE = prevE, msg.lastE = nextE;
if (lc)
this->msg = lc->msg + this->msg;
if (rc)
this->msg = this->msg + rc->msg;
}
};
lct_node lctVer[MaxN + 1];
BlockAllocator lctCirEAllocator;
BlockAllocator lctEAllocator;
int n;
void cactus_init()
{
for (int v = 1; v <= n; v++)
{
lct_node *p = lctVer + v;
p->fa = p->lc = p->rc = NULL;
p->prevE = p->nextE = NULL;
p->hasRev = false;
p->hasCoveredCirE = false;
p->update();
}
}
bool cactus_link(int v, int u, int w)
{
if (v == u)
return false;
if (v > u)
swap(v, u);
lct_node *x = lctVer + v, *y = lctVer + u;
x->makeRoot();
y->makeRoot();
if (x->fa)
{
x->access();
y->splay_until(x);
if (x->msg.hasCirE)
return false;
edge *cirE = lctCirEAllocator.allocate();
cirE->v = v, cirE->u = u, cirE->w = w;
cirE->totL = x->msg.midL + w;
y->nextE->cirE = cirE;
x->prevE->cirE = cirE;
if (y->rc)
y->rc->tag_coverCirE(cirE);
y->update(), x->update();
}
else
{
x->fa = y;
lct_edge *e = lctEAllocator.allocate();
e->w = w, e->cirE = NULL;
x->prevE = e;
x->update();
}
return true;
}
bool cactus_cut(int v, int u, int w)
{
if (v == u)
return false;
if (v > u)
swap(v, u);
lct_node *x = lctVer + v, *y = lctVer + u;
if (x->findRoot() != y->findRoot())
return false;
y->makeRoot();
x->access();
y->splay_until(x);
lct_edge *e = y->nextE;
edge *cirE = e->cirE;
if (cirE && cirE->v == v && cirE->u == u && cirE->w == w)
{
y->nextE->cirE = NULL;
x->prevE->cirE = NULL;
if (y->rc)
y->rc->tag_coverCirE(NULL);
y->update(), x->update();
lctCirEAllocator.deallocate(cirE);
return true;
}
if (!y->rc && e->w == w)
{
if (cirE)
{
y->nextE->cirE = NULL;
x->prevE->cirE = NULL;
}
y->nextE = NULL, x->prevE = NULL;
lctEAllocator.deallocate(e);
x->lc = NULL, y->fa = NULL;
x->update(), y->update();
if (cirE)
{
lct_node *ex = lctVer + cirE->v;
lct_node *ey = lctVer + cirE->u;
lct_node *rx = ex->findRoot();
lct_node *ry = ey->findRoot();
if (rx != ex)
{
ex->access();
rx->splay_until(ex);
ex->prevE->cirE = NULL;
rx->nextE->cirE = NULL;
if (rx->rc)
rx->rc->tag_coverCirE(NULL);
rx->update(), ex->update();
}
if (ry != ey)
{
ey->access();
ry->splay_until(ey);
ey->prevE->cirE = NULL;
ry->nextE->cirE = NULL;
if (ry->rc)
ry->rc->tag_coverCirE(NULL);
ry->update(), ey->update();
}
ex->makeRoot(), ey->makeRoot();
ex->fa = ey;
e = lctEAllocator.allocate();
e->w = cirE->w, e->cirE = NULL;
ex->prevE = e, ex->update();
lctCirEAllocator.deallocate(cirE);
}
return true;
}
return false;
}
int cactus_query(int qv, int qu)
{
lct_node *x = lctVer + qv, *y = lctVer + qu;
if (x->findRoot() != y->findRoot())
return -1;
x->makeRoot();
y->access();
return y->msg.midL;
}
int main()
{
int nQ;
cin >> n >> nQ;
cactus_init();
while (nQ--)
{
char type;
while (type = getchar(), type != 'l' && type != 'c' && type != 'd');
if (type == 'l')
{
int v = getint(), u = getint(), w = getint();
if (cactus_link(v, u, w))
printf("ok\n");
else
printf("failed\n");
}
else if (type == 'c')
{
int v = getint(), u = getint(), w = getint();
if (cactus_cut(v, u, w))
printf("ok\n");
else
printf("failed\n");
}
else if (type == 'd')
{
int v = getint(), u = getint();
printf("%d\n", cactus_query(v, u));
}
else
{
puts("error!");
}
}
return 0;
}