模型评估及评估指标
1 模型评估
模型评估是对训练好的模型性能进行评估,机器学习的任务有回归,分类和聚类,(见博客:机器学习基础概念),针对不同的任务有不同的评价指标,下文详解.
2 分类模型评价指标
2.1 一级指标
| 序号 | 一级指标 | 真实值 | 模型预测值 | 说明 |
|---|---|---|---|---|
| 1 | TP | True | Positive | 真正,即真实值和预测值均是正样本,表示预测正确 |
| 2 | TN | True | Negative | 真负,即真实值和预测值均为负样本,表示预测正确 |
| 3 | FN | False | Negative | 假负,即真实值为正,预测值为负,表示预测错误,若正表示通过,该参数可表示误拒率 |
| 4 | FP | False | Positive | 假正,即真实值为负,预测值为正,表示预测错误,若正表示通过,该参数可表示误入率 |
2.2 二级指标
| 序号 | 二级指标 | 计算 | 说明 |
|---|---|---|---|
| 1 | 准确率(ACC) | Accuracy= T P + T N T P + T N + F P + F N \frac{TP+TN}{TP+TN+FP+FN} TP+TN+FP+FNTP+TN | 分类模型预测正确的结果占总观测样本的比例,即所有预测结果中,预测正确的比例 |
| 2 | 精确率(PPV) | Precision= T P T P + F P \frac{TP}{TP+FP} TP+FPTP | 模型预测为Positive所有结果中,模型预测正确的比例,从预测角度出发,取出一类预测结果,评估预测准确率 |
| 3 | 灵敏度(TPR) | Sensitivity=Recall= T P T P + F N \frac{TP}{TP+FN} TP+FNTP | 真实值是Positive所有结果中,模型预测正确的比例,从真实值角度出发,取出一类结果,评估预测准确率,查全率 |
| 4 | 特异度(TNR) | Specificity= T N T N + F P \frac{TN}{TN+FP} TN+FPTN | 真实值是Negative所有结果中,模型预测正确的比例 |
2.3 三级指标
F 1 S c o r e F_1 Score F1Score是精度和召回率的调和平均数,通过该方法,取值较小会分配更高的权重,因此,只有当召回率和精度都很高时,分类器才会获得较高的 F 1 F_1 F1分数.
【F1 Score】
计算:
F 1 S c o r e = 2 1 P + 1 R = 2 P R P + R F_{1}Score=\frac{2}{\frac{1}{P}+\frac{1}{R}}=\frac{2PR}{P+R} F1Score=P1+R12=P+R2PR
其中,P为Precision,R为Recall,该参数综合了Precision和Recall的结果,取值范围[0, 1],0表示模型预测效果最差,1表示模型预测效果最好.
2.4 混淆矩阵
混淆矩阵是监督学习中的可视化工具,用于比较分类结果即预测结果和实际数据的匹配度,行表示预测类别,列表示实际类别.
2.4.1 矩阵
| 混淆矩阵 | 真实值 | ||
| Positive | Negative | ||
| 预测值 | Positive | TP | FP |
| Negative | FN | TN | |
2.4.2 例证
以人脸识别为例,人脸识别图片中的人脸是否在人脸库中,约定如下:若在则记为合法,不在则记为非法,人脸库共有250张人脸.
【(1) 混淆矩阵】
| 混淆矩阵 | 真实值 | ||
| 合法 | 非法 | ||
| 预测值 | 合法 | 100 | 40 |
| 非法 | 60 | 50 | |
【(2) 二级指标】
| 序号 | 二级指标 | 计算 | 说明 |
|---|---|---|---|
| 1 | 准确率(ACC) | Accuracy= T P + T N T P + T N + F P + F N = 150 250 \frac{TP+TN}{TP+TN+FP+FN}=\frac{150}{250} TP+TN+FP+FNTP+TN=250150=60% | 分类模型预测正确的结果占总观测样本的比例,即所有预测结果中,预测正确的比例 |
| 2 | 精确率(PPV) | Precision= T P T P + F P = 100 100 + 40 \frac{TP}{TP+FP}=\frac{100}{100+40} TP+FPTP=100+40100=71.4% | 模型预测为Positive所有结果中,模型预测正确的比例,从预测角度出发,取出一类预测结果,评估预测准确率 |
| 3 | 灵敏度(TPR) | Sensitivity=Recall= T P T P + F N = 100 100 + 60 \frac{TP}{TP+FN}=\frac{100}{100+60} TP+FNTP=100+60100=62.5% | 真实值是Positive所有结果中,模型预测正确的比例,从真实值角度出发,取出一类结果,评估预测准确率 |
| 4 | 特异度(TNR) | Specificity= T N T N + F P = 50 40 + 50 \frac{TN}{TN+FP}=\frac{50}{40+50} TN+FPTN=40+5050=55.5% | 真实值是Negative所有结果中,模型预测正确的比例 |
2.5 ROC和AUC
2.5.1 ROC
接受者操作特征曲线(Reciver Operating Characteristic Curve,ROC)曲线用于描述二分类系统性能(分类器阈值是变化的),反应敏感性和特异性连续变化的综合指标,ROC曲线上的点反应对同一信号刺激的感受性.ROC三种形式:
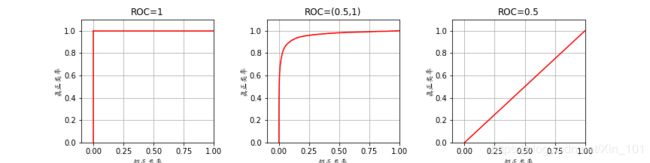
2.5.2 AUC
曲线面积(Area Under Curve,AUC)模型评价中定义为ROC曲线下的面积,取值[0, 1],由于ROC曲线一般在 y = x y=x y=x上方,因此AUC取值[0.5, 1],值越大,表明分类器效果越好.AUC三种取值:
| 序号 | AUC取值 | 描述 |
|---|---|---|
| 1 | 1 | 100%准确预测分类器,存在至少一个阈值可实现100%预测,实际不存在 |
| 2 | (0.5, 1) | 该情况优于随机猜测,设定合适的阈值,预测准确度高达90% |
| 3 | 0.5 | 该情况和正常的猜硬币一样,没有预测价值 |
| 4 | (0, 0.5) | 比随机猜测效果还差,若反预测,则预测效果优于随机猜测 |
2.6 AP与mAP
2.6.1 AP
精度平均值(Average Precision, AP)表征模型对某一类别物品评估的平均精度,即2.2节中二级指标:精度的平均值.
A P = ∑ P r e c i s i o n c N u m b e r c AP = \frac{\sum Precision_{c}}{Number_{c}} AP=Numberc∑Precisionc
其中,Precision为模型精度,见2.2节,c为某一物品类别,Number为某类物品验证集数量.
如有验证集自行车有200张图片,计算每张图片的精度,然后求200张图片精度的平均值,即为精度平均值.
A P = ∑ P r e c i s i o n b i k e 20 0 b i k e AP = \frac{\sum Precision_{bike}}{200_{bike}} AP=200bike∑Precisionbike
2.6.2 mAP
平均精度的均值(Mean Average Precision, mAP)即所有类别的平均精度.如10个类别,计算10个类别的平均精度的平均值.
m A P = ∑ i n A P i n mAP=\frac{\sum_i^n AP_{i}}{n} mAP=n∑inAPi
其中,AP为某一类别物品的平均识别精度,i为某一物品,n为物品种类数量.
如10个类别,计算10个类别的平均精度的平均值.
m A P = ∑ i 10 A P i 10 mAP=\frac{\sum_i^{10} AP_{i}}{10} mAP=10∑i10APi
3 回归模型评价指标
3.1 方差
方差(Variance, Var),反映数据集中数据离散程度。
V a r = 1 n ∑ i = 1 n ( y r e a l − μ ) 2 Var ={\frac{1}{n}\sum_{i=1}^{n}(y_{real}-\mu)^2} Var=n1i=1∑n(yreal−μ)2
其中, n n n为数据集数据数量, y r e a l y_{real} yreal训练数据集即真实的数据集, μ = 1 n ∑ i = 1 n y i \mu=\frac{1}{n}\sum_{i=1}^{n}y_i μ=n1∑i=1nyi为数据集均值.
3.2 标准差
标准差(Standard Deviation, SD)方差的平方根,反映数据集中数据离散程度.
S D = 1 n ∑ i = 1 n ( y r e a l − μ ) 2 SD=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_{real}-\mu)^2} SD=n1i=1∑n(yreal−μ)2
其中, n n n为数据集数据数量, y r e a l y_{real} yreal训练数据集即真实的数据集, μ = 1 n ∑ i = 1 n y i \mu=\frac{1}{n}\sum_{i=1}^{n}y_i μ=n1∑i=1nyi为数据集均值.
3.3 平均绝对误差
平均绝对误差(Mean Absolute Error, MAE),反映预测值和真实值的误差,更接近于实际情况.
M A E = 1 n ∑ i = 1 n ∣ ( y r e a l − y p r e d i c t ) ∣ MAE=\frac{1}{n}\sum_{i=1}^{n}|(y_{real}-y_{predict})| MAE=n1i=1∑n∣(yreal−ypredict)∣
其中, n n n为数据集数据数量, y r e a l y_{real} yreal训练数据集即真实的数据集, y p r e d i c t y_{predict} ypredict模型预测数据集.
3.4 平均平方误差
平均平方误差(Mean Squared Error, MSE)即均方误差,评价数据的变化程度,MSE越小,说明预测模型描述实验数据的准确率越高, 表示:
M S E = 1 n ∑ i = 1 n ( y r e a l − y p r e d i c t ) 2 MSE=\frac{1}{n}\sum_{i=1}^{n}(y_{real}-y_{predict})^2 MSE=n1i=1∑n(yreal−ypredict)2
其中, n n n为数据集数据数量, y r e a l y_{real} yreal训练数据集即真实的数据集, y p r e d i c t y_{predict} ypredict模型预测数据集,神经网络中的梯度下降方法中优化的数据就是均方误差.
3.5 均方根误差
均方根误差(Root Mean Squared Error)是均方根误差的算数平方根, 应用广泛,但是,它使用平均误差,对异常点(outliers)较敏感,如果回归器对某个点的回归值不理性,误差就会很大,从而对RMSE的值影响较大,平均值是非鲁棒性的,在训练神经网络模型时,为提高神经网络的鲁棒性(Robust),引入滑动平均模型,控制模型跟新速度,提高模型健壮性.
R M S E = 1 n ∑ i = 1 n ( y r e a l − y p r e d i c t ) 2 RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_{real}-y_{predict})^2} RMSE=n1i=1∑n(yreal−ypredict)2
其中, n n n为数据集数据数量, y r e a l y_{real} yreal训练数据集即真实的数据集, y p r e d i c t y_{predict} ypredict模型预测数据集.
4 总结
(1) 模型评估分为分类模型和回归模型评估,评估指标分别针对模型训练结束和训练过程中;
(2) 分类模型评估是模型训练结束后的评估,主要指标是 F 1 F_1 F1分数和ROC曲线和AUC曲线;
(3) 回归模型评估是模型训练过程的评估,这个评估是在训练时使用的手段,如训练神经网络过程中,梯度下降使用的均方误差进行优化,使用滑动平均模型提高模型鲁棒性;
(4) 机器学习训练分类模型的过程是先回归,回归评估(优化),在分类,分类优化,最后评估分类模型;
[参考文献]
[1]https://blog.csdn.net/Orange_Spotty_Cat/article/details/80520839
[2]http://www.cnblogs.com/guoyunzhe/p/6063495.html
[3]https://blog.csdn.net/tanzuozhev/article/details/79109311
[4]http://m.elecfans.com/article/712572.html
[5]https://www.cnblogs.com/zongfa/p/9431807.html
[6]https://blog.csdn.net/qq_31821675/article/details/82025527
[7]https://www.cnblogs.com/zongfa/p/9783972.html
