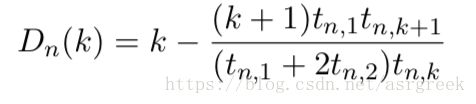图解N-gram语言模型的原理--以kenlm为例

常用的N-gram训练工具有SRILM、IRSTLM、BerkeleyLM和KenLM等。这几种工具所 用的算法思想基本一致，只是在实现细节上有所不同，所以我们只需理解其中一个训 练工具即可。本文以KenLM(号称速度最快，占用内存最少)作为训练工具，对基于N-gram的过程进行详细介绍，所用的平滑技术是Modified Kneser-ney smoothing，因为它是当 前一个标准的、广泛采用的、效果最好的平滑算法。

为了方便说明训练过程，我们以下列简单文本为例进行bigram操作:

我
你 我
他
我
你

对于KenLM工具，需要执行如下命令:lmplz -o 2 --text [inputfile] --arpa [outputfile]; 然后我们就可以得到如图1所示的bigram结果:

图1 bigram语言模型

---

接下来我们一步步剖析，看该结果是怎么生成的。

一、增加和标记符，表示句子的开头和结尾。

我
你 我
他
我
你 <

二、把每个词映射到唯一的数字id，为了更直观地描述下面的关键步骤，我们这里就不把单词映射为数字id。

三、Counting（原始计数）。也就是把相同的字合并，然后排序(假设编码顺序为、我、你、他、<\s>) 。根据步骤一的文本，我们可以得到1-gram和2-gram的原始计数:

表1 1-gram counting

1-gram	原始计数
	5
我	3
你	2
他	1
	5

表2 2-gram counting

2-gram	原始计数
我	2
你	2
他	1
我	3
你 我	1
你	1
他	1

四、Adjusting（调整计数）。其基本思想是对于那些lower-gram，我们不care其出现的次数，而是关心其作为novel continuation的可能性。比如“York”，其在语料中出现的次数一般会比较多，因为“New York”是很高频的词。但“York”作为continuation(中文意思:别的词把“york”作为接续词)的可能性就较低，也就是说它前面的词只有“new”等少数几类词，所以应该给它较低的计数。其公式如下:

(1)
式中：

• $w_1^n$表示某个n-gram，比如n=2时，那么$w_1^2$就表示表2中第一列的某个2-gram。
• $c(w_1^n)$表示$w_1^n$的原始计数;1-gram的原始计数见表1，2-gram的原始计数见表2;
• $a(w_1^n)$表示由原始计数调整后的计数;2-gram的调整后计数不变(根据式子(1)中的第一行)，还是如表2所示;1-gram的调整后计数见表3(根据式子(1)中的第二行得到的)。

下面详细介绍1-gram的调整计数的计算过程。特别需要说明的是公式(1)中的$\left|\upsilon :c\left(\upsilon w_1^n\right)\right|$表示$w_1^n$前面出现的词的种类，比如=“我”，词库中“我”出现2次，“你我”出现1次，那么“我”的前面出现的词的种类就为2，a(我)=2，而不是3，因为我们care的不是出现次数。根据这一原则，我们可以得到1-gram的调整计数，如下表所示：

而对于2-gram的adjusting count，根据式1的条件表达式(n=N)得,2-gram的adjusting count与表2相同。

五、Discounting。其基本思想是把经常出现的一些N-Gram的概率分一些出来给没有出 现的N-gram，也就等同于将经常出现的N-Gram次数减去(discount)一部分，这样做的道理就在于，对于出现次数比较多的计数我们其实已经得到了一个相对比较好的估计，那么当我们从这个计数值中减去一个较小的数值d后应该影响不大。那 到底该discount取多少呢?其中比较有代表性的有Church & Gale于1991年通过留存 法实验从而得到的Absolute Discounting;另一个是Chen and Goodman于1998年提出 的方法，其公式如下:

（2）
式中：

• k ε [1,3]；对于k为0的情况，$D_n\left(0\right)$=0；对于k大于3的情况，$D_n\left(k\right)$=$D_n\left(3\right)$；
• n ε [1,N]；比如在本例中我们采用2-gram，那么N=2，n=[1,2]；

在计算$D_n\left(k\right)$之前，我们需要先计算$t_{n,k}$。$t_{n,k}$表示出现了k次的n-gram的个数(比如根据表3，出现1次的1-gram的次数为2，分别为“你”、“他”)。其数学表达式如下：
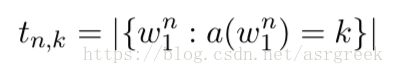（3）
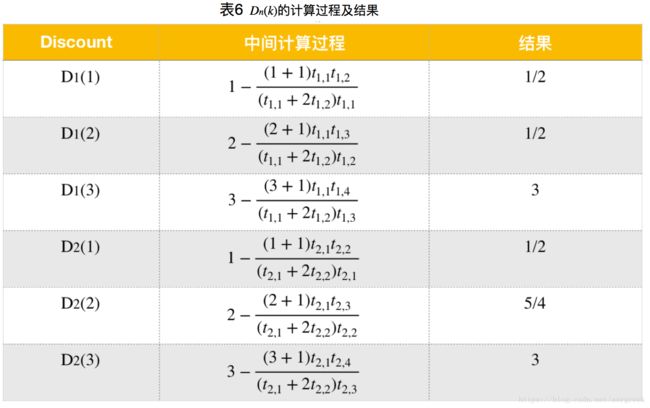
根据公式(3)、表3和表4，我们可以得到$t_{n,k}$的取值($t_{1,1}$至$t_{1,4}$的计算参考表3，$t_{2,1}$至$t_{2,4}$的计算参考表4)

根据公式(2)和表5，我们可以得到$D_n\left(k\right)$的取值：

六、Normalization。该步骤其实分为两小步:

① 计算n-gram的概率，该概率称之为pseudo probability，也就是说它不是最终的概率，但对于计算最终概率是有用的。pseudo probability的计算公式如下:
（4）
我们可以看到跟传统的n-gram公式相比，它的分子多减去一项，被减去的这一项也就是
第五步计算得到的discount。
接下来我以**u(我)和u(我∣你)**为例来详细介绍下计算过程，其他概率的计算读者有兴趣的话可以自己做下。

• 对于u(我)的计算，n=1;

$a(我)=\frac{a(我)-D_n(a(我))}{{\Sigma }_{x}a(x)}=\frac{1-1/2}{1+1}$

其中${\Sigma }_{x}a(x)$ = a(我) + a(你) + a(他) + a(<\s>) = 2+1+1+3 = 7。需要注意的是我们并没有加上a()，因为最为句子开头标志，其前面不可能再有其他词。

• 对于u(我|你)的计算，n=2;

$a(我|你)=\frac{a(我|你)-D_n(a(我|你))}{{\Sigma }_{x}a(你x)}=\frac{2-1/2}{2+1+1+3}$

其中${\Sigma }_{x}a(你x)$ = a(你 我) + a(你 ) = 1+1 = 2。

② 计算回退权重，也称为back-off weight, 它衡量的是某个词后面能接不同词的能力。举个例子，考虑 spite 和 constant 的 bigram，在 Europarl corpus 中，两个 bigram 都出现了 993 次，以 spite 开始的 bigram 只有 9 种，大多数情况下 spite 后面跟着 of(979 次)，因为 in spite of 是常见的表达，而跟在 constant 后的单词有 415 种，所以我们更有可能见到一个跟在 constant 后面的bigram，因此back-off(constant)>back-off(spite)。 基于上述思想，定义其表达式为:
(5)
根据该公式，再结合表3和表6，我们可以计算每个字的回退权重，如下：
$b(你)=\frac{\frac{1}{2}\ast 2+\frac{5}{4}\ast 0+3\ast 0}{2}=\frac{1}{2}$

$b(我)=\frac{\frac{1}{2}\ast 0+\frac{5}{4}\ast 0+3\ast 1}{3}=1$

$b(他)=\frac{\frac{1}{2}\ast 1+\frac{5}{4}\ast 0+3\ast 0}{1}=\frac{1}{2}$

$b(<s>)=\frac{\frac{1}{2}\ast 1+\frac{5}{4}\ast 2+3\ast 0}{5}=\frac{3}{5}$

然后对上述的概率取以10为底的log，就能得到与图1中的第三列对应的结果。需要注意的是我们没有计算b()，这是因为已经是句子的最后一个单词，它在后退之后就没有其他词了。
ps：arpa中的概率是取log10，而不是ln!

七、Interpolation。在讲解Interpolation之前，我们先看一个例子:如果c(多的)和c(多敛) 都为0，也就是说在某个语料中都没出现，那么在传统的n-gram中，p(的∣多)=p(敛∣ 多)。而这个概率我们直观上来看是错误的，p(的∣多)应该比p(敛∣多)高很多。要实 现这个，我们就希望把 bigram 和 unigram 结合起来，因为“的”比“敛”常见的多，就能保证p(的∣多)>p(敛∣多)。interpolate 就是这样一种方法，它的数学表达式如下所示:

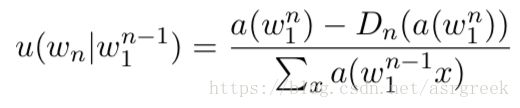(6)
该过程不断递归，直到unigram停止。其中unigram的插值用uniform distribution表 示，如下列表达式所示:
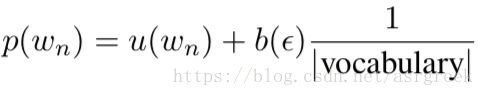(7)
其中$\left|vocabulary\right|$表示词汇量大小，这里总共有{、我、你、他、<\s>}5个词，所以 $\left|vocabulary\right|$ =5；ε表示空字符串。$b\left(\epsilon \right)$的计算需要特别说明下：

$b\left(\epsilon \right)=\frac{\frac{1}{2}\ast 2+\frac{1}{2}\ast 1+3\ast 1}{2+1+1+3}=\frac{9}{14}$

需要注意的是，上式对于$b\left(\epsilon \right)$的计算，n应该取1。
接下来我们选取几个概率进行计算，来验证下计算结果是否与实际结果相同。

$p(我)=u(我)+b\left(\epsilon \right)\ast \frac{1}{|vocabulary|}=\frac{3}{14}+\frac{9}{14}\ast \frac{1}{5}=\frac{24}{70}$

$p(我|你)=u(我|你)+b(你)\ast p(我)=\frac{1}{4}+\frac{1}{2}\ast \frac{24}{70}\approx 0.4214285$

如果你仔细看图1，你会发现其中有个字符，但实际上我们的文本中并没有这个字符。引入字符后，我们就可以把未登录词当作对待。
因为我们这个例子没有未登录词，所以字符的计数为0，即a()=0。

$p(<unk>)=0+b\left(\epsilon \right)\ast \frac{1}{|vocabulary|}=\frac{9}{14}\ast \frac{1}{5}=\frac{9}{70}$

同样的，对上述的概率取以10为底的log，就能得到与图1中的第一列对应的结果。 因为篇幅有限(实际上也没这个必要)，我就不把全部的概率计算过程列出来了。读者 有兴趣可以按照上面的方法把全部概率都计算一遍，再跟实际结果对比。

希望这个简单的例子对大家理解n-gram和Modified Kneser-ney smoothing有所帮助，谢谢!

---

[1]: Heafield K, Pouzyrevsky I, Clark J H, et al. Scalable Modified Kneser-Ney Language Model Estimation[C]// Meeting of the Association for Computational Linguistics. 2013:690-696.