贪心算法介绍及区间调度问题

一、基本概念：

 

     所谓贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。

     贪心算法没有固定的算法框架，算法设计的关键是贪心策略的选择。必须注意的是，贪心算法不是对所有问题都能得到整体最优解，选择的贪心策略必须具备无后效性，即某个状态以后的过程不会影响以前的状态，只与当前状态有关。

    所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。

 

二、贪心算法的基本思路：

    1.建立数学模型来描述问题。

    2.把求解的问题分成若干个子问题。

    3.对每一子问题求解，得到子问题的局部最优解。

    4.把子问题的解局部最优解合成原来解问题的一个解。

 

三、贪心算法适用的问题

      贪心策略适用的前提是：局部最优策略能导致产生全局最优解。

    实际上，贪心算法适用的情况很少。一般，对一个问题分析是否适用于贪心算法，可以先选择该问题下的几个实际数据进行分析，就可做出判断。

 

四、贪心算法的实现框架

    从问题的某一初始解出发；

    while （能朝给定总目标前进一步）

    { 

          利用可行的决策，求出可行解的一个解元素；

    }

    由所有解元素组合成问题的一个可行解；

 

五、贪心算法之区间调度问题

解题分析：

对这个问题，如果使用贪心算法，有以下几种考虑：

（1）每次选取开始时间最早的；

（2）每次选取结束时间最早的；

（3）每次选取用时最短的；

（4）在可选工作中，每次选取与最小可选工作有重叠的部分；

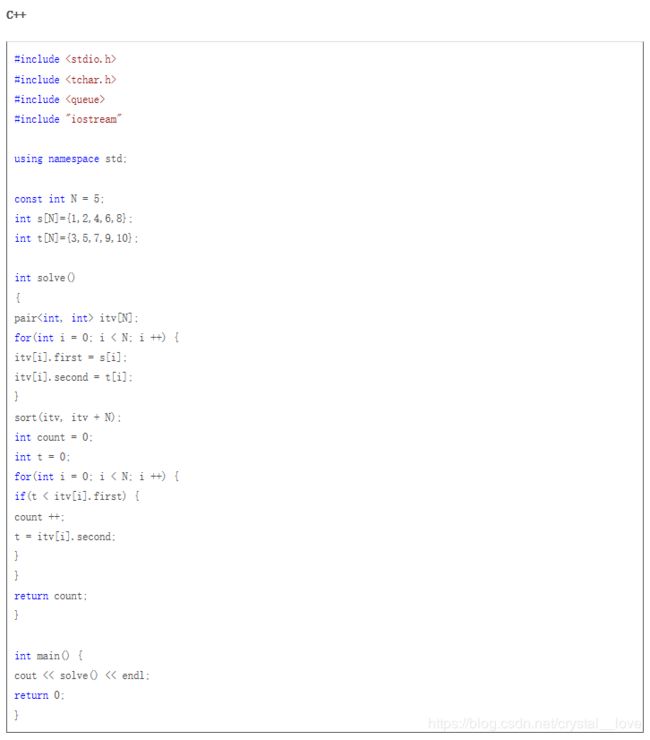
如果要选出最多的区间，则应该用第二种思路，C++代码如下：

（一）单区间调度问题

问题定义：存在单一资源，有一组以时间区间形式表示的资源请求reqs={req-1, req-2, …, req-n}，第i个请求希望占用资源一段时间来完成某些任务，这段时间开始于begin(i)终止于end(i)。如果两个请求req-i和req-j在时间区间上没有重叠，则说这两个请求是相容的，求出这组请求的最大相容子集(最优子集)。举个例子：有一间多媒体课室，某一个周末有多个社团想要申请这间课室去举办社团活动，每个社团都有一个对应的申请时间段，比如周六上午8:00-10:00。求出这间课室在这个周末最多能满足几个社团的需求。

解决方案：贪心算法，优先选择最早结束的需求，确保资源尽可能早地被释放，把留下来满足其他需求的时间最大化。具体伪代码如下所示，算法结束后集合A中会保留所有相容请求，A的大小即是最大相容数量。

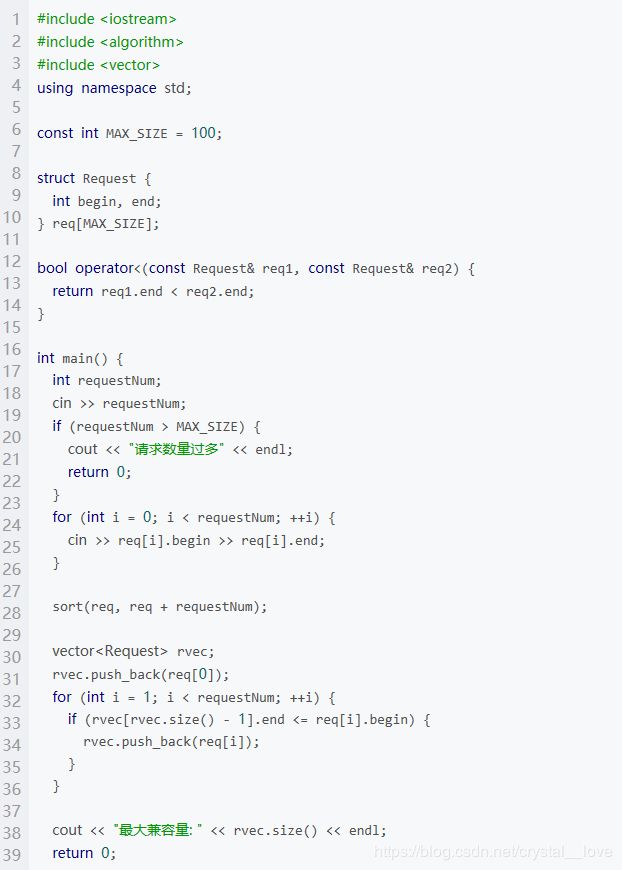
（二）多区间调度问题

问题定义：存在多个(或者无限多个)相同的资源，有一组以时间区间形式表示的资源请求reqs={req-1, req-2, …, req-n}，第i个请求希望占用资源一段时间来完成某些任务，这段时间开始于begin(i)终止于end(i)。如果两个请求req-i和req-j在时间区间上没有重叠，则说这两个请求是相容的，用尽可能少的资源满足所有请求(求最优资源数量)。举个例子：有很多间课室，某个周末有多个社团需要申请课室办活动，每个社团都有一个对应的申请时间，求最少需要多少间课室才能够满足所有社团的需求(在这个问题之中时间重叠的社团需要安排在其他课室，即会使用到多个资源，需要考虑多个资源上的调度安排，故称为多区间调度)。

解决方案：贪心算法，将需求按照开始时间的早晚进行排序，然后开始为这些资源打标签，每个标签代表都一个资源，需求req-i被打上标签k表示该请求分配到的资源是k。遍历排序后的需求，如果一个需求与某个已分配资源上的其他安排不冲突，则把该需求也放进该资源的安排考虑中；如果冲突，那么应该要给此需求分配新的资源，已用资源数量加一。具体操作的伪代码如下所示。

C++代码如下：

#include
#include
#include
using namespace std;

const int MAX_SIZE = 100;

struct Request {
  int begin, end, tag;
} req[MAX_SIZE];

bool operator<(const Request& req1, const Request& req2) {
  return req1.begin < req2.begin;
}

int main() {
  int requestNum;
  cin >> requestNum;
  if (requestNum > MAX_SIZE) {
    cout << "请求数量过多" << endl;
    return 0;
  }
  for (int i = 0; i < requestNum; ++i) {
    cin >> req[i].begin >> req[i].end;
  }

  sort(req, req + requestNum);

  int tagSize = 1;
  req[0].tag = 0;
  bool tags[MAX_SIZE];
  for (int i = 1; i < requestNum; ++i) {
    memset(tags, 1, sizeof(tags));
    for (int j = 0; j < i; ++j) {
      if (req[j].end > req[i].begin) {
        tags[req[j].tag] = false;
      }
    }
    bool isTagsEmpty = true;
    int tag;
    for (int j = 0; j < tagSize; ++j) {
      if (tags[j]) {
        isTagsEmpty = false;
        tag = j;
        break;
      }
    }
    if (isTagsEmpty) {
      req[i].tag = tagSize;
      ++tagSize;
    } else {
      req[i].tag = tag;
    }
  }

  cout << "最小资源使用量: " << tagSize << endl;
  return 0;
}
 

（三）最小延迟调度问题

问题定义：存在单一资源和一组资源请求reqs={req-1, req-2, …, req-n}，与前面两个问题不同，这里的资源从时刻0开始有效(开始接受申请，开始可以被使用)，每个请求req-i都有一个截止时间ddl(i)，每个请求都要占用资源一段连续的时间来完成任务，占用时间为time(i)。每个请求都希望自己能在ddl之前完成任务，不同需求必须被分在不重叠的时间区间(单一资源，同一时刻只能满足一个请求)。假设我们计划满足每个请求，但是允许某些请求延迟(即某个请求在ddl之后完成，延误工期)，确定一种合理的安排，使得所有请求的延期时间中的最大值，是所有可能的时间安排情况中最小的。从时刻0开始，为每个请求req-i分配一个长度time(i)的时间区间，把区间标记为[begin(i), end(i)]，其中end(i) = begin(i) + time(i)。如果end(i) > ddl(i)，则请求req-i被延迟，延迟时间为delay(i) = end(i) - ddl(i)；否则delay(i) = 0。合理安排需求，使得maxDelay = max{delay(1), delay(2), …, delay(n)}是所有可能的安排中最小的。

解决方案：贪心算法，按照截止时间ddl排序，越早截止的任务越早完成。该算法是一个没有空闲的最优调度，即从时刻0开始都有在处理请求，直到最后一个请求执行完释放资源之后才空闲。伪代码如下所示。

C++代码如下：

#include
#include
using namespace std;

const int MAX_SIZE = 100;

struct Request {
  int time, ddl;
  int begin, end;
} req[MAX_SIZE];

bool operator<(const Request& req1, const Request& req2) {
  return req1.ddl < req2.ddl;
}

int main() {
  int requestNum;
  cin >> requestNum;
  if (requestNum > MAX_SIZE) {
    cout << "请求数量过多" << endl;
    return 0;
  }
  for (int i = 0; i < requestNum; ++i) {
    cin >> req[i].time >> req[i].ddl;
  }

  sort(req, req + requestNum);

  int start = 0, maxDelay = 0;
  for (int i = 0; i < requestNum; ++i) {
    req[i].begin = start;
    req[i].end = start + req[i].time;
    start += req[i].time;
    if (maxDelay < req[i].end - req[i].ddl) {
      maxDelay = req[i].end - req[i].ddl;
    }
  }

  cout << "最小的最大延迟: " << maxDelay << endl;
  return 0;
}