信息检索导论读书笔记（六）：文档评分、词项权重计算及向量空间模型
在文档集规模很大的情况下，满足布尔查询的结果文档数量可能非常多，往往会大大超过用户能够浏览的文档数目。因此对搜索引擎来说，对文档进行评分和排序非常重要。
参数化索引及域索引
大多数文档具有额外的结构信息，与文档相关的特定形式的数据（比如作者、标题、出版日期等）我们称为元数据。数字文档通常会把与之相关的元数据以机读的方式一起编码。元数据通常会包括字段信息，对每个字段（比如文档创建时间）建立与之对应的参数化索引，通过它我们只选择在字段上满足查询需求的文档。对字段的词典采用类似B树的数据结构进行组织。
域与字段很相似，字段通常的取值可能性相对较小，域的内容可以是任意的自由文本。比如，通常可以把文档的标题和摘要看做域，然后对文档不同的域构建独立的倒排索引，用以支持类似“寻找标题中出现xxx”之类的查询请求。
参数化索引中，词典常常来自固定的词汇表（比如语言种类、日期），域索引中，词典中应该收集来自域中自由文本的所有词汇。
域加权评分：
给定一个布尔查询 q 和一篇文档 d ，域加权评分方法给查询词 q 与文档 d 中的每个月匹配度进行加权计算，从而获得最终评分，假设文档有 
个域，域加权评分方法可以定义为： 
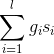。该方法有时也称为排序式布尔检索。
实际操作中，在进行布尔查询操作时，对满足查询条件的文档计算域加权评分即可。当然如果评分设计更复杂也可以实现不满足所有查询条件（即部分满足查询条件）的文档也得到非零评分。
权重学习：
进行域加权评分过程中，非常重要的一部分是不同域的权重，如何确定每个域的权重？权重可以由专家甚至普通用户指定，但是现在越来越倾向于使用机器学习的方式，使用人工标注好的数据进行训练，确定评分及排序。
词项频率及权重计算
在此之前只考虑了词项在文档域中出现与否两种情况。进一步的我们还可以考虑词项在文档或域中出现的频率。
对于在搜索界面上自由输入的简单查询，一种合理的查询方式是将查询看成多个词的组合，可以基于每个查询词项与文档的匹配情况对文档打分，然后对文档与所有查询词项的匹配得分求和。此时我们可以对文档中每个词项赋予一个权重，它取决于词项在文档中出现的次数。
对于词项 t ，根据其在文档 d 中的权重来计算它的得分。最简单的方式是将权重设置为文档中的出现次数，这种权重计算的结果称为词项频率。对于文档 d ，所有词项的词项频率的集合我们称为词袋模型。在词袋模型中，词项出现的次序被忽略，只关心出现的次数。
逆文档频率：
文档中不同的词项的重要性是不一样的，某些词项对于相关度计算来说几乎没有区分能力，为此我们需要降低这些出现次数很多但是区分能力很低的词项的重要性。一种直接的思路就是给文档集频率（cf）较高的词项赋予较低的权重。实际中，更常用的是文档频率（df），而非文档集频率。因为我们想要的是区分不同的文档，所以应该采用文档粒度上的统计，而不是文档集。下图中是两个单词的文档集频率与文档频率，他们的文档集频率基本相等，但是insurance的文档频率远低于try，也就是说集中在更少的文档中，所以显然应该给insurance更高的权重。
因为 df 本身往往较大，所以通常需要将它映射到一个较小的取值范围中，因此提出了逆文档频率：
。其中N为文档数。根据这个计算公式，一个罕见词的 idf 往往很高，而高频词的 idf 可能很低。
tf-idf权重计算：
对于每篇文档中的每个词项，可以将其 tf（词项在文档中出现的频率） 和 idf（词项逆文档频率） 组合在一起形成最终的权重： 
。也就是说最终词项 t 在文档 d 中的权重与词项 t 在文档中出现频率成正比，与逆文档频率成正比。在这种模型下：
- 当 t 在少数几篇文档中多次出现时，其权重最大
- 当 t 在一些文档中出现次数很少，或者在很多文档中出现，权重取值次之
- 当 t 在所有文档中都出现，权重值最小
向量空间模型
通过 tf-idf权重计算可以计算每篇文档中所有词项的权重，这样就可以将文档看成一个向量，其中每个分量都对应一个词项，分量值为权重值。这种向量形式对于评分和排序十分重要。而一系列文档在同一向量空间中的表示被称为向量空间模型（vector space model），它是信息检索领域文档评分、分类及聚类等相关处理的基础。在使用向量空间模型评分时，其中很关键的一步是将查询也看成同一空间下的向量。
余弦相似度：
一组文档的集合可以看成向量空间中的多个向量，每个词项对应一个坐标轴。当我们想对两篇文档相似度进行计算时，一种方式是计算两个文档向量的差向量，但由于两篇文档的长度可能不同，导致文档向量长度相差较大。因此往往不比对向量长度，而是比较向量的方向即可，这可以通过计算余弦相似度实现：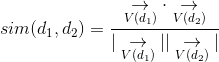
。其中分子是两个文档向量的内积，分母是两向量的欧几里得长度乘积。余弦相似度值越大的文档相似度越高。
查询向量：
我们将查询看成词袋，那么就可以将查询当成一篇极短的文档来表示成向量，进而通过计算查询向量与文档向量的余弦相似度来对所有文档进行排名。这样即使一篇文档不包含所有的查询词项也可能会获得较高的余弦得分。
总结下来，整个检索过程就是：计算查询向量和文档集中每个文档向量的余弦相似度，结果按照得分排序，并选择得分最高的 K 篇文档。实际这个过程的代价很大，因为每次相似度计算都是数万维向量之间的内积计算，具体计算方法后续进行讨论，此处不再展开。