机器学习-逻辑回归总结
分类问题
与线性回归不同,Logistic回归虽然带有"回归"二字,但是并不是回归问题,属于分类问题。简单介绍一下,什么是分类问题。
在监督学习中,当输出变量Y取有限个离散值时,预测问题便成为分类问题。这时,输入变量X可以是离散的,也可以是连续的。
监督学习从数据中学习一个分类模型或分类决策函数,称为分类器。分类器对新的输入进行输出的预测,称为分类。可能的输出称为类。分类的类别为两个时,称为二分类问题;分类的类别为多个时,称为多类分类问题。
举个例子,经典的二分类,比如检查邮件是否是垃圾邮件,检查一个零件是否是合格件,判断一个西瓜是否成熟等等。对于类别我们通常称为正类(positive class)和负类(negative class),垃圾邮件的例子中,正类就是正常邮件,负类就是垃圾邮件。
逻辑回归常用于二分类问题,也可以用于多分类问题,后面会有介绍。逻辑回归与线性回归虽然是两个不同的问题,但是两者还是有一些相似之处,我们可以建立在对线性回归理解的基础上,来对比学习逻辑回归。
逻辑回归模型
逻辑回归和线性回归等回归任务还是有一定关系的,这种关系正是通过一种神奇的映射曲线做到的,比如它将做回归分析的模型的因变量的取值映射为概率值,我们都知道概率值的取值范围为0~1,所以通过设定一个0~1的阈值,小于这个阈值的就是A类,其他的都是非A类,这就是二分类。
模型描述
首先,我们先介绍我们上面提到的那个神奇的映射函数,我们称之为Sigmoid函数:
g ( z ) = 1 1 + e − z g\left( z\right) =\dfrac {1}{1+e^{-z}} g(z)=1+e−z1
可以看出该函数定义域为实数域R,值域为(0,1)。
函数图像如下:

因为该函数的取值范围为R,所以我们可以把z用任何一个函数式替换,既形成一个复合函数,这就意味着这个函数可以作为任何函数关系的映射函数。并且该函数的值域为(0,1),很好满足概率值为0-1的特性。
我们再对该函数求导,看看该函数的另一个特性:
g ′ ( z ) = 1 ( 1 + e − z ) 2 e − z = 1 1 + e − z ⋅ e − z 1 + e − z = g ( z ) ( 1 − g ( z ) ) \begin{aligned}g'\left( z\right) =\dfrac {1}{\left( 1+e^{-z}\right) ^{2}}e^{-z}\\ =\dfrac {1}{1+e^{-z}}\cdot \dfrac {e^{-z}}{1+e^{-z}}\\ =g\left( z\right) \left( 1-g\left( z\right) \right) \end{aligned} g′(z)=(1+e−z)21e−z=1+e−z1⋅1+e−ze−z=g(z)(1−g(z))
此函数应用甚广,神经网络的激励函数,独立成分分析中源信号分布都是使用该函数的。
接下来介绍逻辑回归的假设函数:
h θ ( x ) = 1 1 + e − θ T x h_{\theta }\left( x\right) =\dfrac {1}{1+e^{-\theta^{T} x}} hθ(x)=1+e−θTx1
我们可以看到,我们用 θ T x \theta^{T} x θTx代替了映射函数里的z。
θ T x \theta^{T} x θTx是不是有一点眼熟呢?没错,我们在线性回归中见到过,线性回归的表达式可以用 θ T x \theta^{T} x θTx来表示。
需要注意的是,这里的 θ T x \theta^{T} x θTx既可以是线性的关系,也可以是非线性的关系。
比如:
假设函数可以是: h θ ( x ) = g ( θ 0 + θ x 1 + θ 2 x 2 ) h_{\theta }\left( x\right) =g\left( \theta _{0}+\theta x_1+\theta _{2}x_2\right) hθ(x)=g(θ0+θx1+θ2x2)
也可以是: h θ ( x ) = g ( θ 0 + θ x 1 2 + θ 2 x 2 3 ) h_{\theta }\left( x\right) =g\left( \theta _{0}+\theta x_1^{2}+\theta _{2}x_2^{3}\right) hθ(x)=g(θ0+θx12+θ2x23)
假设2个类分别为0和1,回归结果hθ(x)表示样本属于类1的概率,因此样本属于类0的概率则为1−hθ(x),则有:
P ( y = 1 ∣ x , θ ) = h θ ( x ) P( y= 1|x,\theta ) =h_{\theta }\left( x\right) P(y=1∣x,θ)=hθ(x)
P ( y = 0 ∣ x , θ ) = 1 − h θ ( x ) P( y= 0|x,\theta ) =1-h_{\theta }\left( x\right) P(y=0∣x,θ)=1−hθ(x)
实际上就是一个两点分布,可写为 P ( y ∣ x , θ ) = h θ y ( x ) ( 1 − h θ ( x ) ) 1 − y P( y|x,\theta ) =h_{\theta }^{y}\left( x\right)(1-h_{\theta }\left( x\right))^{1-y} P(y∣x,θ)=hθy(x)(1−hθ(x))1−y
通常在做二分类时,设定一个阈值 gamma,如果小于gamma,设为 0类,否则为 1类。阈值是可以调整的,比如说一个比较保守的人,可能将阈值设为0.9,也就是说有超过90%的把握,才相信这个x属于1这一类。如下图所示:设定阈值为0.3,则小于0.3的都为 0 类,大于0.3的都为 1 类。
决策界限
线性的决策边界,如下图:

解释一下图中的情况,我们假设 θ T x \theta^{T} x θTx=-3+x1+x2。将阈值设为0.5,即当 h θ ( x ) h_{\theta }\left( x\right) hθ(x)>0.5时,我们认为属于正类,否则,属于负类,由映射函数g(z)可知,当z=0时,g(z)=0.5,所以也就是当 θ T x \theta^{T} x θTx>0时,即-3+x1+x2>0时,属于正类,y=1。所以,此时的决策界限就是一条直线,如上图所示,该直线下部分属于y=0,上部分为y=1。
代价函数
线性回归中的代价函数用的是平方和的代价函数,但是在逻辑回归的问题中,如果仍然使用平方和代价函数的话,很有可能此时的代价函数是非凸函数,即有很多局部最优点,如果此时用梯度下降法,不能保证会收敛到全局最小值。
所以,逻辑回归的代价函数我们使用交叉熵作为代价函数: J ( θ ) = − 1 m [ ∑ i = 1 m ( y ( i ) log h θ ( x ( i ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = -\frac{ 1 }{ m }[\sum_{ i=1 }^{ m } ({y^{(i)} \log h_\theta(x^{(i)}) + (1-y^{(i)}) \log (1-h_\theta(x^{(i)})})] J(θ)=−m1[i=1∑m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
m:训练样本的个数;
hθ(x):用参数θ和x预测出来的y值;
y:原训练样本中的y值,也就是标准答案
上角标(i):第i个样本
这个代价函数其实也是由最大似然法推出的,我们在这里就不证明了。
所以,此时我们的目标就成了寻找最优的 θ \theta θ使得 J ( θ ) J(\theta) J(θ)的值最小。
我们仍然使用的是梯度下降算法。
梯度下降
将 ∂ ∂ θ j J ( θ ) \dfrac {\partial }{\partial \theta _{j}}J\left( \theta \right) ∂θj∂J(θ)代入可得:
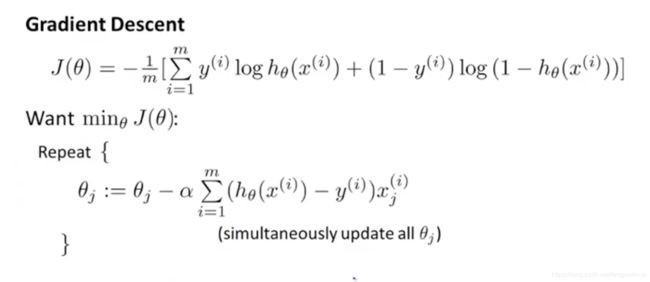
我们会惊讶的发现,逻辑回归得到的梯度下降的式子跟线性回归的式子形式结果是一样的,但是需要注意的是,这里的函数 h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i))并不一样。
多分类问题
逻辑回归虽然主要用于二分类问题,但是也可以用于多分类问题。
思路是将多分类问题转换成多个二分类问题
对每一个类训练一个逻辑回归模型,有多少个类就有多少个模型
用每一个模型对新数据分别进行预测,取概率最大的模型决定新数据的预测类别。


