【FFT】快速傅里叶变换详解
傅里叶变换历史
傅里叶是一位法国数学家和物理学家的名字,英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣,于1807年在法国科学学会上发表了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断:任何连续周期信号可以由一组适当的正弦曲线组合而成。当时审查这个论文的人,其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其它审查者投票通过并要发表这个论文时,拉格朗日坚决反对,在他此后生命的六年中,拉格朗日坚持认为傅里叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望,拒绝了傅里叶的工作,幸运的是,傅里叶还有其它事情可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。
拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号。但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅里叶是对的。
用正弦曲线来代替原来的曲线而不用方波或三角波来表示的原因在于,分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示
天才在左 疯子在右
由于傅里叶极度痴迷热学,他认为热能包治百病,于是在一个夏天,他关上了家中的门窗,穿上厚厚的衣服,坐在火炉边,结果因CO中毒不幸身亡,1830年5月16日卒于法国巴黎。
多项式
一个以x为变量的多项式定义在一个代数域F上,将函数A(x)表示为形式和:
次数界
如果一个多项式![]() 的最高次的非零系数是
的最高次的非零系数是![]() ,则称
,则称![]() 的次数是k,记 degree(A) = k。 任何严格大于一个多项式次数的整数都是该多项式的次数界
的次数是k,记 degree(A) = k。 任何严格大于一个多项式次数的整数都是该多项式的次数界
多项式加法
如果![]() 和
和![]() 是次数界为n的多项式,那么它们的和也是一个次数界为n的多项式
是次数界为n的多项式,那么它们的和也是一个次数界为n的多项式
多项式乘法
如果![]() 和
和![]() 是次数界为n的多项式,它们的乘积是一个次数界为2n-1的多项式
是次数界为n的多项式,它们的乘积是一个次数界为2n-1的多项式
多项式的表示
系数表达
一个次数界为n的多项式  而言,其系数表达是一个由系数组成的向量
而言,其系数表达是一个由系数组成的向量![]()
霍纳法则
![]()
![]() 时间复杂度内计算
时间复杂度内计算![]()
卷积(convolution)
系数向量c称为输入向量a和b的卷积
点值表达
一个次数界为n的多项式A(x)的点值表达就是一个由n个点值对所组成的集合
![]()
使得对 k = 0, 1, 2, ... , n-1, 所有![]() 各不相同,
各不相同, ![]()
插值
从一个多项式的点值表达确定其系数表达形式
插值多项式的唯一性
对于任意n个点值对组成的集合![]() ,其中所有的
,其中所有的![]() 都不同;那么存在唯一的次数界为n的多项式
都不同;那么存在唯一的次数界为n的多项式![]() ,满足
,满足![]()
![]()
范德蒙德矩阵![]() ,也就是左边的矩阵,该矩阵行列式的值为
,也就是左边的矩阵,该矩阵行列式的值为 ![]() (数学归纳法)
(数学归纳法)
如果![]() 都不同,则该矩阵是可逆的(非奇异的),行列式的值不为0
都不同,则该矩阵是可逆的(非奇异的),行列式的值不为0
![]()
LU分解算法可以在![]() 的时间复杂度内求出方程的解
的时间复杂度内求出方程的解
拉格朗日插值法
对拉格朗日插值法感兴趣的童鞋可以参考笔者的博客:https://blog.csdn.net/giftedpanda/article/details/99621691
2n个点值对的缘由:为了保证插值的唯一性
![]() ,则
,则 ![]() ,对A的点值表达和B的点值表达进行逐点相乘,就可以得到C的点值表达。但是degree(C) = degree(A) + degree(B)。如果A和B的次数界都为n,那么C的次数界为2n。A和B多项式的点值表达都由n个点值对组成,当我们把这些点值对相乘时,就得到C的n个点值对,由于C的次数界为2n,要插值获得唯一的多项式,我们需要2n个点值对。
,对A的点值表达和B的点值表达进行逐点相乘,就可以得到C的点值表达。但是degree(C) = degree(A) + degree(B)。如果A和B的次数界都为n,那么C的次数界为2n。A和B多项式的点值表达都由n个点值对组成,当我们把这些点值对相乘时,就得到C的n个点值对,由于C的次数界为2n,要插值获得唯一的多项式,我们需要2n个点值对。
单位复数根
n次单位复数根
满足 ![]() 的复数
的复数 ![]() , n次单位复数根恰好有n个,
, n次单位复数根恰好有n个, ![]() =
= ![]() , k = 0, 1, ..., n - 1
, k = 0, 1, ..., n - 1
n个单位复数根均匀地分布在以复平面的原点为圆心的单位半径的圆周上![]()
主n次单位根
![]() ,所有其他n次单位复数根都是
,所有其他n次单位复数根都是![]() 的幂次
的幂次
n个n次单位复数根![]() 在乘法意义下形成一个群,
在乘法意义下形成一个群,![]()
消去引理
对任何整数 n ![]() 0, k
0, k ![]() 0, 以及d > 0,
0, 以及d > 0, ![]()
证明
![]()
折半引理
如果n > 0 为偶数,那么n个n次单位复数根的平方的集合就是n/2个n/2次单位复数根的集合
证明
![]()
求和引理
对任意整数n ![]() 1和不能被n整除的非负整数k有
1和不能被n整除的非负整数k有
证明
DFT
我们计算次数界为n的多项式
在![]() 处的取值得到 n 个点值对
处的取值得到 n 个点值对![]()
向量![]() 就是系数向量
就是系数向量![]() 的离散傅里叶变换(DFT)
的离散傅里叶变换(DFT)
FFT:快速傅里叶变换
FFT采用分治策略,采用A(x)中偶数下标的系数和奇数下标的系数,分别定义两个新的次数界为n/2的多项式![]() 和
和![]()
![]()
![]()
![]() 包含A中所有偶数下标的系数(下标的相应二进制表达的最后一位为0),以及
包含A中所有偶数下标的系数(下标的相应二进制表达的最后一位为0),以及![]() 包含A中所有奇数下标的系数(下标的相应二进制表达的最后一位为1)。
包含A中所有奇数下标的系数(下标的相应二进制表达的最后一位为1)。
![]()
所以求![]() 在
在![]() 处的值的问题转换为求次数界为n/2的多项式
处的值的问题转换为求次数界为n/2的多项式![]() 和
和![]() 在点
在点![]() 的取值。因此我们可以递归地对次数界为n/2的多项式
的取值。因此我们可以递归地对次数界为n/2的多项式![]() 和
和![]() 在n/2个n/2次单位复数根出求值。
在n/2个n/2次单位复数根出求值。
一个元素的DFT就是该元素自身
![]()
![]()
在单位复数根处插值
我们把DFT写成矩阵乘积![]() ,其中
,其中![]() 是一个由
是一个由![]() 适当幂次填充成的范德蒙德矩阵
适当幂次填充成的范德蒙德矩阵
对于j, k = 0, 1, ..., n -1, ![]() 的 (k, j) 处元素为
的 (k, j) 处元素为![]() ,
, ![]()
对j , k = 0, 1, ..., n-1, ![]() 的(j, k)处元素为
的(j, k)处元素为![]()
证明
![]() ,其中
,其中![]() 为n × n的单位矩阵,考虑
为n × n的单位矩阵,考虑![]() 中
中![]() 的元素:
的元素:
如果![]() ,此和为1,否则,此和为0。
,此和为1,否则,此和为0。
可以推导出![]() ,离散傅里叶逆变换 (IDFT)
,离散傅里叶逆变换 (IDFT)
对FFT算法进行如下修改就可以计算出IDFT:把a与y互换,用![]() 替换
替换![]() ,并将计算结果的每个元素除以n。
,并将计算结果的每个元素除以n。
卷积定理
对任意两个长度为n的向量a和b,其中n是2的幂,
![]()
其中向量a和b用0填充,使其长度达到2n,并用“·”表示2个2n个元素组成的向量点乘
高效FFT实现
![]()
![]()
在上面两个等式中,我们对 ![]() 进行了两次计算,在编译术语中,称该值为公用因子表达式。
进行了两次计算,在编译术语中,称该值为公用因子表达式。
我们把![]() 的值存进临时变量中,然后从
的值存进临时变量中,然后从![]() 中增加及减去这个临时变量,这一系列操作称为一个蝴蝶操作
中增加及减去这个临时变量,这一系列操作称为一个蝴蝶操作
蝴蝶操作图解
FFT的迭代结构实现
位逆序置换
我们前面分治时,将元素按奇偶下标分组,假设我们现在有8个元素
未分组前: |0 1 2 3 4 5 6 7|
第一次分组后: |0 2 4 6| |1 3 5 7|
第二次分组后: |0 4| |2 6| |1 5| |3 7|
第三次分组后: |0| |4| |2| |6| |1| |5| |3| |7|
然后你会惊奇的发现,哦,你没发现,那我告诉你吧,
每个元素最后出现的位置为该元素相应二进制的逆序,如4的二进制逆序为001,所以出现在了第一个位置。
我们通过这个结论,就可以将自顶向下的递归实现优化为自底向上的迭代实现。
首先,我们成对取出元素,利用一次蝴蝶操作计算出每对的DFT,然后用其DFT取代这对元素。这样向量中就包含了n/2个二元素的DFT。下一步,我们按对取出这n/2个DFT,通过两次蝴蝶操作计算出具有四个元素向量的DFT,并用一个具有四元素的DFT取代对应的两个二元素的DFT。于是向量中包含n/4个四元素的DFT。继续进行这一过程,直至向量中包含两个具有n/2个元素的DFT,这时,我们综合应用n/2次蝴蝶操作,就可以合成具有n个元素的DFT。
至此,我们已经学完了FFT所需要的全部知识了。开心吧!!!
给定FFT,我们就有下面时间复杂度为![]() 的方法,该方法把两个次数界为n的多项式A(x)和B(x)进行乘法运算,其中输入与输出均采用系数表达。假设n是2的幂。实际上,我们可以通过添加系数为0的高阶系数,来满足这个要求。
的方法,该方法把两个次数界为n的多项式A(x)和B(x)进行乘法运算,其中输入与输出均采用系数表达。假设n是2的幂。实际上,我们可以通过添加系数为0的高阶系数,来满足这个要求。
1. 加倍次数界:通过加入n的系数为0的高阶系数,把多项式A(x)和B(x)变为次数界为2n的多项式,并构造其系数表达。
2. 求值: 通过应用2阶FFT计算出A(x)和B(x)的长度为2n的点值表达。这些点值表达中包含了两个多项式在2n次单位根的取值。
3. 逐点相乘: 把A(x)的值与B(x)的值逐点相乘,可以计算出多项式C(x) = A(x)B(x)的点值表达,这个表示中包含了C(x)在每个2n次单位根处的取值。
4. 插值:通过对2n的点值对应用FFT,计算其逆DFT,就可以构造出C(x)的系数表达。
FFT模板代码
#include
#include
#include
#include
#include
using namespace std;
typedef complex cp;
const double pi = acos(-1);
const int maxn = 200000 + 8;
char sa[maxn], sb[maxn];
int n, lena, lenb, res[200000+8];
cp a[maxn], b[maxn], omg[maxn], inv[maxn]; // omg 单位根 inv 单位根的共轭
void init() // 初始化
{
memset(omg, 0, sizeof(omg));
memset(inv, 0, sizeof(inv));
for(int i = 0; i < n; i++) {
omg[i] = cp(cos(2 * pi * i / n), sin(2 * pi * i / n));
inv[i] = conj(omg[i]);
}
memset(res, 0, sizeof(res));
memset(a, 0, sizeof(a));
memset(b, 0, sizeof(b));
}
void FFT(cp *a, cp *omg) // 快速傅里叶变换
{ int lim = 0;
while((1 << lim) < n) lim++; // 确定位数
for(int i = 0; i < n; i++) { // 确定最后的位置
int t = 0;
for(int j = 0; j < lim; j++) // 枚举每一位是否为1 然后变换
if((i >> j) & 1) t |= (1 << (lim - j - 1)); // 确定分组的最后位置
if(i < t) swap(a[i], a[t]); // i < t 的限制使得每对点只被交换一次(否则交换两次相当于没交换)
}
for(int l = 2; l <= n; l *= 2) { // 分治 向上还原
int m = l / 2;
for(cp *p = a; p != a + n; p += l)
for(int i = 0; i < m; i++) {
cp t = omg[n / l * i] * p[i + m]; // 蝴蝶操作
p[i + m] = p[i] - t;
p[i] += t;
}
}
}
int main()
{
while(scanf("%s %s", sa, sb) == 2) {
lena = strlen(sa), lenb = strlen(sb);
n = 1;
while(n < lena + lenb) n *= 2; // 补齐位数
init(); // 初始化
for(int i = 0; i < lena; i++) // 实部初始化
a[i].real(sa[lena - 1 - i] - '0');
for(int i = 0; i < lenb; i++) // 实部初始化
b[i].real(sb[lenb - 1 - i] - '0');
FFT(a, omg); // 系数转点值
FFT(b, omg); // 系数转点值
for(int i = 0; i < n; i++)
a[i] *= b[i]; // 点乘
FFT(a, inv); // 点值转系数 离散傅里叶变换逆变换
for(int i = 0; i < n; i++) {
res[i] += floor(a[i].real() / n + 0.5); // 离散傅里叶变换逆变换
res[i + 1] += res[i] / 10; // 进位
res[i] %= 10;
}
int len = lena + lenb - 1;
while(res[len] <= 0 && len > 0) len--;
for(int i = len; i >= 0; i--)
putchar('0' + res[i]); // 打印结果
printf("\n");
}
return 0;
}





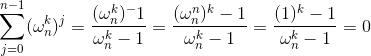

![\left \[ V_n^{-1}V_n\right \]_{jj^{'}}=\sum_{k=0}^{n-1}(\omega_n^{-kj}/n)(\omega_n^{kj^{'}})=\sum_{k=0}^{n-1}\omega_n^{k(j^{'}-j)}/n](http://img.e-com-net.com/image/info8/78e85e6f0b004159b6e6d7ecb5147e0b.gif)

