poj 1742 Coins 【多重背包+二进制拆分优化】
Coins
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3969 Accepted Submission(s): 1578
Problem Description
Whuacmers use coins.They have coins of value A1,A2,A3...An Silverland dollar. One day Hibix opened purse and found there were some coins. He decided to buy a very nice watch in a nearby shop. He wanted to pay the exact price(without change) and he known the price would not more than m.But he didn't know the exact price of the watch.
You are to write a program which reads n,m,A1,A2,A3...An and C1,C2,C3...Cn corresponding to the number of Tony's coins of value A1,A2,A3...An then calculate how many prices(form 1 to m) Tony can pay use these coins.
Input
The input contains several test cases. The first line of each test case contains two integers n(1 ≤ n ≤ 100),m(m ≤ 100000).The second line contains 2n integers, denoting A1,A2,A3...An,C1,C2,C3...Cn (1 ≤ Ai ≤ 100000,1 ≤ Ci ≤ 1000). The last test case is followed by two zeros.
Output
For each test case output the answer on a single line.
Sample Input
3 10 1 2 4 2 1 1 2 5 1 4 2 1 0 0
Sample Output
8 4
题意:给面值不同,有固定个数的硬币,能有多少种不同的不同总面值的组合方式;
思路:把多重背包问题用二进制拆分成 01 背包求解,再加上一点剪枝;
先解释一下多重背包如何优化,这里有一个数学的结论: 1到n以内的数字,能够通过 n 内的进制数组合得到,比如 9以内的二进制数有 1 2 4 8,可以自己在草稿纸上试一下, 3能通过 1 + 2 得到,5能通过1 + 4 得到,6能通过 2 + 4得到,所以,我们可以利用二进制数的拆分求出所有 n 以内的数;下面是拆分的过程:
9 - 1 = 8; 8 - 2 = 6; 6 - 4 = 2 ; 2 - 8 < 0; 那么要求的 9 以内的二进制数就是 1,2, 4,2,这几个二进制是能够组成 9以内包括 9 的所有整数,然后通过 w[ i ] 乘以这些二进制数,把他们当作一件物品来做01背包的处理,当然,如果没有用二进制拆分的话,可以直接把9拆分成 1,2,3,4,5,6,7,8,9 然后乘以w[ i ] 当作一件物品来做01背包处理,这种依次拆分的时间复杂度和不拆直接用多重背包处理是一样的,但是,为什么9个数字,只需要1,2,4,2这四个二进制数就够了呢?(这个问题暂时还没办法解决,能力有限,目前只要知道,只要拆分的二进制数字能够组成 n 以内的所有数的情况下,转化为单个物品做01背包的处理就行了),下面是代码:
#include
#include
#include
using namespace std;
#define Maxn 100010
#define INF 0x3f3f3f3f
int dp[Maxn],v[105],num[105],tmp_v[Maxn],book[Maxn];
int main(void)
{
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int kind,max_p;
while (scanf("%d%d",&kind,&max_p) != EOF) {
if(!kind && !max_p) break;
for (int i = 1; i <= kind; ++i) scanf("%d",&v[i]);
for (int i = 1; i <= kind; ++i) scanf("%d",&num[i]);
memset(dp,0,sizeof(dp));
int cnt = 1; // 用单独的数组存取拆分后的所有面值
for (int i = 1; i <= kind; ++i) {
for (int j = 1; j <= num[i]; j <<= 1) {
tmp_v[cnt] = j*v[i];
num[i]-=j;
cnt++;
}
if(num[i] > 0) tmp_v[cnt++] = num[i]*v[i];
}
//用上面拆分后的数组做01背包的处理
// 这里并没有用01背包去求最大值,而是把能够满足条件的状态dp 赋值为1,下标就是能够组合得到的总面值,
//否则为 0 ,不存在这样的面值
memset(book,0,sizeof(book));
int max_ = 1;
int ans = 0;
for (int i = 1; i < cnt; ++i) {
max_+=tmp_v[i];
max_ = min(max_p,max_);
for (int j = max_; j >= tmp_v[i]; --j) { //j的循环做了一些剪枝,因为遍历是从右往左的,在纸上模拟一下
if(dp[j]) continue; //就会明白,当前j遍历的最大值就是把以前用过的面值的累加,最小值就是
if(j == tmp_v[i]) dp[j] = 1; //当前物体的面值;
else if(j-tmp_v[i] > 0 && dp[j-tmp_v[i]]) dp[j] = 1;
if(!book[j] && dp[j]) { ans++; book[j] = 1; }
}
}
printf("%d\n",ans);
}
return 0;
}
N天后,对上面的代码进行改进,同样的一道题,要不是遇到poj,我可能以为上面的代码就很完美了,事实上,上面的代码如果交的poj的coins的话,会时间超限,而上面的代码只能在HDU的题库上AC,不得不说,这题的数据测试上,poj要强HDU很多,下面看看两个能在poj AC的代码,第一种的用时是 2800ms左右,这里的方法其实和上面的是一样的,只是在一些个别数据上面加上了完全背包来优化了时间;方法:针对一些硬币的数量,我们把他们统一做二进制拆分然后做01背包处理,假设一种硬币的数量为 10^5,那么二进制拆分得到的单个物品的数量就是 log 2(10^5),不做常数优化的01背包的情况下,一个数量为10^5的硬币时间复杂度大概就是 15*V (V是硬币组合的最大值),假设V是题目的上限 10^5,那么单个硬币的时间复杂度就是1.5*10^6,算是比较大的了,一般时间复杂度为 10^8 为比较适合的;对于这类数量巨大的数据我们如何处理? 其实仔细想想,但凡硬币的数量*硬币的价值的总和大于规定的 V 的时候,我们是不是可以直接把他当做完全背包处理,如果用完全背包的话,一个物品不用拆分就能完成这个硬币的dp操作,时间复杂度为一个V,单个数据就能快上15倍这个样子,完全背包的特点就是物品的数量可以无限取,但事实上,物品的数量*物品的价值大于规定的V的值得时候,我们是直接不考虑的;所以和上面的代码不同的就是,把硬币的数量分成两类,一类就是数量*面值大于 V的,把他当做完全背包处理,小于或者等于的话,就继续做上面代码的二进制拆分的01背包处理;下面给出代码:
#include
using namespace std;
#define Maxn 100010
int dp[Maxn],N,V,price[105],num[105];
void com_beg(int x) { // 完全背包
for (int j = price[x]; j <= V; ++j) { // 这里 j=price[x] ,是一点剪枝,建议自己独立思考一下,
// 为什么这样剪枝
if(!dp[j] && j >= price[x] && dp[j-price[x]]) dp[j] = 1;
}
}
void zero_one (int x) { // 01背包
for (int j = V; j > 0; --j) {
if(j < x) break;
if(!dp[j] && dp[j-x]) dp[j] = 1;
}
}
int main(void)
{
while (scanf("%d%d",&N,&V) != EOF) {
if(!N && !V) break;
for (int i = 0; i < N; ++i) scanf("%d",&price[i]);
for (int i = 0; i < N; ++i) scanf("%d",&num[i]);
for (int i = 1; i <= V; ++i) dp[i] = 0; // 这里初始化是可以用memeset的,但数组开的大
dp[0] = 1; // 这样也许会快一丢丢把。。
// 这里dp[0] 其实是一个确切的值,想想,背包数量为0的时候,不放不就满足条件了吗
for (int i = 0; i < N; ++i) {
if(num[i]*price[i] >= V) {
com_beg(i);
}
else {
for (int j = 1; j <= num[i]; j <<= 1) {
if(j*price[i] <= V) zero_one (j*price[i]);
num[i]-=j;
}
if(num[i] > 0 && num[i]*price[i] <= V) zero_one(num[i]*price[i]);
}
}
int ans = 0;
for (int i = 1; i <= V; ++i) if(dp[i]) ans++;
printf("%d\n",ans);
}
return 0;
}
上面就是其中的一种写法,但时间还是花费有点多,第二种方法有一个(好像很牛B的名字)多重背包可行性的名字;下面我解释一下这种方法是怎样的一个原理(是我自己理解的,也许不对,可以看看参考一下);
多重背包与完全背包和01背包最大的不同就是有限定的数量,也就是说,每一种物品限定的数量是不定的,我们回想一下最基本的多重背包是如何写的: 在01背包的基础上,多加一个循环k,k的作用就是一个限制的作用,当k 大于当前物品的数量的时候就退出,然后下一个又继续;如果我们能用别的方法代替这个k去限定物品的数量,也许就可以把这个k的循环去掉了;多重背包可行性的问题其实是一个系列的问题,都是问你一个物品能有多少种组合,而不是问你最大重量或者最小重量是多少,对于01背包和完全背包的问题上,我们用dp来表示当前的状态,并且把当前的子问题的答案存储到dp数组里头,比如,我们要求最大值,那么就把当前状态的子问题的最大值放进dp里面,那这道coins的子问题只是问我们能否组合得到,所以,可以用0和1来表示是或者否,而多重背包可行性的问题就是利用了这一点,把硬币的数量值放在dp里头,把dp的数据用一个特别的值隔开,一边表示能组合一边表示不能,而且这个数据同时还能够存储硬币的数量,来限定这个硬币的使用;下面有几张图:
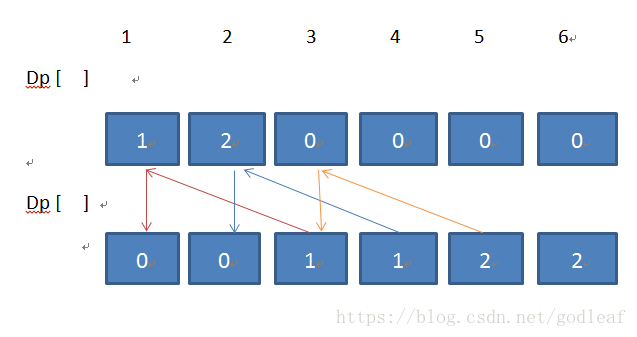
假设硬币有 两种 kind 1 和 kind 2;kind 1 的价值为1,另一个为2,数量分别为 2 和 3,V的值是6,dp【j】的j值表示的意思和上面的一样,就是罐子里面硬币的总值;
kind 1 的情况,kind 1 是第一个放入的,所以毫无疑问,能组合的总值就是kind 1 的倍数,我们一维 dp 初始化为 0 ,表示的是硬币还一次没用,当 j的 1的时候,罐子内是可以放一枚 kind 1 硬币的,然后在dp + 1,表示用了一枚了,并且用另外一个数值来存能够满足条件的组合,就是book[ 1 ] = 1; 然后 j = 2 的时候,dp【2】 == 0 && book【2】 == 0 ,说明硬币总值为 2 的罐子还没出现过(这里要注意,我们每次一个硬币只放一个),然后我们找 dp【j - price[ 1 ]】也就是 dp [ 2 - 1 ] ,发现是存在这种总值的罐子,那么我们直接在这个罐子里面投一枚 kind 1 ,就能得到 j = 2,硬币总值为 2 的罐子了,然后dp 【2】 = dp【1】+ 1;为什么 + 1?这里 + 1的意思是完成 j = 2 的时候用了已经有一枚kind 1 的总值为 1 的罐子:
既然dp【2】 已经到kind 1 数量的上限了,是不是就意味着j = 2 后面就不用遍历了呢?并不是,下面看看 kind 2 的情况就明白了:
我们先看 j = 2 的时候,j = 2的时候,显然上一次就已经用 book 记录了 book【2】 == 1;也就是说,即使不加kind 2的硬币,也能组合得到 j == 2 的罐子,所以不用放一枚kind 2 硬币,然后我们在看 j = 3 的时候,显然 book【3】 == 0,就去看dp【j - price【2】】的值,也就是 dp【3 - 2】 = dp 【1】,显然 book【1】 == 1 && dp【1】 == 0,如果当前dp【1】 == 0,说明在不用kind 2硬币的情况下存在 j == 1的罐子的组合,那么我们在 j = 1 这个罐子里头放一个 kind 2 的硬币,那就能够有j = 3 的罐子了,这里我们只用了一枚 kind 2的硬币,因为组合得到的 j = 1的罐子没用kind 2的硬币(判断dp【1】就能知道),j = 4也是一样的道理,j = 5的时候,发现book【5】== 0;那么我们就找 book【3】,book【3】= 1,注意,上图中第一行虽然dp【3】 == 0,但是在第二行的dp【3】是不为0的,说明存在j = 3的罐子,这时候发现dp【3】 = 1,说明组合得到 j = 3的时候用了一枚,那么组合得到dp【5】的时候就应该dp【5】 = dp【3】 + 1;这时候dp【5】 = 2;说明组合dp【5】用了2了两枚kind 2的硬币,以此类推,如果dp【j】大于当前硬币的数量的时候,就能直接判断不可行了;下面给出代码:
#include
#include
using namespace std;
#define Maxn 100010
int dp[Maxn],N,V,price[105],num[105],book[Maxn];
int main(void)
{
while (scanf("%d%d",&N,&V) != EOF) {
if(!N && !V) break;
for (int i = 1; i <= N; ++i) scanf("%d",&price[i]);
for (int i = 1; i <= N; ++i) scanf("%d",&num[i]);
for (int i = 0; i <= V; ++i) dp[i] = 0;
memset(book,0,sizeof(book));
book[0] = 1; // 0这种组合是无论如何都存在的
for (int i = 1; i <= N; ++i) {
for (int k = 1; k <= V; ++k) dp[k] = 0;
for (int j = price[i]; j <= V; ++j) {
if(!book[j] && book[j - price[i]] && dp[j-price[i]] < num[i]) {
dp[j] = dp[j-price[i]] + 1;
book[j] = 1;
}
}
}
int ans = 0;
for (int i = 1; i <= V; ++i) if(book[i]) ans++;
printf("%d\n",ans);
}
return 0;
}