【CQOI2017】老C的方块

传送门：NKOJ4042
这是一道网络流题。我在这道题上耗了很久=-=，感谢@OBlack帮我修改代码。
这道题的思维上的难度并不大。
以下是我的想法：
首先要确定一个大的方向，题目中要求移除一些方块使得剩余方块无法构成“讨厌的形状”，很容易就想到了最小割。

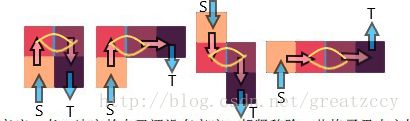
仔细观察一下，可以发现这些讨厌的形状是由两个方格+一条特殊的边+两个方格按不同方向摆放而成的。

于是可以根据观察所得将网格染成如图4种颜色：

讨厌的形状便是根据“浅橙—红—浅棕—深棕”或“深棕—红—浅棕—浅橙”的顺序构成的。

谈谈建图：

如上图，蓝色边容量为方格的权值，粉色边容量为inf，黄色边容量为相关联的两个方格中较小的权值。

建好图就可以愉快地跑SAP了。（提醒自己以后pid要赋初值，因为1^1=0而我想要找的是2号边。要更细致些啊，向OBlack学习(ง •_•)ง）
放出渣代码吓人：

#include
#include
#include
#define LL long long
const int MAXN=400005;
const LL inf=1e10;
using namespace std;
LL To[MAXN<<1],Next[MAXN<<1],Last[MAXN],pid=1;
LL C,R,n,S,T;
LL W[MAXN];
struct node {
    LL X,Y,w;
} pane[MAXN];
mapID;
void storepath(LL u,LL v,LL w)
{
    To[++pid]=v,Next[pid]=Last[u],Last[u]=pid,W[pid]=w;
    To[++pid]=u,Next[pid]=Last[v],Last[v]=pid,W[pid]=0;
}
LL getid(LL x,LL y)
{
    return x+(y-1)*C;
}
LL Judge(LL x,LL y)
{
    LL t;
    if(y&1) {
        t=x%4;
        if(t)return t;
        return 4;
    }
    t=(x+2)%4;
    if(t)return t+4;
    return 8;
}
void U_D_in(LL i,LL x,LL y)
{
    LL id=getid(x,y),tid;
    tid=id+C;
    if(ID.count(tid))storepath(ID[tid],i,inf);
    tid=id-C;
    if(ID.count(tid))storepath(ID[tid],i,inf);
}
void U_D_out(LL i,LL x,LL y)
{
    LL id=getid(x,y),tid;
    tid=id+C;
    if(ID.count(tid))storepath(i,ID[tid],inf);
    tid=id-C;
    if(ID.count(tid))storepath(i,ID[tid],inf);
}
void FL_in(LL i,LL x,LL y)
{
    LL id=getid(x,y),tid;
    tid=id-1;
    if(x-1&&ID.count(tid)) {
        storepath(ID[tid],i,inf);
    }
}
void TL_out(LL i,LL x,LL y)
{
    LL id=getid(x,y),tid;
    tid=id-1;
    if(x-1&&ID.count(tid)) {
        storepath(i,ID[tid],inf);
    }
}
void TR_out(LL i,LL x,LL y)
{
    LL id=getid(x,y),tid;
    tid=id+1;
    if(x+1<=C&&ID.count(tid)) {
        storepath(i,ID[tid],inf);
    }
}
void FR_in(LL i,LL x,LL y)
{
    LL id=getid(x,y),tid;
    tid=id+1;
    if(x+1<=C&&ID.count(tid)) {
        storepath(ID[tid],i,inf);
    }
}
void Build()
{
    LL x,y,id,tid,t,co;
    for(int i=1; i<=n; i++) {
        x=pane[i].X,y=pane[i].Y,id=getid(x,y);
        co=Judge(x,y);
        if(co==1||co==5) {
            tid=id+1;
            if(x+1<=C&&ID.count(tid)) {
                t=min(pane[i].w,pane[ID[tid]].w);
                storepath(i,ID[tid],t),W[pid]=t;
                if(co==1)U_D_in(i,x,y),FL_in(i,x,y);
                else U_D_out(i,x,y),TL_out(i,x,y);
            }
        } else if(co==2||co==6) {
            tid=id-1;
            if(ID.count(tid)) {
                if(co==2)U_D_out(i,x,y),TR_out(i,x,y);
                else U_D_in(i,x,y),FR_in(i,x,y);
            }
        } else if(co==3||co==8) {
            storepath(i,T,pane[i].w);
        } else {
            storepath(S,i,pane[i].w);
        }
    }
}
LL dis[MAXN],cnt[MAXN];
LL SAP(LL u,LL flow)
{
    if(u==T)return flow;
    LL out=0,tmp;
    for(int i=Last[u]; i>1; i=Next[i]) {
        if(!W[i]||dis[u]!=dis[To[i]]+1)continue;
        out+=tmp=SAP(To[i],min(flow-out,W[i]));
        W[i]-=tmp,W[i^1]+=tmp;
        if(flow==out||dis[S]>=T)return out;
    }
    if(!--cnt[dis[u]])dis[S]=T;
    cnt[++dis[u]]++;
    return out;
}
int main()
{
    scanf("%lld%lld%lld",&C,&R,&n);
    for(int i=1; i<=n; i++) {
        scanf("%lld%lld%lld",&pane[i].X,&pane[i].Y,&pane[i].w);
        ID[getid(pane[i].X,pane[i].Y)]=i;
    }
    S=n+1,T=S+1;
    Build();
    LL ans=0;
    while(dis[S]printf("%lld",ans);
    return 0;
}