论文笔记- Improving Word Representations via Global Context and Multiple Word Prototypes
综述
提出了一种新的基于神经网络的语言模型,通过对局部上下文和全局上下文进行联合训练。该模型学习到的embedding能同时捕捉到单词语义信息和语法信息,并且能够实现对一词多义的区分。
目标函数
本文的目标是学习有效的单词表示,而不是根据给定的单词来预测下一个单词的概率。给定序列s和文档d,本文的目标是从其它随机选择的单词中找到位于s末尾的正确单词。替换单词后的序列为 s w s^w sw。
C s , d = ∑ w ∈ V max ( 0 , 1 − g ( s , d ) + g ( s w , d ) ) C_{s, d}=\sum_{w \in V} \max \left(0,1-g(s, d)+g\left(s^{w}, d\right)\right) Cs,d=w∈V∑max(0,1−g(s,d)+g(sw,d))
其中 g ( s , d ) g\left(s, d\right) g(s,d)为得分函数, s s s与 s w s^w sw之间的差值被限制在 ( 0 , 1 ) (0,1) (0,1)范围内。
神经网络架构
本文同时从局部上下文和全局上下文的角度来考虑上下文信息。局部和全局上下文计算得到的分数 s o c r e l socre_{l} socrel和 s c o r e g score_{g} scoreg相加得到总的分数 g ( s , d ) g\left(s, d\right) g(s,d)。
局部上下文
对于序列s,将s中的单词的embedding拼接成一个向量 X = { x 1 , x 1 , . . . , x m } X=\{x_{1}, x_{1}, ..., x_{m}\} X={x1,x1,...,xm},经过一个两层的全连接神经网络:
a 1 ( l ) = f ( W 1 ( l ) [ x 1 , x 1 , . . . , x m ] + b 1 ( l ) ) a_{1}^{(l)}=f\left(W_{1}^{(l)}\left[x_{1}, x_{1}, ..., x_{m}\right]+b_{1}^{(l)}\right) a1(l)=f(W1(l)[x1,x1,...,xm]+b1(l))
s c o r e l = W 2 ( l ) a 1 ( l ) + b 2 ( l ) score _{l}=W_{2}^{(l)} a_{1}^{(l)}+b_{2}^{(l)} scorel=W2(l)a1(l)+b2(l)
全局上下文
假设当前文档中包含有k个单词,那么对它们计算加权平均可以得到向量c,用来表示全局上下文信息
:
c = ∑ i = 1 k w ( t i ) t i ∑ i = 1 k w ( t i ) c=\frac{\sum_{i=1}^{k} w\left(t_{i}\right) t_{i}}{\sum_{i=1}^{k} w\left(t_{i}\right)} c=∑i=1kw(ti)∑i=1kw(ti)ti
其中 w ( t i ) w(t_{i}) w(ti)为单词 t i ti ti的权重函数,在这里采用idf权重来计算。
然后,将 c c c和 x m x_{m} xm拼接成一个向量,经过一个两层的全连接神经网络:
a 1 ( g ) = f ( W 1 ( g ) [ c ; x m ] + b 1 ( g ) ) a_{1}^{(g)}=f\left(W_{1}^{(g)}\left[c ; x_{m}\right]+b_{1}^{(g)}\right) a1(g)=f(W1(g)[c;xm]+b1(g))
s c o r e g = W 2 ( g ) a 1 ( g ) + b 2 ( g ) score _{g}=W_{2}^{(g)} a_{1}^{(g)}+b_{2}^{(g)} scoreg=W2(g)a1(g)+b2(g)
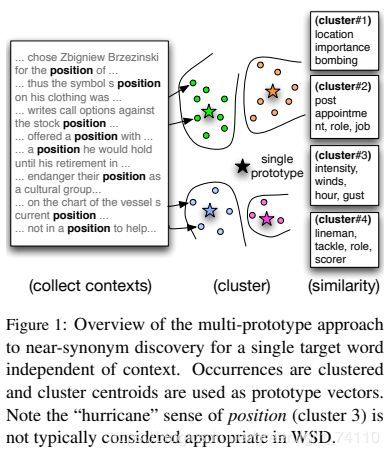
一词多义(Multi-Prototype Neural Language Model)
每个词在不同的上下文中有着不同的含义,本文希望根据上下文信息给每个词加一个相应的标签,使得每个词可以对应不止一个embedding表示。
- 对某个单词w,首先获取其所有的上下文窗口序列。
- 对每个上下文窗口序列,对序列内的所有单词embedding取加权平均,作为该序列的embedding表示,方法参考全局上下文中的做法。
- 对这序列的embedding进行球形(spherical)k-means聚类,得到每个序列的类比编号。ps:简单来说,球形与普通k-means的区别在于,球形的相似度度量是余弦距离,而不是标准欧氏距离。
- 按照聚类结果,给每个单词的后面加上属于它的类别编号,例如bank_1,bank_2。
在multi-prototype模型下,两个词的相似度计算如下:
Avg Sim C ( w , w ′ ) = 1 K 2 ∑ j = 1 K ∑ k = 1 K d c , w , k d c ′ , w ′ , j d ( π k ( w ) , π j ( w ′ ) ) \operatorname{Avg} \operatorname{Sim} \mathrm{C}\left(w, w^{\prime}\right) = \frac{1}{K^{2}} \sum_{j=1}^{K} \sum_{k=1}^{K} d_{c, w, k} d_{c^{\prime}, w^{\prime}, j} d\left(\pi_{k}(w), \pi_{j}\left(w^{\prime}\right)\right) AvgSimC(w,w′)=K21j=1∑Kk=1∑Kdc,w,kdc′,w′,jd(πk(w),πj(w′))
其中 d c , w , k = def d ( v ( c ) , π k ( w ) ) d_{c, w, k} \stackrel{\text { def }}{=} d\left(v(c), \pi_{k}(w)\right) dc,w,k= def d(v(c),πk(w))可以看作是 w w w对应的上下文 c c c属于聚类 k k k的似然概率, π k ( w ) \pi_{k}(w) πk(w)表示聚类 k k k的中心点, d ( π k ( w ) , π j ( w ′ ) ) d\left(\pi_{k}(w), \pi_{j}\left(w^{\prime}\right)\right) d(πk(w),πj(w′))表示两个聚类中心的相似度。
如果没有上下文,那上式就可以简化为:
AvgSim ( w , w ′ ) = def 1 K 2 ∑ j = 1 K ∑ k = 1 K d ( π k ( w ) , π j ( w ′ ) ) \operatorname{AvgSim}\left(w, w^{\prime}\right) \stackrel{\text { def }}{=} \frac{1}{K^{2}} \sum_{j=1}^{K} \sum_{k=1}^{K} d\left(\pi_{k}(w), \pi_{j}\left(w^{\prime}\right)\right) AvgSim(w,w′)= def K21j=1∑Kk=1∑Kd(πk(w),πj(w′))