（9）图像编码与压缩（Image Coding and Compression）

Table of Contents

1.图像压缩简介

2.图像压缩用途

3. 源编码与信道编码

4. 有损压缩与无损压缩

2. 图像压缩的必要性

常见的压缩标准

图像压缩的基本流程

JPEG的压缩方法

3. 量化

4. 常用编码方法

1.KLT

2. DCT

5. Huffman编码与信息熵

为什么要进行编码？

概率高的符号用短码，概率低的符号用长码

Huffman编码生成方式

理论最小平均码长(信息熵)

三叉Huffman编码方法

6. OpenCV+C++语言实现图像压缩

---

PART I 图像编码

1.图像压缩简介

• 图像编码是指在空间域下对图像像素值进行编码，其典型的用途是：

1. 图像压缩
2. 图像加密
3. 图像水印等

• 图像编码压缩的主要目的是用尽可能少的bits去表示一副图像，于此同时，图像的质量和信息得以保留。
• 衡量压缩质量的主要标准：MSE（Mean Square Error）均方误差、PSNR（Peak Signal to Noise Ratio）峰值信噪比、SSIM（Structural similarity index）等。

2.图像压缩用途

1. 减少信道传输时所需的带宽；
2. 减少存储时所需的磁盘空间。

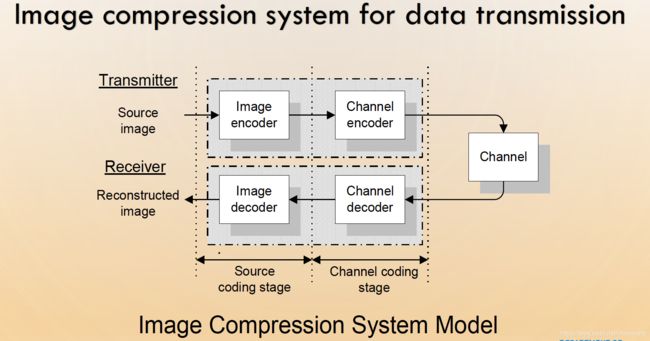
3. 源编码与信道编码

4. 有损压缩与无损压缩

---

2. 图像压缩的必要性

　　某天陈老师要录动作大片，经过长期艰苦奋斗，他制成了这样一段视频：画面大小1000×1000pixel，24位真彩色，每秒30帧，时长2小时。
　　如果不进行任何压缩，存储这段视频需要1000*1000*24*30*60*120=5.184 ×1012 bit ≈ 648GB的空间。(2014年4月5日,500GB硬盘最低价格是299元~)
　　用4M宽带下载这部大片，最少需要360小时 = 15天。
　　可见，要保障人民群众的切身利益，压缩技术非常有必要。

压缩的可能性

　　就单幅图像而言，压缩的可能性是显而易见的。
　　如上面三幅小图，图a每个形状里面都填充着相同的颜色，图b每一行的颜色是相同的，更过分的图c整幅图只填充了一种颜色。
　　压缩前：第1个点灰色，第2个点灰色，第3个点灰色，第4个点灰色，第5个点灰色，第6个点灰色......第89个点灰色，第90个点黑色......
　　最简单的压缩后：第1到89个点灰色，第90个点黑色。

常见的压缩标准

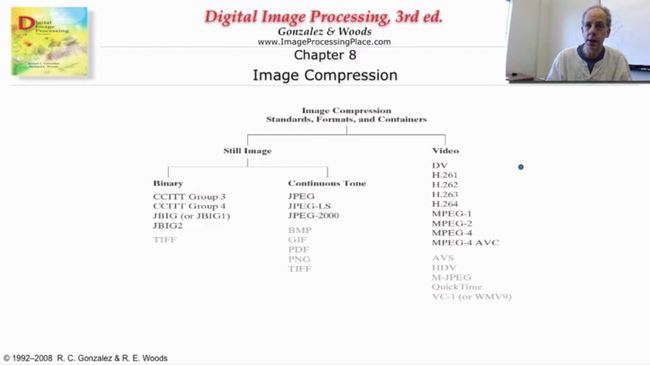
　　JPEG是广泛使用的照片存储格式，它适应人的视觉，用更多的数据来存储人眼敏感的图像低频部分，用很少的数据存储人眼不关心的高频部分。维基百科有很详尽的讲解http://zh.wikipedia.org/wiki/JPEG
　　JPEG 2000是基于小波变换的图像压缩标准，可以获得比JPEG更大的压缩比，通常它被认为是未来取代JPEG的标准。http://zh.wikipedia.org/wiki/JPEG_2000

图像压缩的基本流程

图像压缩基本按照以下流程进行：
原图像 -> 映射 -> 量化 -> 符号编码 -> 存储/传输 -> 符号解码 -> 反映射 -> 图像
映射(Mapper)：对原图像进行变换，使之更容易被压缩。(比如傅里叶变换)
量化(Quantizer)：量化是压缩的主要图像，主要也是它引入误差的。比如有一个以2为单位的量化器，看到原图像值是17，将它除2向下取整，量化得到8；图像还原的时候，用8×2=16得到还原值，与真实值相差了1。
符号编码(Symbol encoder)：图像已经变换量化完了，该为存储和传输作准备了。符号编码可以进一步地压缩文件大小：将重复出现次数多的数据，用简短的符号进行编码；出现次数少的数据，用较长的符号进行编码；后面的哈夫曼(Huffman)编码会详细讲到~

JPEG的压缩方法

　　鉴于图像压缩的每个步骤都能有不同的方法，所以有必要制定统一的标准，使得图像在每台电脑每部手机中都能正常使用。
　　JPEG是其中一个标准，它的压缩套路如下：
　　原图像 -> 分解成一个个小图像 -> 变换 -> 量化 -> 符号编码 -> 压缩后的图像
　　分解图像：JPEG会将一幅大图像分解成8×8的小图像。至于为什么是8×8呢，嗯，欢迎各位同学剧透；
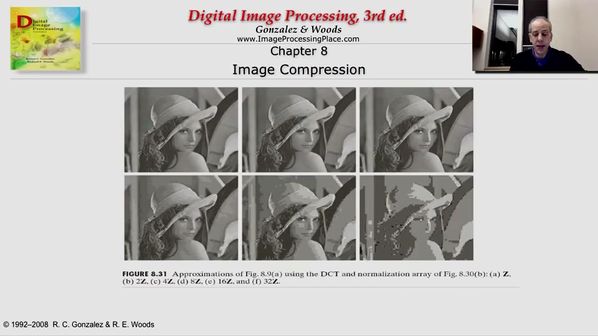
　　变换：JPEG使用DCT变换(离散余弦变换)，类似傅里叶变换，不过它是取实部。(不由感慨，学好“信号与系统”也是很有必要的...)
　　量化：JPEG通过各种除法来进行量化，不过对于不同重要程度的信息，它所除的数的大小会有所不同；
　　符号编码：JPEG使用常见的哈夫曼(Huffman)编码。
　　图像还原，就是反过来进行这些步骤。
　　JPEG的实现方法比较简单，也因为简单高效，所以JPEG的应用范围相当广泛。

---

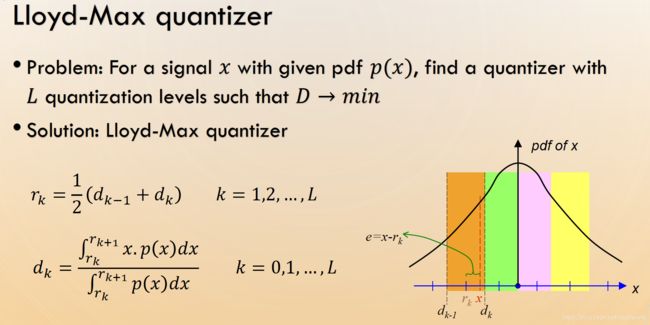
3. 量化

数字图像与模拟图像的重要区别，在与它是数字的。(还能有更废的话吗...)数字，意味着它的离散的：图像空间上的像素点是离散的，像素点的灰度值(颜色值)也是离散的。相反，模拟图像(比如胶卷)出来的图像空间上和数值上都是连续的。

下图是JPEG的压缩编码流程，本节介绍的，是其中的“量化”(Quantizer)部分。

JPEG的压缩方法，可以所是非常聪明。
人眼看图像，不会太注重细节。左边一个像素与右边一个像素灰度值相差10或是11，基本不会影响理解。
简单地说，JPEG用最多的空间，来存储对人理解最重要的信息，而一些微乎其微的小细节，基本不会储存。

打个比方，JPEG是这样描述一个图像的：
1. 这是一个人；
2. 是一个女人；
3. 1.7米高，三围Beep——
4. 肤色棕黑；
5. 眼睛大大，鼻子高高；
6. 牙齿奶黄色，身上有不显眼的体毛；
7. 体毛长度介于1.2cm-1.3cm；
8. 体毛的弧度可以用这个函数表示(省略)；
9. 毛上面有这么些粗糙的细节；
10. 毛上面粗糙的细节的纹路是这样字的。
11. (更加细微和揪心的...)
上面是从对人理解的重要性高到低排序的，只要看到1-9，人就能很好地理解这个图像了。(不是我喜欢的类型~！) 那些微观的细节，对人理解没有太大帮助，而存储它占据的空间是跟存储前面宏观内容是一样的。
所以，

JPEG是用更多空间存储“大”的东西，而用更少空间存储“微小的细节”，这样图像大小就能大大地被压缩，而不影响人的理解。

Lloyd—Max quantizer

 

---

4. 常用编码方法

1.KLT

KLT的不足：

2. DCT

 

---

5. Huffman编码与信息熵

JPEG用哈夫曼编码(Huffman Encoder)作为其符号编码。哈弗曼编码是压缩算法中的经典，它理论上可以将数据编成平均长度最小的无前缀码(Prefix-Free Code)。

为什么要进行编码？

关于Lena：莱娜图（Lenna）是指刊于1972年11月号《花花公子》（Playboy）杂志上的一张裸体插图照片的一部分，是一张大小为512x512像素的标准测试图。该图在数位影像处里学习与研究中颇为知名，常被用作数位影像处里各种实验（例如资料压缩和降噪）及科学出版物的例图。(几乎每一本图像处理相关的书都会出现这张图片~)
Lena的直方图(Histogram)：从Lena的直方图中可以看出，图片中每个灰度值出现的概率是不相同的。这里，中间灰度值部分出现的概率比较高，两边灰度值出现概率非常低。所以，如果每个灰度值都进行同样长度的编码，似乎就太浪费了。

 

概率高的符号用短码，概率低的符号用长码

正是因为每个灰度值出现的概率不一样，我们用更短的编码来表示经常出现的灰度值，用更长的编码来表示几乎不出现的灰度值，平均下来编码长度就会比等长编码短，从而节省了空间。

Huffman编码生成方式

1. 将要编码的符号按出现概率高到低排列；
2. 将出现概率最低的两个符号进行组合，两者概率加起来得到组合概率；
3. 将得到的组合概率与其他符号的概率再进行排序；
4. 重复(2)，直到出现组合概率为1。

首先，按照各符号出现概率大小进行排列；

找到概率最小的两个符号，进行组合。这里是a3和a5最小，两者组合起来概率为0.1；

将组合好的两个符号看作一个新的符号，与其他符号再进行一次排列，找到出现概率最小的两个；

将两个出现概率小的符号再进行一次组合，有得到一个组合概率；

如此进行下去，知道组合到概率为1；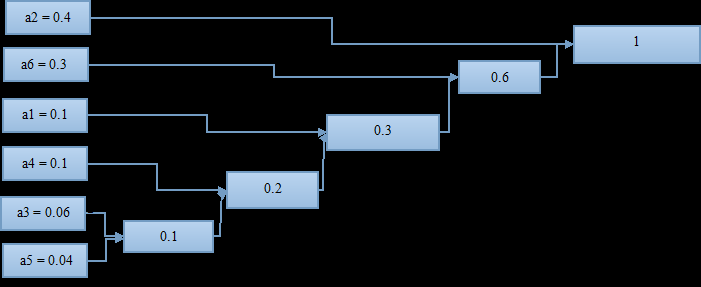

至此，这棵哈夫曼“树”算是画完了，可以进行编码了；
从概率为1(最右)开始，上面分叉编号1，下面分叉编号0(反过来也可以)，编号到最左边。
从右到左读数：

a2 = 1;
a6 = 01;
a1 = 001;
a4 = 0001;
a3 = 00001;
a5 = 00000;

哈夫曼编码的一大好处是，它是Prefix-Free的，也就是每个符号之间不加分隔符，解码器也能识别；
对上面6个符号，如果采用统一长度编码，一个符号需要3bit；
用哈夫曼进行编码，

平均码长 = 1*0.4 + 2*0.3 + 3*0.1 + 4*0.1 + 5*0.06 + 5*0.04 = 2.2bit;
压缩比 = 2.2/3=0.7333333333;

如果概率分布更集中，压缩效果更明显。

 

理论最小平均码长(信息熵)

我还依稀记得，香农老人家语重心长地教诲我：哈夫曼编码的最小平均码长，是熵(信息论)。
不过实践经验告诉我，一般哈夫曼编码出来的平均码长，会比这个理论值大那么一丢丢。

三叉Huffman编码方法

经历完上学期的“信息论”考试，我才知道，地球上还存在N叉哈夫曼编码。
一般二叉都会使用二叉哈夫曼编码，也就是用0、1作为分叉。
但考试非要考三叉哈夫曼编码，也就是用0、1、2来进行编码。
方法很简单：方法与二叉Huffman编码一致，如果待编码的符号数不是3的倍数，就自行补上几个“概率为0”的符号，使符号的总个数为3的倍数。

JPEG分块对图像进行处理

　　JPEG压缩图像的第一步，是将图像分解成一个个8×8的小图像，之后再分别对这些小图像进行变换量化编码。

为什么JPEG要使用8×8的分块？

1. 分块小，比如2×2，图像还原质量差；
2. 分块大，比如将整幅图作为一块，消耗计算资源多；
平衡质量和资源，JPEG默认使用8×8的分块。当然，我觉得一定是有更深层原因的....

用YCrCb表示颜色

　　JPEG是“色盲”的，它不能直接作用于彩色图像。要处理彩色图像，显而易见的解决办法是分别对RGB三个通道进行处理，后果是，图像中三种颜色的联系被活活的拆散了。因此，JPEG采用YCrCb来表示颜色。
　　想当年，黑白电视占主流，彩色电视刚面世。为了使黑白电视也能看到彩色电视信号装载的节目，聪明的人类想到了一种办法：用Y通道表示图像的亮度，CrCb表示色差，这样黑白电视只接收Y通道的信号，就能看到黑白图像；彩色电视则通过YCbCr，来获得彩色图像。也因为人对图像的亮度比较敏感，可以用更多数据来传输Y通道，用更少数据来传送CbCr通道，从而提升图像压缩率。

---

6. OpenCV+C++语言实现图像压缩

见另一篇博客