主席树(POJ-2104、HDU-2665)
【算法分析】
主席树名称来源于其发明人黄嘉泰的姓名的首字母缩写HJT与我们某位主席姓名的首字母缩写一样。
主席树的经典应用在于求某个区间内的第K小/大数的值。比如区间第K大问题,就是给定一个数列a,询问给定区间[L,R]的第K大值。如对数列a=[4,1,3,2,5],针对询问L=2,R=5,K=2,其答案为2。
主席树是一种可持久化数据结构,即可持久化权值线段树。
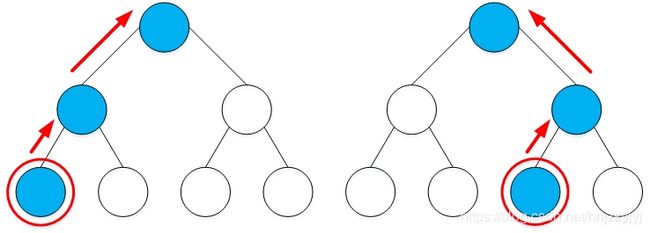
为了实现可持久化,就要保存线段树的历史版本。最自然的想法是每进行一次修改,就新建一棵线段树,显然这样的空间复杂度是无法接受的。通过观察不难发现,每次单点修改,发生变化的只有从叶结点到根结点这一条路径上的结点。换句话说,只有log₂n个结点发生了变化,而其他的结点都可以重用,没有必要新建。
- 权值线段树一般开32倍空间,而普通线段树一般开4倍空间。若构建主席树,需先了解权值线段树的构建过程。
- 权值线段树以给定序列的值域作为区间进行结点构建。权值线段树每个结点存储的是所示值域上值的个数。
有n个结点的主席树,包含n棵权值线段树。n棵权值线段树的形状是一模一样的,只是结点的权值不一样。
下面给出构建权值线段树实例的具体步骤(https://www.bilibili.com/video/av56485341/):
1.给定序列1,1,2,3,3,3,4,4,显见其值域为[1,4]。
2.以区间[1,4]作为根结点所示区间构建线段树(与构建普通线段树方法一致)。
3.从叶子结点开始,由下向上,将第2步所建线段树中各个结点的权值赋值为其所示区间对应的原始序列中相应元素的个数,就构建成了一棵权值线段树。如区间[1,1]结点,其值为给定序列中1的个数2;区间[3,3]结点,其值为给定序列中3的个数3;区间[1,4]结点,其值为给定序列中1、2、3、4的总个数8。可见,权值线段树中的结点相当于桶排序中的桶。
由上算法,依据给定序列1,1,2,3,3,3,4,4创建的权值线段树示意图如下: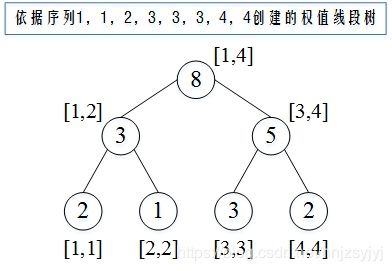
主席树是所有历史版本的权值线段树的集合。所以利用主席树,可以查询历史版本的权值线段树。 主席树构建时,若给定数据的个数大于100000,需采用离散化方法。所谓离散化,就是把无限空间中有限的个体映射到有限的空间中去,以提高算法的时空效率。通俗的说,离散化是在不改变数据相对大小的前提下,对数据进行相应的缩小。例如:25957,6405,15770,26287,26465离散化的结果为3,1,2,4,5
【程序代码】
#include
using namespace std;
const int maxn=1e5+10;
struct node {
int l,r,sum;
} t[maxn<<5];
int cnt;
int root[maxn];
int a[maxn];
vectorv;
int getid(int x) {
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void insert(int l,int r,int pre,int &now,int p) {
t[++cnt]=t[pre];
now=cnt;
t[now].sum++;
if (l==r) {
return;
}
int mid=(l+r)>>1;
if (p<=mid) {
insert(l,mid,t[pre].l,t[now].l,p);
} else {
insert(mid+1,r,t[pre].r,t[now].r,p);
}
}
int query(int l,int r,int L,int R,int k) {
if (l==r)
return l;
int mid=(l+r)>>1;
int tmp=t[t[R].l].sum-t[t[L].l].sum;
if (k<=tmp) {
return query(l,mid,t[L].l,t[R].l,k);
} else {
return query(mid+1,r,t[L].r,t[R].r,k-tmp);
}
}
int main() {
int n,m;
cin>>n>>m;
for (int i=1; i<=n; i++) {
cin>>a[i];
v.push_back(a[i]);
}
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
for (int i=1; i<=n; i++) {
insert(1,n,root[i-1],root[i],getid(a[i]));
}
while (m--) {
int l,r,k;
cin>>l>>r>>k;
cout<
【参考文献】
https://blog.csdn.net/weixin_42165981/article/details/81131661
https://blog.csdn.net/ModestCoder_/article/details/90107874
https://blog.csdn.net/woshinannan741/article/details/53012682
https://blog.csdn.net/Stupid_Turtle/article/details/80445998
https://www.bilibili.com/video/av16552942
https://blog.csdn.net/cj1064789374/article/details/85037178
https://www.cnblogs.com/zxytxdy/p/11767047.html
https://blog.csdn.net/pengwill97/article/details/80920143
https://blog.csdn.net/creatorx/article/details/75446472
https://blog.csdn.net/qq_39809664/article/details/79934516
https://blog.csdn.net/a_forever_dream/article/details/80450549