Pytorch打卡第2天：张量、计算图、线性回归、逻辑回归

一、张量的操作

拼接

• torch.cat(): 将张量按维度dim进行拼接
• torch.stack()：在新建的维度dim上进行拼接

t = torch.ones((2, 3))

t_0 = torch.cat([t, t], dim=0)
t_1 = torch.stack([t, t], dim=0)

print(t_0)
print(t_0.shape)
print(t_1)
print(t_1.shape)

切分

• torch.chunk(input, chunks, dim): 将张量按维度dim进行平均切分

t = torch.ones((2, 7))
print(t)

list_of_tensor = torch.chunk(t, dim=1, chunks=3)
print(list_of_tensor)

• torch.split(): 将张量按维度dim进行切分

t = torch.ones((2, 7))
print(t)
list_of_tensor_2 = torch.split(t, 3, dim=1)
print(list_of_tensor_2)

list_of_tensor_3 = torch.split(t, [2, 2, 3], dim=1)
print(list_of_tensor_3)

索引

• torch.index_select(): 在维度dim上，按index索引数据

t = torch.randint(0, 9, (3, 3))
print(t)

# index_select
idx=torch.tensor([0,2],dtype=torch.long)
t_index_select=torch.index_select(t,index=idx,dim=0)
print(t_index_select)

• torch.masked_select(): 按mask中的True进行索引， 返回一维张量。

t = torch.randint(0, 9, (3, 3))
print(t)

# masked_select
mask = t.ge(5)
print(mask)

t_masked_select = torch.masked_select(t, mask)
print(t_masked_select)

变换

• torch.reshape: 变换张量形状
  notice: 注意事项:当张量在内存中是连续时，新张 量与input共享数据内存

# torch.reshape
t = torch.randperm(8)
print(t)
t_reshape = torch.reshape(t, (2, 4))  # -1代表不关心
print(t_reshape)

• torch.transpose(): 交换张量的两个维度

# torch.transpose
t = torch.rand((2, 3, 4))
print(t)
t_transpose = torch.transpose(t, dim0=1, dim1=2)
print(t_transpose)

• torch.t(): 2维张量转置，对矩阵而言，等价于 torch.transpose(input, 0, 1)

• torch.squeeze(): 压缩长度为1的维度(轴)

# torch.squeeze
t=torch.rand((1,2,3,1))

t1=torch.squeeze(t)
print(t1.shape)

t2=torch.squeeze(t,dim=2)
print(t2.shape)

• torch.unsqueeze(): 依据dim扩展维度

---

二、张量的数学运算

• torch.add(): 逐元素计算 input+alpha×other

# torch.add
t0=torch.rand((3,3))
t1=torch.ones_like(t0)
print(t0)
print(t1)
t_add=torch.add(t0,10,t1)
print(t_add)

• torch.addcdiv()
• torch.addcmul()

---

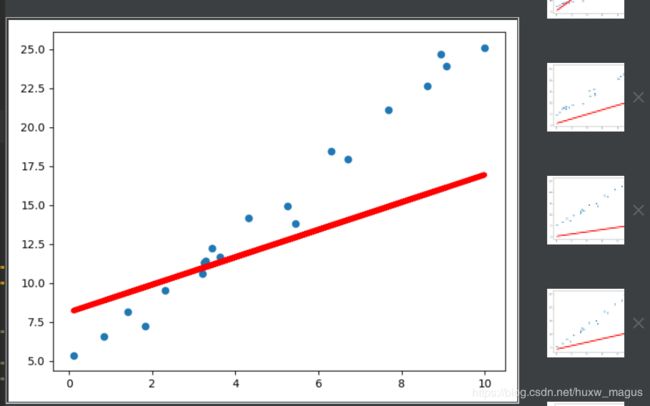
三、线性回归

import torch
import numpy as np
import matplotlib.pyplot as plt

lr = 0.1

# 创建训练数据
x = torch.rand(20, 1) * 10
# print(x)
y = 2 * x + (5 + torch.randn(20, 1))

# 构建回归参数
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)

for iteration in range(300):
    # 前向传播
    wx = torch.mul(w, x)
    y_pred = torch.add(wx, b)

    # 计算MSE loss
    loss = (0.5 * (y - y_pred) ** 2).mean()

    # 后向传播,得到梯度
    loss.backward()

    # 更新参数
    b.data.sub_(lr*b.grad)
    w.data.sub_(lr*w.grad)

    # 绘图
    if iteration%100==0:

        plt.scatter(x.data.numpy(),y.data.numpy())
        plt.plot(x.data.numpy(),y_pred.data.numpy(),'r-',lw=5)
        plt.pause(0.5)

        if loss.data.numpy()<1:
            break
            

---

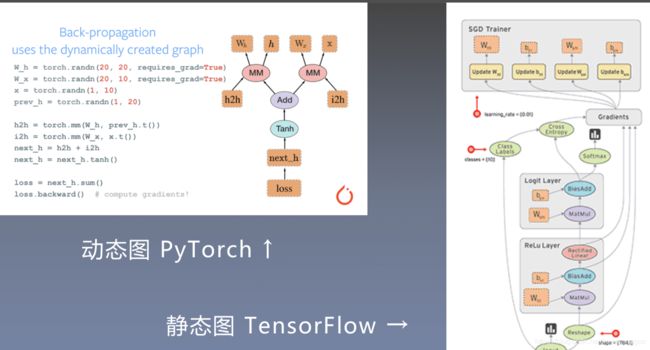
计算图

叶子结点很重要

• retain_grad(): 保留非叶子结点的梯度，防止被释放掉
• is_leaf(): 查看是否为叶子结点，返回：True / False
• grad_fn: 记录创建该张量时所用的方法 (函数)

import torch
import numpy as np
import matplotlib.pyplot as plt

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

y.backward()
print(w.grad)

# 查看叶子结点
print(a.is_leaf, b.is_leaf, w.is_leaf)

# 查看梯度
print(w.grad, x.grad, a.grad)

# 查看grad_fn
print(w.grad_fn, a.grad_fn)

返回值：

tensor([5.])
False False True
tensor([5.]) tensor([2.]) None
None <AddBackward0 object at 0x12204aed0>

---

动态图

---

Autograd

torch.autograd.backward: 自动求取梯度

• tensors: 用于求导的张量，如 loss

• retain_graph : 保存计算图

• create_graph : 创建导数计算图，用于高阶求导

• grad_tensors:多梯度权重

• 代码

import torch
import numpy as np
import matplotlib.pyplot as plt

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)
y0 = torch.mul(a, b)
y1 = torch.add(a, b)

loss = torch.cat([y0, y1], dim=0)
print(loss)

# 权重的设置
grad_tensors = torch.tensor([1., 1.])

loss.backward(gradient=grad_tensors)

print(w.grad)

• 结果

tensor([6.], grad_fn=<MulBackward0>) tensor([5.], grad_fn=<AddBackward0>)
tensor([6., 5.], grad_fn=<CatBackward>)
tensor([7.])

Process finished with exit code 0

torch.autograd.grad: 求取梯度

• outputs: 用于求导的张量，如 loss
• inputs : 需要梯度的张量
• create_graph : 创建导数计算图，用于高阶求导
• retain_graph : 保存计算图
• grad_outputs:多梯度权重

import torch
import numpy as np
import matplotlib.pyplot as plt

x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2)

# 一次求导
gard_1 = torch.autograd.grad(y, x, create_graph=True)  # res = 6
print(gard_1)

# 二次求导
grad_2 = torch.autograd.grad(gard_1[0], x)  # res = 2
print(grad_2)

autograd小贴士:

1. 梯度不自动清零，会叠加
2. 依赖于叶子结点的结点，requires_grad默认为True
3. 叶子结点不可执行in-place（原位’_’）

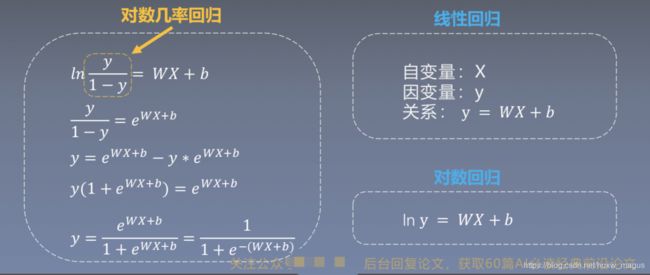
逻辑回归

机器学习的五大步：

• 数据
• 模型
• 损失函数
• 优化器
• 迭代训练

import torch
import torch.nn as nn

import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(10)

# step1: 生成数据
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)  # dim = 100x2

x0 = torch.normal(mean_value * n_data, 1) + bias  # 正态分布的随机数
y0 = torch.zeros(sample_nums)

x1 = torch.normal(-mean_value * n_data, 1) + bias
y1 = torch.ones(sample_nums)

train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)


# step2: 模型选择


class LR(nn.Module):
    def __init__(self):
        super(LR, self).__init__()
        self.features = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = self.features(x)
        x = self.sigmoid(x)
        return x


# 实例化
lr_net = LR()

# step3: loss
loss_fn = nn.BCELoss()

# step4: optimizer
lr = 0.01  # learning rate
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)

# 训练

for iteration in range(1000):
    # 向前传播
    y_pred = lr_net(train_x)

    # 计算loss
    loss = loss_fn(y_pred.squeeze(), train_y)

    # 反向传播
    loss.backward()

    # 更新参数
    optimizer.step()

    # 绘图
    if iteration % 50 == 0:
        # 以0.5进行分类
        mask = y_pred.ge(0.5).float().squeeze()
        
        # 计算正确预测的样本数
        correct = (mask == train_y).sum()
        
        # 计算准确率
        acc = correct.item() / train_y.size(0)
        print(acc)

        # ...

        if acc > 0.999:

            break