学习笔记-Matlab之多项式详解

本文内容概述：

• 1、多项式的表示
• 2、多项式的计算
  • polyval函数
• 3、多项式的根
  • 1）数值根
    • roots函数
    • poly函数
  • 2）符号根
  • 特定区间内的根
    • fzero()
• 4、多项式求微分和积分
  • 1）求微分/求导数
    • polyder函数
  • 2)求微分
    • polyint函数
• 5、多项式曲线的拟合
  • polyfit函数

正文

多项式：诸如$p_n{x}^n+p_{n-1}{x}^{n-1}+...+p_2{x}^2+p_{1}x+p_0$，包含非负整数指数的单个变量的表达式。

1、多项式的表示

Mathlab将多项式表示为行向量，其中的每个元素是按降幂排序的系数，例如p=[p2,p1,p0]表示多项式$p(x)=p_2{x}^2+p_{1}x+p_0$。

多项式$p(x)=4x^5-3x^2+x+1$的表示：

p=[4 0 0 -3 2 1]

2、多项式的计算

根据特定值计算多项式

polyval(p,1)   %计算多项式p，x=1的值，对于上述例子，输出4

以矩阵形式计算多项式

X = [2 4 5; -1 0 3; 7 1 5];
Y = polyvalm(p,X) 
%输出：Y =    
      154360       78561      193065
       49001       24072       59692
      215378      111419      269582

3、多项式的根

（1） 数值根

roots函数
例：创建一个向量以表示多项式 $x^2-x-6$，然后计算多项式的根。

p = [1 -1 -6];
r = roots(p)
% 输出 r=
         3
        -2

poly函数
poly 函数返回具有指定根的多项式。对向量执行运算时，poly 和 roots 为反函数，因此 poly(roots§) 返回 p。

p2 = poly(r)
% 输出 p2 =
     1    -1    -6

对矩阵执行运算时，poly 函数会计算矩阵的特征多项式。特征多项式的根是矩阵的特征值。因此，roots(poly(A)) 和 eig(A) 返回相同的答案（取决于舍入误差、排序和缩放）。

（2）符号根：以符号形式计算多项式

solve函数
计算多项式的根

syms x     % 声明一个符号变量x
s = solve(x^2-x-6)
% 输出 s =
      -2
       3

factor函数
计算多项式各项的因子

F = factor(x^2-x-6)
% 输出 F =
[ x + 2, x - 3]

（3）求特定区间内的根

使用 fzero 函数求多项式在特定区间内的根。例如，创建一个函数句柄以表示多项式 。

p = @(x) 3*x.^7 + 4*x.^6 + 2*x.^5 + 4*x.^4 + x.^3 + 5*x.^2;

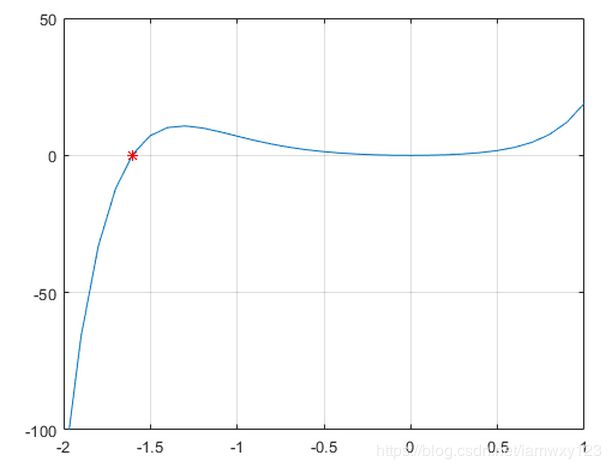
在区间 [-2，1]内绘制该函数。

x = -2:0.1:1;
plot(x,p(x))
ylim([-100 50])
grid on
hold on   

输出：

从绘图中，多项式在 0 和另一个接近 -1.5 的位置各有一个简单的根。使用 fzero 计算并绘制接近 -1.5 的根。

Z = fzero(p, -1.5)     %输出Z=-1.6056
plot(Z,p(Z),'r*')   

4、多项式求微分和积分

1）求微分/求导数
使用 polyder函数获取多项式$p(x)=x^3-2x-5$的导数，生成的多项式为$q(x)=\frac{d}{dx}p(x)=3x^2-2$ 。

p = [1 0 -2 -5];
q = polyder(p)
% 输出
q = 
     3     0    -2

polyder 也可以计算两个多项式积或商的导数。例如，创建两个向量来表示多项式$a(x)=x^2+3x+5$和$b(x)=2x^2+4x+6$ 。
通过调用带有单个输出参数的 polyder来计算两个多项式之积的导数，生成的多项式为$c(x)=8x^3+30x^2+56x+38$。

a = [1 3 5];
b = [2 4 6];
c = polyder(a,b)  
% 输出
c = 
      8    30    56    38

通过调用带有两个输出参数的 polyder来计算两个多项式之商的导数，生成的多项式为：$q(x)=\frac{d}{dx}[\frac{a(x)}{b(x)}]=\frac{-2x^2-8x-2}{4x^4+16x^3+40x^2+48x+36}=\frac{q(x)}{d(x)}$

[q,d] = polyder(a,b) 
% 输出
q =
    -2    -8    -2
d =
     4    16    40    48    36

（2)求微分
使用 polyint函数 对多项式$p(x)=4x^3-3x^2+1$求积分，生成的多项式为 $q(x)=\int p(x)dx=x^4-x^3+x$。

p = [4 -3 0 1];
q = polyint(p)
% 输出
q = 
     1    -1     0     1     0

5、多项式曲线的拟合

此部分说明如何使用polyfit 函数将多项式曲线与一组数据点拟合。按照如下语法，使用 polyfit 求出以最小二乘方式与一组数据拟合的多项式的系数：

   p = polyfit(x,y,n)

其中：

• x 和 y 是包含数据点的 x 和 y 坐标的向量
• n 是要拟合的多项式的次数

举个栗子。

% 包含5个样本点的测试数据（x，y）
x = [1 2 3 4 5]; 
y = [5.5 43.1 128 290.7 498.4];
% 用三次多项式进行拟合，返回结果
p = polyfit(x,y,3)
%输出p= -0.1917   31.5821  -60.3262   35.3400

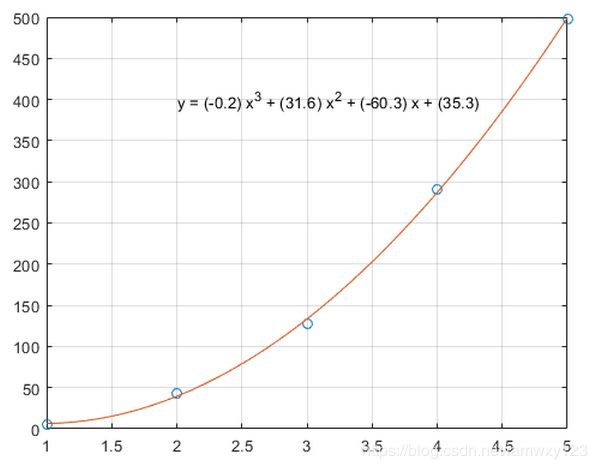
绘制样本点和拟合曲线，输出结果如下图。
x2 = 1:.1:5;
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on
s = sprintf('y = (%.1f) x^3 + (%.1f) x^2 + (%.1f) x + (%.1f)',p(1),p(2),p(3),p(4));
text(2,400,s)