六之再续：KMP算法之总结篇（12.09修订，必懂KMP）

六之再续：KMP算法之总结篇（必懂KMP）

作者：July。
出处：http://blog.csdn.net/v_JULY_v/。

引记

此前一天，一位MS的朋友邀我一起去与他讨论快速排序，红黑树，字典树，B树、后缀树，包括KMP算法，唯独在讲解KMP算法的时候，言语磕磕碰碰，我想，原因有二：1、博客内的东西不常回顾，忘了不少；2、便是我对KMP算法的理解还不够彻底，自不用说讲解自如，运用自如了。所以，特再写本篇文章。由于此前，个人已经写过关于KMP算法的两篇文章，所以，本文名为：KMP算法之总结篇。

本文分为如下六个部分：

1. 第一部分、再次回顾普通的BF算法与KMP算法各自的时间复杂度，并两相对照各自的匹配原理；
2. 第二部分、通过我此前第二篇文章的引用，用图从头到尾详细阐述KMP算法中的next数组求法，并运用求得的next数组写出KMP算法的源码；
3. 第三部分、KMP算法的两种实现，代码实现一是根据本人关于KMP算法的第二篇文章所写，代码实现二是根据本人的关于KMP算法的第一篇文章所写；
4. 第四部分、测试，分别对第三部分的两种实现中next数组的求法进行测试，挖掘其区别之所在；
5. 第五部分、KMP完整准确源码，给出KMP算法的准确的完整源码；
6. 第六部分、一眼看出字符串的next数组各值，通过几个例子，让读者能根据字符串本身一眼判断出其next数组各值。

力求让此文彻底让读者洞穿此KMP算法，所有原理，来龙去脉，让读者搞个通通透透（注意，本文中第二部分及第三部分的代码实现一的字符串下标i 从0开始计算，其它部分如第三部分的代码实现二，第五部分，和第六部分的字符串下标i 皆是从1开始的）。

在看本文之前，你心中如若对前缀和后缀这个两个概念有自己的理解，便最好了。有些东西比如此KMP算法需要我们反复思考，反复求解才行。个人写的关于KMP算法的第二篇文章为：六（续）、从KMP算法一步一步谈到BM算法；第一篇为：六、教你初步了解KMP算法、updated（文末链接）。ok，若有任何问题，恳请不吝指正。多谢。

第一部分、KMP算法初解

1、普通字符串匹配BF算法与KMP算法的时间复杂度比较

KMP算法是一种线性时间复杂的字符串匹配算法，它是对BF算法（Brute-Force，最基本的字符串匹配算法的）改进。对于给的原始串S和模式串P，需要从字符串S中找到字符串P出现的位置的索引。

BF算法的时间复杂度O(strlen(S) * strlen(T))，空间复杂度O(1)。

KMP算法的时间复杂度O(strlen(S) + strlen(T))，空间复杂度O(strlen(T))。

2、BF算法与KMP算法的区别

假设现在S串匹配到i位置，T串匹配到j位置。那么总的来说，两种算法的主要区别在于失配的情况下，对的值做的处理：

BF算法中，如果当前字符匹配成功，即s[i+j] == T[j]，令j++，继续匹配下一个字符；如果失配，即S[i + j] != T[j]，需要让i++,并且j= 0，即每次匹配失败的情况下，模式串T相对于原始串S向右移动了一位。

而KMP算法中，如果当前字符匹配成功，即S[i]==T[j]，令i++，j++，继续匹配下一个字符；如果匹配失败，即S[i] != T[j]，需要保持i不变，并且让j = next[j]，这里next[j] <=j -1，即模式串T相对于原始串S向右移动了至少1位(移动的实际位数j - next[j] >=1),

如果下次匹配是基于T向右移动一位，那么i之前的部分（即S[i-j+1 ~ i-1]），和j=next[j]之前的部分（即T[0 ~ j-2]）仍然相等。显然，相对于BF算法来说，KMP移动更多的位数，起到了一个加速的作用！ (失配的特殊情形，令j=next[j]导致j==0的时候，需要将i ++，否则此时没有移动模式串)。

3、BF算法为什么要回溯

首先说一下为什么BF算法要回溯。如下两字符串匹配（恰如上面所述：BF算法中，如果当前字符匹配成功，即s[i+j] == T[j]，令j++，继续匹配下一个字符）：

i+j（j随T中的j++变，而动）

S：aaaacefghij

j++

T：aaac

如果不回溯的话就是从下一位开始比起：

aaaacefghij

aaac

看到上面红颜色的没，如果不回溯的话，那么从a 的下一位c 比起。然而下述这种情况就漏了（正确的做法当然是要回溯：如果失配，即S[i + j] != T[j]，需要让i++,并且j= 0）：

aaaacefghij

aaac

所以，BF算法要回溯，其代码如下：

int Index(SString S, SString T, int pos) { //返回T在S中第pos个字符之后的位置 i=pos; j=1;k=0; while ( i< = S[0] && j< = T[0] ) { if (S[i+k] = = T[j] ) {++k; ++j;} //继续比较后续字符 else {i=i+1; j=1; k=0;} //指针回溯到 下一首位，重新开始 } if(j>T[0]) return i; //子串结束，说明匹配成功 else return 0; }//Index

不过，也有特殊情况可以不回溯，如下：
abcdefghij(主串)
abcdefg(模式串)
即(模式串)没有相同的才不需要回溯。

4、KMP 算法思想
普通的字符串匹配算法必须要回溯。但回溯就影响了效率，回溯是由T串本身的性质决定的，是因为T串本身有前后'部分匹配'的性质。像上面所说如果主串为abcdef这样的，大没有回溯的必要。

改进的地方也就是这里，我们从T串本身出发，事先就找准了T自身前后部分匹配的位置，那就可以改进算法。

如果不用回溯，那模式串下一个位置从哪里开始呢？

还是上面那个例子，T(模式串)为ababc，如果c失配，那就可以往前移到aba最后一个a的位置，像这样：

...ababd...

ababc

->ababc

这样i不用回溯，j跳到前2个位置，继续匹配的过程，这就是KMP算法所在。这个当T[j]失配后，j 应该往前跳的值就是j的next值，它是由T串本身固有决定的，与S串(主串)无关。

5、next数组的含义

重点来了。下面解释一下next数组的含义，这个也是KMP算法中比较不好理解的一点。

令原始串为: S[i]，其中0<=i<=n；模式串为: T[j]，其中0<=j<=m。

假设目前匹配到如下位置

S0,S1,S2,...,Si-j,Si-j+1...............,Si-1, Si, Si+1,....,Sn

T0,T1,.....................,Tj-1, Tj, ..........

S和T的绿色部分匹配成功，恰好到Si和Tj的时候失配，如果要保持i不变，同时达到让模式串T相对于原始串S右移的话，可以更新j的值，让Si和新的Tj进行匹配，假设新的j用next[j]表示，即让Si和next[j]匹配，显然新的j值要小于之前的j值，模式串才会是右移的效果，也就是说应该有next[j] <= j -1。那新的j值也就是next[j]应该是多少呢？我们观察如下的匹配：

1)如果模式串右移1位（从简单的思考起，移动一位会怎么样），即next[j] = j - 1， 即让蓝色的Si和Tj-1匹配 (注：省略号为未匹配部分)

S0,S1,S2,...,Si-j,Si-j+1...............,Si-1, Si, Si+1,....,Sn

T0,T1,.....................,Tj-1, Tj, .......... (T的划线部分和S划线部分相等【1】)

T0,T1,.................Tj-2,Tj-1, ....... (移动后的T的划线部分和S的划线部分相等【2】)

根据【1】【2】可以知道当next[j] =j -1，即模式串右移一位的时候，有T[0 ~ j-2] == T[1 ~ j-1]，而这两部分恰好是字符串T[0 ~j-1]的前缀和后缀，也就是说next[j]的值取决于模式串T中j前面部分的前缀和后缀相等部分的长度（好好揣摩这两个关键字概念：前缀、后缀，或者再想想，我的上一篇文章，从Trie树谈到后缀树中，后缀树的概念）。

2)如果模式串右移2位，即next[j] = j - 2， 即让蓝色的Si和Tj-2匹配

S0,S1,...,Si-j,Si-j+1,Si-j+2...............,Si-1, Si, Si+1,....,Sn

T0,T1,T2,.....................,Tj-1, Tj, ..........(T的划线部分和S划线部分相等【3】)

T0,T1,...............,Tj-3,Tj-2,.........(移动后的T的划线部分和S的划线部分相等【4】)

同样根据【3】【4】可以知道当next[j] =j -2，即模式串右移两位的时候，有T[0 ~ j-3] == T[2 ~ j-1]。而这两部分也恰好是字符串T[0 ~j-1]的前缀和后缀，也就是说next[j]的值取决于模式串T中j前面部分的前缀和后缀相等部分的长度。

3)依次类推，可以得到如下结论：当发生失配的情况下，j的新值next[j]取决于模式串中T[0 ~ j-1]中前缀和后缀相等部分的长度， 并且next[j]恰好等于这个最大长度。

为此，请再允许我引用上文中的一段原文：“KMP算法中，如果当前字符匹配成功，即S[i]==T[j]，令i++，j++，继续匹配下一个字符；如果匹配失败，即S[i] != T[j]，需要保持i不变，并且让j = next[j]，这里next[j] <=j -1，即模式串T相对于原始串S向右移动了至少1位(移动的实际位数j - next[j] >=1),

同时移动之后，i之前的部分（即S[i-j+1 ~ i-1]），和j=next[j]之前的部分（即T[0 ~ j-2]）仍然相等。显然，相对于BF算法来说，KMP移动更多的位数，起到了一个加速的作用！ (失配的特殊情形，令j=next[j]导致j==0的时候，需要将i ++，否则此时没有移动模式串)。”

于此，也就不难理解了我的关于KMP算法的第二篇文章之中：“当匹配到S[i] != P[j]的时候有 S[i-j…i-1] = P[0…j-1]. 如果下面用j_next去匹配，则有P[0…j_next-1] = S[i-j_next…i-1] = P[j-j_next…j-1]。此过程如下图3-1所示。

当匹配到S[i] != P[j]时，S[i-j…i-1] = P[0…j-1]：

S: 0 … i-j … i-1 i …

P: 0 … j-1 j …

如果下面用j_next去匹配，则有P[0…j_next-1] = S[i-j_next…i-1] = P[j-j_next…j-1]。
所以在P中有如下匹配关系（获得这个匹配关系的意义是用来求next数组）：

P: 0 … j-j_next .…j-1_ …

P: 0 … .j_next-1 …

所以，根据上面两个步骤，推出下一匹配位置j_next:

S: 0 … i-j … i-j_next … i-1 i …

P: 0 … j_next-1 j_next …

图3-1 求j-next（最大的值）的三个步骤

下面，我们用变量k来代表求得的j_next的最大值，即k表示这S[i]、P[j]不匹配时P中下一个用来匹配的位置，使得P[0…k-1] = P[j-k…j-1]，而我们要尽量找到这个k的最大值。”。

根据上文的【1】与【2】的匹配情况，可得第二篇文章之中所谓的k=1（如aaaa的形式），根据上文的【3】与【4】的匹配情况，k=2（如abab的形式）。

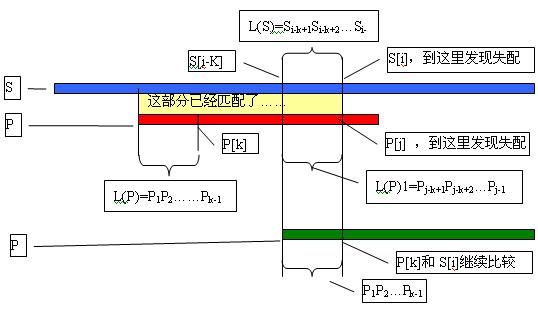
再次总结下，如下图：

从上图中我们看到，当S移动到i，P到j的时候失配。这时候i不回朔，而只是将P向前移动尽可能的距离，继续比较。

假设，P向右移动一定距离后，第k个字符P[k]和S[i]进行比较。 此时如上图，当P[j]和S[i]失配后，i不动，将P前移到K，让P[k]和S[i]继续匹配。现在的关键是K的值是多少？

通过上图，我们发现，因为黄色部分表示已经匹配了的结果（因为是到了S[i]和P[j]的时候才失配，所以S_i-j+1S_i-j+2…S_i-1= P₁P₂…P_j-1，见黄色的部分）。所以有：

1、S_i-k+1S_i-k+2…S_i-1= P_j-k+1P_j-k+2…P_j-1。

所以当P前移到K时，有：

2、S_i-k+1S_i-k+2…S_i-1= P₁P₂…P_k-1。

通过1，2=>

P_j-k+1P_j-k+2…P_j-1= P₁P₂…P_k-1。

而P₁P₂…P_{k-1和Pj-k+1Pj-k+2…Pj-1就相当于P串的前缀和后缀，前已说过，你心中一定要有前缀和后缀的概念或意识。}

所以，归根究底，KMP算法的本质便是：每一次匹配都是基于前一次匹配的结果，如何更好地利用这前一次匹配的结果呢？针对待匹配的模式串的特点，判断它是否有重复的字符，从而找到它的前缀与后缀，进而求出相应的Next数组，最终根据Next数组而进行KMP匹配。接下来，进入本文的第二部分。

第二部分、next数组求法的来龙去脉与KMP算法的源码

本部分引自个人此前的关于KMP算法的第二篇文章：六之续、由KMP算法谈到BM算法。前面，我们已经知道即不能让P[j]=P[next[j]]成立成立。不能再出现上面那样的情况啊！即不能有这种情况出现：P[3]=b，而竟也有P[next[3]]=P[1]=b。

正如在第二篇文章中，所提到的那样：“这里读者理解可能有困难的是因为文中，时而next，时而nextval，把他们的思维搞混乱了。其实next用于表达数组索引，而nextval专用于表达next数组索引下的具体各值，区别细微。至于文中说不允许P=P[next[j] ]出现，是因为已经有P=b与S匹配败，而P[next]=P1=b，若再拿P[1]=b去与S匹配则必败。”--六之续、由KMP算法谈到BM算法。

又恰恰如上文中所述：“模式串T相对于原始串S向右移动了至少1位(移动的实际位数j - next[j] >=1)”。

ok，求next数组的get_nextval函数正确代码如下：

//代码4-1 //修正后的求next数组各值的函数代码 void get_nextval(char const* ptrn, int plen, int* nextval) { int i = 0; nextval[i] = -1; int j = -1; while( i < plen-1 ) { if( j == -1 || ptrn[i] == ptrn[j] ) //循环的if部分 { ++i; ++j; //修正的地方就发生下面这4行 if( ptrn[i] != ptrn[j] ) //++i，++j之后，再次判断ptrn[i]与ptrn[j]的关系 nextval[i] = j; //之前的错误解法就在于整个判断只有这一句。 else nextval[i] = nextval[j]; } else //循环的else部分 j = nextval[j]; } }

举个例子，举例说明下上述求next数组的方法。
S a b a b a b c
P a b a b c
S[4] != P[4]
那么下一个和S[4]匹配的位置是k=2(也即P[next[4]])。此处的k=2也再次佐证了上文第3节开头处关于为了找到下一个匹配的位置时k的求法。上面的主串与模式串开头4个字符都是“abab”，所以，匹配失效后下一个匹配的位置直接跳两步继续进行匹配。
S a b a b a b c
P a b a b c
匹配成功

P的next数组值分别为-1 0 -1 0 2

next数组各值怎么求出来的呢?分以下五步：

1. 初始化：i=0，j=-1，nextval[0] = -1。由于j == -1，进入上述循环的if部分，++i得i=1，++j得j=0，且ptrn[i] != ptrn[j]（即a！=b）），所以得到第二个next值即nextval[1] = 0；；
2. i=1，j=0，进入循环esle部分，j=nextval[j]=nextval[0]=-1；
3. 进入循环的if部分，++i，++j，i=2，j=0，因为ptrn[i]=ptrn[j]=a,所以nextval[2]=nextval[0]=-1；
4. i=2, j=0, 由于ptrn[i]=ptrn[j],再次进入循环if部分，所以++i=3，++j=1,因为ptrn[i]=ptrn[j]=b,所以nextval[3]=nextval[1]=0；
5. i=3,j=1,由于ptrn[i]=ptrn[j]=b,所以++i=4，++j=2,退出循环。

这样上例中模式串的next数组各值最终应该为:

图4-1 正确的next数组各值
next数组求解的具体过程如下：
初始化：nextval[0] = -1，我们得到第一个next值即-1.

图4-2 初始化第一个next值即-1

i = 0，j = -1，由于j == -1，进入上述循环的if部分，++i得i=1，++j得j=0，且ptrn[i] != ptrn[j]（即a！=b）），所以得到第二个next值即nextval[1] = 0；

图4-3 第二个next值0

上面我们已经得到，i= 1，j = 0，由于不满足条件j == -1 || ptrn[i] == ptrn[j]，所以进入循环的esle部分，得j = nextval[j] = -1；此时，仍满足循环条件，由于i = 1，j = -1，因为j == -1，再次进入循环的if部分，++i得i=2，++j得j=0，由于ptrn[i] == ptrn[j]（即ptrn[2]=ptrn[0]，也就是说第1个元素和第三个元素都是a），所以进入循环if部分内嵌的else部分，得到nextval[2] = nextval[0] = -1；

图4-4 第三个next数组元素值-1

i = 2，j = 0，由于ptrn[i] == ptrn[j]，进入if部分，++i得i=3，++j得j=1，所以ptrn[i] == ptrn[j]（ptrn[3]==ptrn[1]，也就是说第2个元素和第4个元素都是b），所以进入循环if部分内嵌的else部分，得到nextval[3] = nextval[1] = 0；

图4-5 第四个数组元素值0
如果你还是没有弄懂上述过程是怎么一回事，请现在拿出一张纸和一支笔出来，一步一步的画下上述过程。相信我，把图画出来了之后，你一定能明白它的。
然后，我留一个问题给读者，为什么上述的next数组要那么求?有什么原理么?

提示：我们从上述字符串abab 各字符的next值-1 0 -1 0，可以看出来，根据求得的next数组值，偷用前缀、后缀的概念，一定可以判断出在abab之中，前缀和后缀相同，即都是ab，反过来，如果一个字符串的前缀和后缀相同，那么根据前缀和后缀依次求得的next各值也是相同的。

• 5、利用求得的next数组各值运用Kmp算法

Ok，next数组各值已经求得，万事俱备，东风也不欠了。接下来，咱们就要应用求得的next值，应用KMP算法来匹配字符串了。还记得KMP算法是怎么一回事吗?容我再次引用下之前的KMP算法的代码，如下：

//代码5-1 //int kmp_seach(char const*, int, char const*, int, int const*, int pos) KMP模式匹配函数 //输入：src, slen主串 //输入：patn, plen模式串 //输入：nextval KMP算法中的next函数值数组 int kmp_search(char const* src, int slen, char const* patn, int plen, int const* nextval, int pos) { int i = pos; int j = 0; while ( i < slen && j < plen ) { if( j == -1 || src[i] == patn[j] ) { ++i; ++j; } else { j = nextval[j]; //当匹配失败的时候直接用p[j_next]与s[i]比较， //下面阐述怎么求这个值，即匹配失效后下一次匹配的位置 } } if( j >= plen ) return i-plen; else return -1; }

我们上面已经求得的next值，如下：

图5-1 求得的正确的next数组元素各值

以下是匹配过程，分三步：
第一步：主串和模式串如下，S[3]与P[3]匹配失败。

图5-2 第一步，S[3]与P[3]匹配失败
第二步：S[3]保持不变，P的下一个匹配位置是P[next[3]]，而next[3]=0,所以P[next[3]]=P[0]，即P[0]与S[3]匹配。在P[0]与S[3]处匹配失败。

图5-3 第二步，在P[0]与S[3]处匹配失败

第三步：与上文中第3小节末的情况一致。由于上述第三步中，P[0]与S[3]还是不匹配。此时i=3,j=nextval[0]=-1,由于满足条件j==-1，所以进入循环的if部分,++i=4,++j=0,即主串指针下移一个位置，从P[0]与S[4]处开始匹配。最后j==plen，跳出循环，输出结果i-plen=4(即字串第一次出现的位置），匹配成功，算法结束。

图5-4 第三步，匹配成功，算法结束
所以，综上，总结上述三步为：

1. 开始匹配，直到P[3]！=S[3]，匹配失败；
2. nextval[3]=0，所以P[0]继续与S[3]匹配，再次匹配失败；
3. nextval[0]=-1，满足循环if部分条件j==-1，所以，++i，++j，主串指针下移一个位置，从P[0]与S[4]处开始匹配，最后j==plen，跳出循环，输出结果i-plen=4，算法结束。

第三部分、KMP算法的两种实现

代码实现一：

根据上文中第二部分内容的解析，完整写出KMP算法的代码已经不是难事了，如下：

//copyright@2011 binghu and july #include "StdAfx.h" #include #include using namespace std; //代码4-1 //修正后的求next数组各值的函数代码 void get_nextval(char const* ptrn, int plen, int* nextval) { int i = 0; //注，此处与下文的代码实现二不同的是，i是从0开始的（代码实现二i从1开始） nextval[i] = -1; int j = -1; while( i < plen-1 ) { if( j == -1 || ptrn[i] == ptrn[j] ) //循环的if部分 { ++i; ++j; //修正的地方就发生下面这4行 if( ptrn[i] != ptrn[j] ) //++i，++j之后，再次判断ptrn[i]与ptrn[j]的关系 nextval[i] = j; //之前的错误解法就在于整个判断只有这一句。 else nextval[i] = nextval[j]; } else //循环的else部分 j = nextval[j]; } } void print_progress(char const* src, int src_index, char const* pstr, int pstr_index) { cout<= plen ) return i-plen; else return -1; } int main() { std::string src = "aabcabcebafabcabceabcaefabcacdabcab"; std::string prn = "abac"; int* nextval = new int[prn.size()]; //int* next = new int[prn.size()]; get_nextval(prn.data(), prn.size(), nextval); //get_next(prn.data(), prn.size(), next); for( int i = 0; i < prn.size(); ++i ) cout< 运行结果，如下图所示：

代码实现二：

再给出代码实现二之前，让我们再次回顾下关于KMP算法的第一篇文章中的部分内容：

“第二节、KMP算法

2.1、 覆盖函数(overlay_function)

覆盖函数所表征的是pattern本身的性质，可以让为其表征的是pattern从左开始的所有连续子串的自我覆盖程度。比如如下的字串，abaabcaba

可能上面的图令读者理解起来还是不那么清晰易懂，其实很简单，针对字符串abaabcaba

a（-1）b（-1）a（0）a（0）b（1）c（-1）a（0）b（1）a（2）

解释：

1. 初始化为-1
2. b与a不同为-1
3. 与第一个字符a相同为0
4. 还是a为0
5. 后缀ab与前缀ab两个字符相同为1
6. 前面并无前缀c为-1
7. 与第一个字符同为0
8. 后缀ab前缀ab为1
9. 前缀aba后缀aba为2

由于计数是从0始的，因此覆盖函数的值为0说明有1个匹配，对于从0还是从来开始计数是偏好问题，具体请自行调整，其中-1表示没有覆盖，那么何为覆盖呢，下面比较数学的来看一下定义，比如对于序列

a0a1...aj-1 aj

要找到一个k,使它满足

a0a1...ak-1ak=aj-kaj-k+1...aj-1aj

而没有更大的k满足这个条件，就是说要找到尽可能大k,使pattern前k字符与后k字符相匹配，k要尽可能的大，原因是如果有比较大的k存在。

但若我们选择较小的满足条件的k，那么当失配时，我们就会使pattern向右移动的位置变大，而较少的移动位置是存在匹配的，这样我们就会把可能匹配的结果丢失。比如下面的序列，

在红色部分失配，正确的结果是k=1的情况，把pattern右移4位，如果选择k=0,右移5位则会产生错误。计算这个overlay函数的方法可以采用递推，可以想象如果对于pattern的前j个字符，如果覆盖函数值为k

a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
则对于pattern的前j+1序列字符，则有如下可能
⑴ pattern[k+1]==pattern[j+1] 此时overlay(j+1)=k+1=overlay(j)+1
⑵ pattern[k+1]≠pattern[j+1] 此时只能在pattern前k+1个子符组所的子串中找到相应的overlay函数，h=overlay(k),如果此时pattern[h+1]==pattern[j+1],则overlay(j+1)=h+1否则重复(2)过程.

下面给出一段计算覆盖函数的代码：

//copyright@ staurman //updated@2011 July #include "StdAfx.h" #include #include using namespace std; //solve to the next array void compute_overlay(const string& pattern) { const int pattern_length = pattern.size(); int *overlay_function = new int[pattern_length]; int index; overlay_function[0] = -1; for(int i=1;i=0 && pattern[i]!=pattern[index+1]) { index = overlay_function[index]; } if(pattern[i]==pattern[index+1]) { overlay_function[i] = index + 1; } else { overlay_function[i] = -1; } } for(int i=0;i 运行结果如下所示：

2.2、kmp算法
有了覆盖函数，那么实现kmp算法就是很简单的了，我们的原则还是从左向右匹配，但是当失配发生时，我们不用把target_index向回移动，target_index前面已经匹配过的部分在pattern自身就能体现出来，只要动pattern_index就可以了。

当发生在j长度失配时，只要把pattern向右移动j-overlay(j)长度就可以了。

如果失配时pattern_index==0，相当于pattern第一个字符就不匹配，这时就应该把target_index加1，向右移动1位就可以了。

ok，下图就是KMP算法的过程（红色即是采用KMP算法的执行过程）：

（另一作者saturnman发现，在上述KMP匹配过程图中，index=8和index=11处画错了。还有，anaven也早已发现，index=3处也画错了。非常感谢。但图已无法修改，见谅）

KMP 算法可在O（n+m）时间内完成全部的串的模式匹配工作。”

OK，下面此前写的关于KMP算法的第一篇文章中的源码：

//copyright@ saturnman //updated@ 2011 July #include "stdafx.h" #include #include #include using namespace std; int kmp_find(const string& target,const string& pattern) { const int target_length=target.size(); const int pattern_length=pattern.size(); int* overlay_value=new int[pattern_length]; overlay_value[0]=-1; //remember:next array's first number was -1. int index=0; //next array for (int i=1;i=0 && pattern[index+1]!=pattern[i]) //remember:!= { index=overlay_value[index]; } if(pattern[index+1] == pattern[i]) { overlay_value[i]=index+1; } else { overlay_value[i]=-1; } } //mach algorithm start int pattern_index=0; int target_index=0; while (pattern_index 由于是abc跟ababc匹配，那么将返回匹配的位置“2”，运行结果如所示：

第四部分、测试

针对上文中第三部分的两段代码测试了下，纠结了，两种求next数组的方法对同一个字符串求next数组各值，得到的结果竟然不一样，如下二图所示：

1、两种方法对字符串abab求next数组各值比较（下图左边为代码实现一内求next数组方法的结果，右边为代码实现二内求next数组方法的结果）：

2、两种对字符串abaabcaba求next数组各值比较（下图左边为代码实现一内求next数组方法的结果，右边为代码实现二内求next数组方法的结果）：

为何会这样呢，其实很简单，上文中已经有所说明了，代码实现一的i 是从0开始的，代码实现二的i 是从1开始的。但从最终的运行结果来看，暂时还是以代码实现段二为准。

第五部分、KMP完整准确源码

求next数组各值的方法为：

//copyright@ staurman //updated@2011 July #include "StdAfx.h" #include #include using namespace std; //solve to the next array void compute_overlay(const string& pattern) { const int pattern_length = pattern.size(); int *overlay_function = new int[pattern_length]; int index; overlay_function[0] = -1; for(int i=1;i=0 && pattern[i]!=pattern[index+1]) { index = overlay_function[index]; } if(pattern[i]==pattern[index+1]) { overlay_function[i] = index + 1; } else { overlay_function[i] = -1; } } for(int i=0;i 运行结果入下图所示：abab的next数组各值是-1，-1,0,1，而非本文第二部分所述的-1,0，-1,0。为什么呢？难道是搬石头砸了自己的脚？

NO，上文第四部分末已经详细说明，上处代码i 从0开始，本文第二部分代码i 从1开始。

KMP算法完整源码，如下：

//copyright@ saturnman //updated@ 2011 July #include "stdafx.h" #include #include #include using namespace std; int kmp_find(const string& target,const string& pattern) { const int target_length=target.size(); const int pattern_length=pattern.size(); int* overlay_value=new int[pattern_length]; overlay_value[0]=-1; //remember:next array's first number was -1. int index=0; //next array for (int i=1;i=0 && pattern[index+1]!=pattern[i]) { index=overlay_value[index]; } if(pattern[index+1] == pattern[i]) { overlay_value[i]=index+1; } else { overlay_value[i]=-1; } } //mach algorithm start int pattern_index=0; int target_index=0; while (pattern_index 运行结果如下：

第六部分、一眼看出字符串的next数组各值

上文已经用程序求出了一个字符串的next数组各值，接下来，稍稍演示下，如何一眼大致判断出next数组各值，以及初步判断某个程序求出的next数组各值是不是正确的。有一点务必注意：下文中的代码全部采取代码实现二，即i是从1开始的。

• 1、对字符串aba求next数组各值，各位可以先猜猜，-1，...，aba中，a初始化为-1，第二个字符b与a不同也为-1，最后一个字符和第一个字符都是a，所以，我猜其next数组各值应该是-1，-1,0，结果也不出所料，如下图所示：

• 2、字符串“abab”呢，不用猜了，我已经看出来了，当然上文中代码实现一和代码实现二都已经求出来了。如果i 是1开始的话，那么next数组各值将如代码实现二所运行的那样，将是：-1，-1,0,1；
• 3、字符串“abaabcaba”呢，next数组如上第三部分代码实现二所述，为-1，-1,0,0,1，-1,0,1,2；
• 4、字符串“abcdab”呢，next数组各值将是-1，-1，-1，-1,0,1；
• 5、字符串“abcdabc”呢，next数组各值将是-1，-1，-1，-1,0,1,2；
• 6、字符串“abcdabcd”呢，那么next数组各值将是-1，-1，-1，-1,0，1,2,3；

怎么样，看出规律来了没？呵呵，可以用上述第五部分中求next数组的方法自个多试探几次，相信，很快，你也会跟我一样，不用计算，一眼便能看出某个字符串的next数组各值了。如此便恭喜你，理解了next数组的求法，KMP算法也就算是真真正正彻彻底底的理解了（至于如何运用求得的next数组各值来进行kmp算法的匹配的具体方法与过程，请转到本文第二部分。不过，需要你注意的是，本文第二部分的i 是从0开始的）。完。

相关链接

1. KMP之第二篇文章：六（续）、从KMP算法一步一步谈到BM算法。
2. KMP之第一篇文章：六、教你初步了解KMP算法、updated。

我的微博

在结束全文之前，引用下自个微博上（@周磊July， http://weibo.com/julyweibo）的两段话：

1. 语言->数据结构->算法：语言是基础，够啃一辈子，基本的常见的数据结构得了如指掌，最后才是算法。除了算法之外，有更多更重要且更值得学习的东西（最重要的是，学习如何编程）。切勿盲目跟风，找准自己的兴趣点，和领域才是关键。这跟选择职位、与领域并持久做下去，比选择公司更重要一样。选择学什么东西不重要，重要的是你的兴趣。
2. 修订这篇文章之时，个人接触KMP都有一年了，学算法也刚好快一年。想想阿，我弄一个KMP，弄了近一年了，到今天才算是真正彻底理解其思想，可想而知，当初创造这个算法的k、m、p三人是何等不易。我想，有不少读者是因为我的出现而想学算法的，但不可急功近利，切勿妄想算法速成。早已说过，学算法先修心。

以下是发自本人微博上的对此书：MySQL性能调优与架构设计，简朝阳著，做的读书笔记，聊做书斋录，以供闲时翻翻：

1. Hash索引在MySQL中使用并不多，目前在Memory和NDB Cluster存储引擎使用。所谓Hash索引，实际上就是通过一定的Hash算法，将须要索引的键值进行Hash运算，然后将得到的Hash值存入Hash表中。检索时，根据Hash表中的Hash值逆Hash运算反馈原键值；
2. InnoDB存储引擎的B-Tree索引使用的存储结构实际上是B+Tree，在B-Tree的基础上做了很小的改造，在每一个LeafNode上除了存放索引键的相关信息，还存储了指向与该LeafNode相邻的后一个LeafNode的指针，此举为了加快检索多个相邻LeafNode的效率；
3. 在我的那篇 从B树、B+树、B*树谈到R 树的文章中介绍到了B树与B+树的差别，B+树的叶子节点中除了跟B树一样包含了关键字的信息之外，还包含了指向相邻叶子节点的指针，如此，叶子节点之间就有了联系、有序了。而B*树则更进一筹，兄弟节点间指针；
4. 无处不透露着数据结构、与算法思想，数据库也不例外。尤其当涉及到数据库性能优化，则更是如此；
5. 又喝了半碗白酒，吃完火锅，叼根烟，同学的手艺实在太好了。来北京初带的钱也即将马上用完了，工作一时还无法定。多亏了同学。再趁着微微酒力，提个问题：我们知道，Hash索引的效率比B-Tree高很多，而为什么大家都不用Hash索引而还要使用B-Tree索引呢?稳定?你能说出几个原因呢?

后记

相信，看过此文后，无论是谁，都一定可以把KMP算法搞懂了（但万一还是有读者没有搞懂，那怎么办呢？还有最后一个办法：把本文打印下来，再仔细琢磨。如果是真真正正想彻底弄懂某一个东西，那么必须付出些代价。但万一要是打印下来了却还是没有弄懂呢？那来北京找我吧，我手把手教你。祝好运）。

OK，扯远了。本文文中有关任何问题或错误，烦请不吝赐教与指正。谢谢，完。

July、二零一一年十二月五日中午。

---

updated：读者Challenge_C_PlusPlus我觉得您还需提炼一下问题的实质。一个KMP算法，说白了就记住一点“构造最大后缀长度数组”，记住这一点，即使实际招聘让我们写这个算法也是可以写出来的。这个KMP讲得太长了，应该可以再精简很多，简而明白。

没错，本文也确实写得太过繁杂冗余了，更的确可以精简，我有负读者了，sorry，严重致歉。July、二零一二年五月十八日。