核心思想:将一个数组进行排序,可以先(递归)将他分成两半分别排序,然后把结果合并起来.若将两个有序表合并成一个有序表,称为二路归并
即:将数组分成两部分,左边部分,和右边部分分别递归再次分成两部分知道每个数组里面只有一个元素.然后调用合并函数,将两个数组进行排好序.每次排序的时候会使用同一个临时缓存,储存排好序的元素.最后的排序结果是 依次把 左半边的 数组 两两排序合并,递归再把合并的数组继续两两合并,最后左边的数组全部合并;接下来对右半部分的数组两两排序合并,重复左边的类似动作,把右边的数组排序成一个数组;最后进行左右两个有序数组合并,组成最终有序数组.
归并排序的时间复杂度是NlogN,缺点是所需要的额外辅助空间和N成正比(需要分配一个与N长度一致的临时存储空间).
2.2.1原地归并的抽象方法:
因为考虑到直接归并算法每次合并需使用一个临时空间,所以考虑在原始数组上直接进行排序,先对前半部分排序,在对后半部分排序.但是相对二路归并的复杂度高.
2.2.2二路归并具体的算法思路:(是一种自顶向下的mergesort)
1.判断需要进入递归操作的边界值.(一般 left
3.进行左半边数组递归调用.直到 left=right ,不在递归.此时提取出数组的第一个元素
4.进行右半边数组递归调用.
5.调用merge方法,把两个有序数组合并.合并的时候会使用一个临时数组.合并的思路是从两个有序的数组第一个元素开始,依次比较,把数据按从小到大的顺序存放到临时temp;遇到某一个数组完成了,剩下一个数组还没比较完,则把剩下的数组复制到temp尾部.最后把temp数组读取,替换实际数组中.
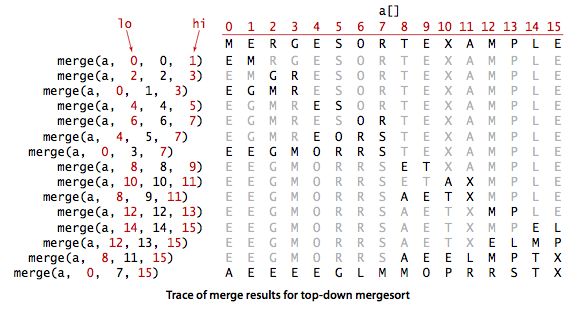
步骤如下图:
要把a[]分成a[lo...hi]两部分,进行分别对 a[lo...mid] ,a[mid+1...hi]进行递归调用,直到调用的数组lo和hi相同时跳出,继而进行和右边部分合并排序.
代码如下:
public class Mergesort{
public static int [] temp;
public void sort(int[] arr){
if(arr==null||arr.lenth==0){
return;}
temp=new int[arr.lenth];
mergesort(arr,0,arr.lenth-1);
}
private void mergsort(int[] arr,int low,int high){
if(low>=high){return;}
int mid=(low+high)/2;
mergesort(arr,low,mid);
mergesort(mid+1,high);
merge(arr,low,mid,high);
}
private void merge(int[] arr,int low,int mid,int high){
int leftIndex=low;
int rightIndex=mid+1;
int tempIndex=0;
while(leftIndex<=mid&&rightIndex<=high){
if(arr[leftIndex]时间复杂度计算:
因为递归算法的时间复杂度可以表示为T(n)=2T(n/2)+O(n).
这是一个每次分一半的递归,总共执行排序的步骤可以画成一棵类似的树.
因为每一层的子问题时间代价为cn,一共有log2N+1 层,所以所有的时间=cn(lgN+1)=cnlnN+cn 时间复杂度
O(NlgN).
命题F:
对于长度为N的任意数组,自顶向下归并排序的需要 ½NlgN ≤O≤ NlgN次比较.
命题G:
对于长度为N的任意数组,自顶向下归并排序最多要访问数组6NlgN次.
证明:
每次归并最多需要访问数组6N次(2N 复制,2N用来将排好序的数组复制过去,2N次进行合并),根据命题F,可知需要有NlgN次比较,所以访问数组为6NlgN.
2.2.3对自定向下的归并排序的优化
1.对小规模的数组使用插入排序.(具体设置的阀值7) 一般插入排序处理小规模排序(例如15)可以将归并缩短时间10%~15%
2.测试数组是否已经有序.在merge之前添加一个方法判断arr[mid]≤arr[mid+1],如果是的话说明这个从lo ...high的数组已经是有序了
3.在merge的时候不进行多次复制.(不把数组复制到临时数组,然后又进行把临时数组的数据copy到src中,这里面至少要经过2次重复操作)优化对临时数组的空间上面还是保持不变,主要在与减少时间.
代码如下:
public class MergeSort{
private static final int OFF_CUT=7;
public void sort(int[] src){
int[] org=src.clone();
mergeSort(org,src,0,org.length-1);
}
private void mergeSort(int[] src,int[] dst,int lo,int hi){
//进行阀值判断
if(hi=src[mid]){
System.arrayCopy(src,lo,dst,lo,hi-lo+1);
}
merge(src,dst,lo,mid,hi);
}
private void insertSort(int[] arr,int lo,int hi){
for(int i=lo+1;i<=hi;i++){
int temp=arr[i];
int j=i;
while(j>lo&&tempmid){
dst[i]=src[hiIndex++];
}else if(hiIndex>hi){
dst[i]=src[lowIndex++];
}else if (src[lowIndex] 2.2.4自底向上的归并排序
使用归并排序的另一种方法是 先归并那些微型数组,然后在归并得到的子数组,反复;直到我们得到整个数组并归并一起.这样比标准递归方法需要的代码更少.
[手摇算法,又称三次反转]
用于反转字符串包括里面有不服顺序改变,可以将空间复杂度降低至O(1).
具体做法.例子:
题目要求部分反转数组。比如说1,2,3,4,5 翻转后是3,4,5,1,2
class Reverse{
private void reverse(int[] a, int low, int hi) {
while (low < hi) {
swap(a, low, hi);
low++;
hi--;
}
}
//这里也用到内存反转3次 进行交换两个数 ,采用 ^操作
private void swap(int[] a, int left, int right) {
a[left] ^= a[right];
a[right] ^= a[left];
a[left] ^= a[right];
}
public static void main(String[] args) {
int[] test = {1, 2, 3, 4, 5};
Reversel rev=new Reverse();
rev.reverse(test, 0, 1);
rev.reverse(test, 2, test.length - 1);
rev.reverse(test, 0, test.length - 1);
for (int i = 0; i < test.length; i++) {
System.out.print(test[i]);
}
}
}
自底向上,的归并排序的思路是
- 先分割成前半部分为1,后半部分的数组, 划分成 N/2 段.
- 然后接着以分成前半部分为2,后半部分为2的数组.
- 然后接着以分成前半部分为3,后半部分为3的数组.
… - 直到每部分的步长接近N 或者超过N.
/**
* Created by leon on 18-1-24.
* 这里是采用自底向上的算法
*/
public class MergeSortBottom2Up {
public void sort(int[] arr) {
System.out.println("自底向上递归前:" + Arrays.toString(arr));
int num = arr.length;
//翻倍递增
for (int i = 1; i < num; i = i + i) {
for (int j = 0; j < num; j++) {
int low = Math.min(j, num - 1);
j = j + i + i - 1;/*往后移动步长*/
int high = Math.min(j, num - 1);
int mid = (low + high) / 2;
merge(arr, low, mid, high);
}
}
System.out.println("自底向上递归后:" + Arrays.toString(arr));
}
/**
* 进行在一个数组里面for循环,发现lowIndex下标超过mid 或者 highIndex 超过high进行切换
* 比较的思路:
* 1.lowIndex=lo,midIndex,highIndex=mid+1
* 1.从lowIndex 开始 ++,比较src[lowIndex] 和 src[highIndex]的值,直到 src[lowIndex]>src[highIndex]停止
* 2.用midIndex 定位到highIndex
* 3.从highIndex++,直到src[highIdex]>src[lowIndex],停
* 此刻说明从 midIndex~highIndex-1的数比lowIndex的小,需要插入到lowIndex之前.
* 利用内存3次反转(手摇技术)反转内存,达到把midIndex~highIndex-1部分插入到lowIndex之前
* ____________________
* |1|3|4|5|9|10|2|6|7|
* `^``````````^`^``````
* l h =>初始 l,m,h=m+1
* ____________________
* |1|3|4|5|9|10|2|6|7|
* ```^````````^`^````
* l h =>移动l,arr[l]>arr[h]
* ____________________
* |1|3|4|5|9|10|2|6|7|
* ```l``````````m`h``` =>把m->h位置,h++,直到arr[h]>arr[l]
*此时说明 arr[m]~arr[h-1]的数小于 arr[l],需要进行3次内存反转,
*达到把arr[m]~arr[h-1]排到arr[lowIndex]前面
* ____________________
* |1|3|4|5|9|10|2|6|7|
*
* ____________________
* |1|10|9|5|4|3|2|6|7|==> 反转左边
^ ^ ^
* ____________________
* |1|10|9|5|4|3|2|6|7|==>反转右边 只有一个 2
* ^ ^ ^
* ____________________
* |1|2|3|4|5|9|10|6|7|==>反转两部分
* ^ ^ ^
*完成一次排序,
* lowIndex=lowIndex+i+i-1;继续下一次排序
*
* @param src
* @param lo
* @param mid
* @param hi
*/
private void merge(int[] src, int lo, int mid, int hi) {
int lowIndex = lo;
int highIndex = mid + 1;
//当 lowIndex 与highIndex 重叠时.或者highIndex超出了最外层结束
while (lowIndex < highIndex && highIndex <= hi) {
while (lowIndex < highIndex && src[lowIndex] <= src[highIndex]) {
lowIndex++;
}
int midIndex = highIndex;
//这里的边界值很关键
while (highIndex <= hi && src[highIndex] < src[lowIndex]) {
highIndex++;
}
Convert(src, lowIndex, midIndex - 1, highIndex - 1);
//完成一次排序
lowIndex += highIndex - midIndex;
}
}
void Convert(int a[], int low, int M, int high) {
//反转 low...middle
reverse(a, low, M);
//反转middle+1 high
reverse(a, M + 1, high);
//反转low...high
reverse(a, low, high);
}
private void reverse(int[] a, int low, int hi) {
while (low < hi) {
swap(a, low, hi);
low++;
hi--;
}
}
private void swap(int[] a, int left, int right) {
a[left] ^= a[right];
a[right] ^= a[left];
a[left] ^= a[right];
}
}
2.2.5 排序算法的复杂度
研究复杂度的第一步是建立模型.一般来说寻找与问题相关的最简单的模型.排序算法,是基于主键的比较决定的.
命题I:
没有任何基于比较的算法能够保证使用少于lg(N!)~NlogN次比较将长度为N的数组排序.
这个结论告诉我们在设计排序时能达到的最佳效果.
命题J:
归并排序是一种渐进最优的基于比较的排序算法.更准确的说.归并排序在最坏情况下的比较次数和其他基于比较的任意算法的最少时间都是~NlogN.