jzoj4447 【HNOI2016模拟4.14】A (维护凸壳，分段函数)

题面

分析

分开每个点求，显然一条最短路能作用很久。同一条最短路作用的部分我们是可以直接计算的。
先求出长度为k的最短路
随着时间增长，每一条路的长度都可以表示为一个一次函数
y=w+Lenx 。
于是问题就变成了一次函数求凸壳。

---

首先我们将所有直线按w从小到大排序，然后考虑一开始两条直线，按顺序记作 l1,l2 。

现在要插入一条直线 l3 ，

Case0

若 l3 比上一条直线的斜率要大，显然是不需要考虑的。

Case1

这条直线与 l1 的交点横坐标大于 l1,l2 交点，这样的话 l3 需要考虑。

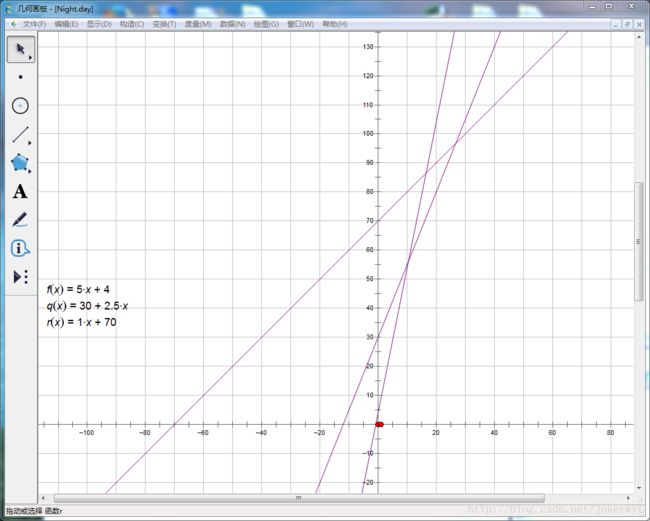
Case2

这条直线与 l1 的交点横坐标小于等于 l1,l2 交点。这时我们发现 l2 直接会被 l3 盖过去，于是并不需要考虑 l2 了。 (下面这张图有点问题，l3的截距应该大于等于l2)

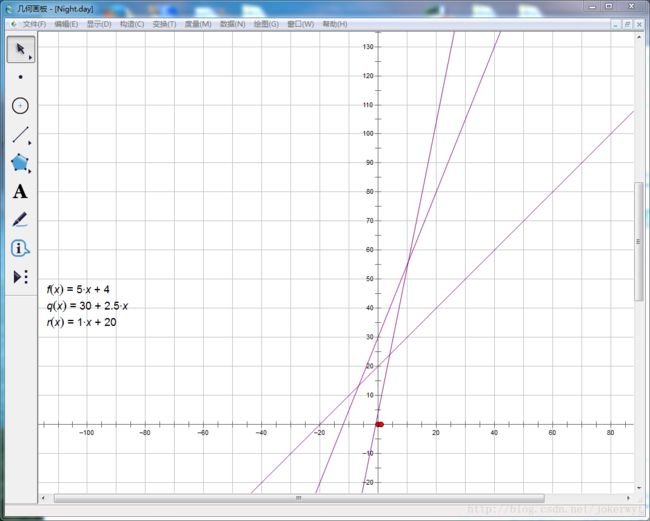
基于上述讨论，我们可以用一个单调栈，维护栈中所有直线与前一直线的交点递增。

最后再根据得出来的凸壳分段计算就可以了。时间复杂度 O(n2logn)

优化：发现有很多显然不会有贡献的直线，我们可以改一下 f[i][j] 的定义，变为至多j条边，而不是恰好j条边。 也就是对 f[i][j−1] 取个min。这样出来的f[i]就是单调的，而且显然相同的一段第一个的最优。 渐进复杂度并不会改变，但常数小.

再考虑一种维护方法：直接按斜率从大到小插入，复杂度减小一个log
没有仔细的讨论过，但应该大同小异。（有一些特殊情况?）

---

Code

#include 
#include 
#include 
#include 
#include 
#define N 2510
#define M N*N*2
#define min(a,b) ((a)<(b)?(a):(b))
#define mo 1000000007ll
#define dc(x,y) ((((x)+(y))%mo*((y)-(x)+1)%mo+mo)*500000004ll%mo)
#define get(j) ((b[j].w-b[j-1].w)/(double)(b[j-1].len-b[j].len))
using namespace std;
typedef long long ll;
struct P{
    ll len,w;
    P(ll llen=0,ll ww=0) {len=llen,w=ww;}
};
bool cmp(P a,P b) {
    return a.wint from[M],to[M],head[N],next[M],w[M],tot;
int n,m,t;
ll f[N][N*2],vis[N][N];
P a[N],b[N];
void link(int x,int y,int v) {
    to[++tot]=y; from[tot]=x;
    next[tot]=head[x];
    head[x]=tot; w[tot]=v;
}
void dp() {
    memset(f,127,sizeof f);
    f[1][0]=0;
    for (int len=1; len<=n; len++) {
        for (int j=1; j<=tot; j++) {
            int x=from[j],y=to[j];
            f[y][len]=min(f[y][len-1],f[y][len]);
            f[y][len]=min(f[y][len],f[x][len-1]+w[j]);
        }
    }
}

int main() {
    //freopen("2.in","r",stdin);
    cin>>n>>m>>t;

    for (int i=1; i<=m; i++) {
        int u,v,l; scanf("%d %d %d",&u,&v,&l);
        link(u,v,l); link(v,u,l);
    }
    ll sum=0; double temp;
    dp();
    for (int i=2; i<=n; i++) {
        int cnta=0;
        for (int j=1; j<=n; j++) if (f[i][j]!=f[0][0] && f[i][j]!=f[i][j-1]) a[++cnta]=P(j,f[i][j]);
        sort(a+1,a+1+cnta,cmp); 
        int cnt=0;  b[++cnt]=a[1];
        if (cnta>=2 && a[2].len2];

        for (int j=3; j<=cnta; j++) {
            double tmp;
            while (cnt>=2 && get(cnt)>=(tmp=(a[j].w-b[cnt-1].w)/(double)(b[cnt-1].len-a[j].len)) && tmp>=0) cnt--;
            if (a[j].lenint ls=0;
        if (cnt==1) {
            sum=(sum+(t+1)*b[1].w%mo+dc(0,t)*b[1].len%mo)%mo;
            continue;
        } else 
        for (int j=2; j<=cnt; j++) {
            ll xt=min(t+1,ceil(get(j)));
            sum=(sum+(xt-1-ls+1)*b[j-1].w%mo+ dc(ls,xt-1)*b[j-1].len)%mo;
            ls=xt;
        }
        if (ls<=t) sum=(sum+(t-ls+1)*b[cnt].w+ dc(ls,t)*b[cnt].len)%mo;
    }
    cout<