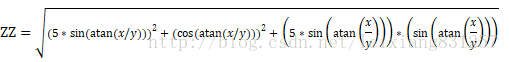基于JMP的神经网络设计案例分析
基于JMP的神经网络设计案例分析
摘 要:本文利用JMP对一个复杂多项式进行拟合,从实验设计产生样本数据、神经网络设计、训练样本技巧、到结果分析进行详细阐述。使读者能够使用JMP软件的神经网络分析工具,解决实际问题。
关键词:神经网络,JMP,数据分析
1.引言
当前人工智能已经应用在很多领域,辅助人类解决了很多问题,神经网络作为人工智能的基础理论,近些年也得到飞速发展,也有了TensorFlow、Caffe、Chainer等机器学习框架,能够满足用户快速搭建应用。本文使用JMP软件提供的神经网络工具,对一个复杂多项式进行拟合,并对结果进行分析,便于提升大家对神经网络的直观认识。JMP是全球最大的统计学软件公司SAS推出了一种交互式可视化统计发现软件,被誉为“卓越绩效的统计发现引擎”,其主要有三个特点,一是具有操作简便、交互性强、可视化效果好的特点,专业版中还集成了预测、聚类、质量与过程、可靠性与生存、消费者研究等分析工具,适合非统计专业背景的数据分析人员使用,二是JMP还有强大的实验设计功能,几乎涵盖了所有主流的实验设计工具。三是提供强大的二次开发功能,JMP可以作为一个服务器引擎,提供调用接口,实现用户个性化需求,为用户节省大量复杂设计和计算。
2.样本产生
神经网络的样本数据是基础,为了能够进行直观喝准确的对比神经网络的学习效果,使用下述多项式产生样本数据,再利用神经网络进行学习训练。
使用JMP进行可视化,得到图1,显示了对应Z的效果。
图1 多项式可视化效果图
使用JMP的实验设计功能,对曲面进行抽样,为了计算快速,使用空间填充设计的快速灵活填充设计方法,输入需要的样本数量,即可均匀产生样本空间。
图2 通过JMP实验设计得出1000个样本点。
产生样本点以后,使用多项式进行计算,得出进行学习的样本点,神经网络通过学习样本数据,拟合出模型。(注:使用该多项式,目的是为了产生准确的样本数据,神经网络中不需要这个多项式模型)。
3.神经网络的设计
神经网络本质是高维模型的拟合,也是一种回归思想,找一个模型来对多维数据进行拟合,但这个模型不是经典的线性模型、二次模型、或者指数模型等,而是一组矩阵参数,通过修改参数来使得样本值与实际值的误差最小,或者误差稳定。在JMP中,设计神经网络结构主要是要设计隐层的数量和每一层的节点数量。理论上节点和层数越多,拟合效果越好,但是层数和节点越多,计算量越大,容易导致过拟合。JMP中提供了2个隐藏层、三种激活函数,可以根据具体情况进行选择和设计。
图3 JMP中神经网络工具界面
3.1设计基本原则
首先确定网络层数、然后确定节点个数。网络层次在大多数情况下,使用1个隐藏就够,不宜太多。节点个数一般从3个开始,不断增加,如果维度比较多,那么节点个数一般要大于维度,后面层次的节点个数不宜太多。这些原则并没有什么科学依据,都是同行的经验。
然后是训练结果分析,通过观察测试误差,是否达到我们的精度要求来衡量神经网络的优劣,是否需要改进。训练结果中主要关注训练集和验证集的R平方这个指标,被称为判定系数,是衡量拟合效果的重要参数。R平方的范围是[0,1] ,越趋近1,说明拟合效果越好,越趋近与0,效果越差。另外,还可以把预测值与实际值进行可视化比较,直观比较预测效果。
最后,修正网络结构。通过多次训练,循环迭代修正网络结构,使得网络达到最稳定状态。
3.2 设计案例
为了对比各种设计的优劣,根据JMP提供的实验环境,下面进行三组实验。
实验一:使用1000个样本数据进行学习训练结果,其中验证集是使用了其中20%的样本作为交叉验证,为便于对比,设定随机数种子。下面实验主要是验证各种激活函数的性能、以及节点数量对拟合效果的影响。
表1 不同激活函数、节点数量对拟合效果数据
| 次数 |
激活函数 |
隐藏层数 |
第一层 节点个数 |
第二层 节点个数 |
训练集 R平方 |
测试集 R平方 |
| 1 |
TanH |
1 |
3 |
0 |
0.8651 |
0.8554 |
| 2 |
恒等线性 |
1 |
3 |
0 |
0.0006 |
0.0018 |
| 3 |
径向高斯 |
1 |
3 |
0 |
0.9347 |
0.9241 |
| 4 |
TanH |
1 |
5 |
0 |
0.9498 |
0.9407 |
| 5 |
恒等线性 |
1 |
5 |
0 |
0.2095 |
0.1945 |
| 6 |
径向高斯 |
1 |
5 |
0 |
0.9652 |
0.9653 |
| 7 |
TanH |
1 |
7 |
0 |
0.9596 |
0.9473 |
| 8 |
恒等线性 |
1 |
7 |
0 |
0.0003 |
0.0005 |
| 9 |
径向高斯 |
1 |
7 |
0 |
0.9726 |
0.9750 |
| 10 |
TanH |
1 |
9 |
0 |
0.9771 |
0.9559 |
| 11 |
恒等线性 |
1 |
9 |
0 |
0.0008 |
0.0017 |
| 12 |
径向高斯 |
1 |
9 |
0 |
0.9873 |
0.9841 |
| 13 |
TanH |
1 |
11 |
0 |
0.9764 |
0.9791 |
| 14 |
恒等线性 |
1 |
11 |
0 |
0.0008 |
0.0017 |
| 15 |
径向高斯 |
1 |
11 |
0 |
0.9914 |
0.9851 |
| 16 |
TanH |
1 |
13 |
0 |
0.9802 |
0.9849 |
| 17 |
恒等线性 |
1 |
13 |
0 |
0.0003 |
0.0008 |
| 18 |
径向高斯 |
1 |
13 |
0 |
0.9937 |
0.9856 |
为了便于对比,使用JMP的图形生成器,对上述表格进行叠加可视化,效果如图
图4 三种激活函数、节点数量对拟合效果的对比。
图中我们可以看出,使用线性的激活函数效果最差,即使是节点数量增加,也没有明显提升,对于TanH和径向高斯两张激活函数无明显差异,径向高斯激活函数相对比较稳定,当节点数量增加到一定程度后,无明显差异。
实验二:从实验一中 可以看出线性激活函数的拟合能力很差,不适合本实验样本,因此下属实验只使用其余两种激活函数。JMP提供了2个隐层设计,下面的实验中,增加一个隐藏层。
表2 使用2个隐层结构后不同节点数量拟合效果数据
|
|
激活函数 |
隐藏层数 |
第一层 节点个数 |
第二层 节点个数 |
训练集 R平方 |
测试集 R平方 |
| 1 |
TanH |
2 |
3 |
3 |
0.9372 |
0.9321 |
| 2 |
径向高斯 |
2 |
3 |
3 |
0.9711 |
0.9827 |
| 3 |
TanH |
2 |
3 |
4 |
0.9909 |
0.9849 |
| 4 |
径向高斯 |
2 |
3 |
4 |
0.9347 |
0.9241 |
| 5 |
TanH |
2 |
3 |
5 |
0.9915 |
0.9943 |
| 6 |
径向高斯 |
2 |
3 |
5 |
0.9974 |
0.9979 |
| 7 |
TanH |
2 |
3 |
6 |
0.9923 |
0.9911 |
| 8 |
径向高斯 |
2 |
3 |
6 |
0.9903 |
0.9906 |
| 9 |
TanH |
2 |
3 |
7 |
0.9975 |
0.9971 |
| 10 |
径向高斯 |
2 |
3 |
7 |
0.9367 |
0.9966 |
实验三:交换两个隐层节点的数量,观察对拟合度的影响
表3 交换2个隐层点数量拟合效果数据
|
|
激活函数 |
隐藏层数 |
第一层 节点个数 |
第二层 节点个数 |
训练集 R平方 |
测试集 R平方 |
| 1 |
TanH |
2 |
3 |
3 |
0.9372 |
0.9321 |
| 2 |
径向高斯 |
2 |
3 |
3 |
0.9711 |
0.9827 |
| 3 |
TanH |
2 |
4 |
3 |
0.9670 |
0.9723 |
| 4 |
径向高斯 |
2 |
4 |
3 |
0.9347 |
0.9241 |
| 5 |
TanH |
2 |
5 |
3 |
0.9920 |
0.9913 |
| 6 |
径向高斯 |
2 |
5 |
3 |
0.9980 |
0.9987 |
| 7 |
TanH |
2 |
6 |
3 |
0.9820 |
0.9736 |
| 8 |
径向高斯 |
2 |
6 |
3 |
0.9963 |
0.9947 |
| 9 |
TanH |
2 |
7 |
3 |
0.9941 |
0.9953 |
| 10 |
径向高斯 |
2 |
7 |
3 |
0.9972 |
0.9949 |
从表2、3中我们可以看出,R平方的值是随节点的数量增加而增加,但节点增加到一定数量后,R平方的值变化不大,因此在设计节点数量时,当R平方的值稳定到一定范围后,就没有必要再继续增加节点数量,因为节点数量增加,会导致后期学习训练的运算量成急剧增加。隐藏层节点的数量交换后,对结果影响不大。
图5 两种激活函数、节点数量对拟合效果叠加对比
从图5中可以看出,在本实验中当R平方到达0.99后,基本趋于稳定。所以,我们确定网络层的节点第一层位5个,第二层为3个,网络结构如下图6.
图6 网络结构
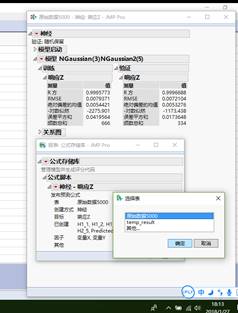
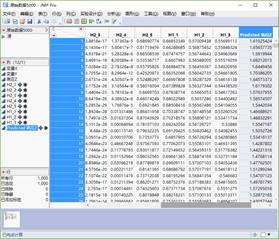
网络结构确定后,就可以使用神经网络的模型进行预测和分析。在JMP里面,训练结束后,点击模型左边的红色小三角,点击“发布预测公式”,在出来的对话框中,点击神经左边的红色小三角,点击“运行脚本”,选择数据对话框,预测出来的结果,就保存在当前现在的数据表后面几列,列名加上了“Predicted”前缀。
图7 JMP中使用神经网络模型进行预测示意图
4.神经网络结论分析
有了预测数据和真是数据,可以使用JMP中提供的“叠加图”来进行可视化分析,右图中“+”符号表示预测结果,“O”表示实际结果,从图中可以看出,大部分点都比较吻合,说明预测效果良好。
图7 JMP中使用叠加图对比预测结果和实际结果示意图
为了更加直观看到神经网络的预测效果,还可以用JMP提供的曲面图工具,对真实值和预测值进行可视化,观察二者的效果,如图8,作图为实际多项式的可视化效果,右图为通过神经网络学习后预测出来的效果。
图8 JMP中使用叠加图对比预测结果和实际结果示意图