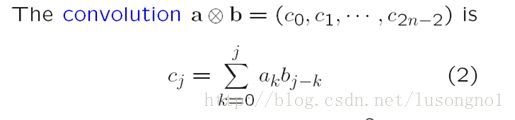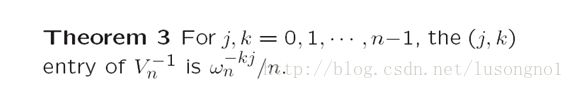从多项式乘法来看快速傅里叶变换

从多项式乘法来看快速傅里叶变换

如果要列举二十一世纪最伟大十大算法，我想FFT是榜上有名的。不论你是数学系还是计算机系的学生，不管你是学理论的还是搞应用的，我想，你都应该懂点快速傅里叶变换。

---

多项式乘法

假定有两个多项式，如下：

A(x)=a0+a1x+⋯+an−1xn−1

B(x)=b0+b1x+⋯+bn−1xn−1

问A和B做乘法得到C要怎么做。自然而然地想到的是：

• 直接乘，然后合并同类项，头脑稍微清楚一点，也可说先找C的常数项，再找 x 前面的系数，最后到 x2n−2 ，前面的系数，这意味着要做n方次乘法和n成n-1次加法和 (n−2)∗(n−1)/2 次的加法，整体的运算量为 O(n2) 。

• 在A和B上找2n-1个点的函数值，做乘法后得到C的2n-1个点的函数值，然后通过插值得到C的表达式。我们知道有m+1个点可以唯一地插值一个m多项式，这是插值告诉我们的。那么用常规做法，这件事情复杂度几何？

  1、使用Horner方法计算多项式在一点的值的运算是n的量级的：
  

  2、求得A和B若干点值后相加，运算量自然是n的量级的。

  3、通过插值将2n-1个点还原为多项式C，它的运算量是也是 O(n2) 。比如说就用拉格朗日插值，用A插值做比，C也一样：

  

也就是说搞了半天，运算数量级依然是n方的，第二种方法好像还更麻烦一点，干嘛还要说第二种方法呢。
事实上，我们我们可以通过选择合适地插值节点，通过合适的方法，可以大大减小第二种方法的运算量。这个方法呢，就是快速傅里叶变换。它的运算量，大概是 O(nlog(n)) 。

---

在使用傅里叶变换方法来改进第二种方法进行多项式乘法之前，我们需要先介绍一下离散卷积和离散傅里叶变换。

卷积

不难发现我们前面提到的多项式乘法第一种方法，其实就是A的系数和B的系数做卷积得到C的系数。即多项式乘法，其实是关于系数的卷积运算。摆公式，下标整来整去似乎难记又会错乱，我是这样理解的：

ci=(a0,a1,...ai)⋅(bi,bi−1,...b0)  i=0,...n−1

ci=(ai−n+1...an−1)⋅(bn−1,bn−2,...bi−n+1)  i=n,...,2n−2

也就是说 ci 开始的时候等于 a0 到 ai 和 b0 到 bi 的反向做内积，一直到延长到最后，然后固定 an−1 从第一项开始减，并和 b 想对应的位置反向做内积直到最后 an−1∗bn−1 ……有没有点像毛毛虫走路的感觉？好吧，我承认我说得有点抽象。事实上，这更像是两列相向行驶的火车，从头碰头的那一刻，到尾对尾离开的那一刻，火车的长度任意，还可以是无限长……卷积的每一项就是取火车重叠部分的乘积和，也就是重叠部分对应每辆火车的一个向量然后做内积，这不作为重点，就不画图说明了……

---

离散傅里叶变换（DFT）

以上图片表示的就是离散傅里叶变换和逆变换，看起来非常抽象，不过没关系，容我解释解释。比如说我们现在要将长度为n的向量 (a0⋯an−1) 通过傅里叶变换，变成长度为m的一个向量要怎么操作呢？很简单。
将复平面的单位圆周m等分，等分点记为：

ω0m,ω1m,⋯,ωm−1m

我们分别以这m个数作为比值，可以做m个等比数列，每个等比数列的长度都是n，把这m个等比数列和原来的a向量做内积，就得到了傅里叶变换后的向量。

是的，可能明眼人已经看出来了，所谓的离散傅里叶变换，其实就是把这个n个等分点代入以 ai 为系数的多项式A（如前所示），而得到的一列向量。可能这样会更好理解一点。

写成矩阵乘法，如下所示：

这里其实默认m等于n了。

离散傅里叶变换矩阵的逆，是由以下定理来保证的：

---

利用FFT进行多项式乘法

前面已经提到了多项式乘法实际上就是系数之间做卷积，作为新的多项式的系数。

有一条定理，说的是：卷积的傅里叶变换等于傅里叶变换的乘积。
这就意味做多项式的乘法我们可以这样操作：把两个多项式的系数做傅里叶变换后相乘，将得到的结果做傅里叶逆变换，就能得到乘积多项式的系数。

因为离散傅里叶变换对应着将若干单位圆周上的点代入多项式，且傅里叶逆变换事实上也就意味着为对单位圆周上点值的插值还原，那么上述操作其实说的就是开篇提到的做多项式乘法的第二种方法，只是插值节点选择的是复平面上的，且比较特殊的点。

当然，如果只是单纯地去做离散傅里叶变换，本质上还是前面提到的第二种方法，只是插值节点选得比较特殊，复杂度还是n方量级的，并没有什么太大作用。这时候快速傅里叶变换就登场了，它能大大减少离散傅里叶变换（包括逆变换）过程中的运算量。

简单地说，因为所选的插值节点具有“等比”这种特殊的性质，我们在计算函数在某一点的值时，进行了很多重复的操作。我们可以通过一些手段减少这种重复的工作：将多项式 按奇数项和偶数项分成两把，奇数那一半提出一个x之后内部长得就和偶数那一部分长得一样，然后将 x2 看成一个未知变量，那么插值节点纷纷平方以后，数量减少了一倍，再做离散傅里叶变换，大约只需要一半的工作量，不仅如此，在计算傅里叶变换后半部分值时，所做的工作其实很大一部分也是在重复在计算前半部分值时所做的工作。

通过递推关系：

我们能算出快速傅里叶变换求解多项式乘法工作量为 nlog2n+nC 。

这个依次一分为二，再用傅里叶变换，这是一个递归的过程，给出一个伪代码描述这个过程：

以上说的就是一维的卷积和傅里叶变换，以及其和多项式乘法之间的一个关系。一维的卷积和FFT可以推广到高维，这里就不说了。好了，我要说的就这么多。下面给出上课用的PPT，仅供参考。

不管是知乎还是各大博客平台，网上有着各种各样对快速傅里叶变换的通俗讲解。可是，越是通俗的比喻，懂的人默默一笑，刚入门的人还是一头雾水。既然你查了，相信你对这个东西的背景应用等有一定的了解。我写博客的宗旨是：尽量不说废话，能用汉字说清楚思想的，绝不用公式。