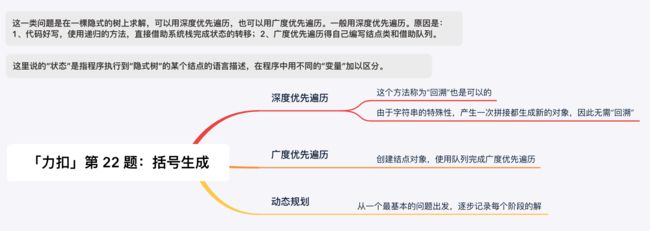
Leetcode22. Generate Parentheses
Leetcode22. Generate Parentheses
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
解法一 深度优先遍历
我们以 n = 2 为例,画树形结构图。方法是 “做减法”。
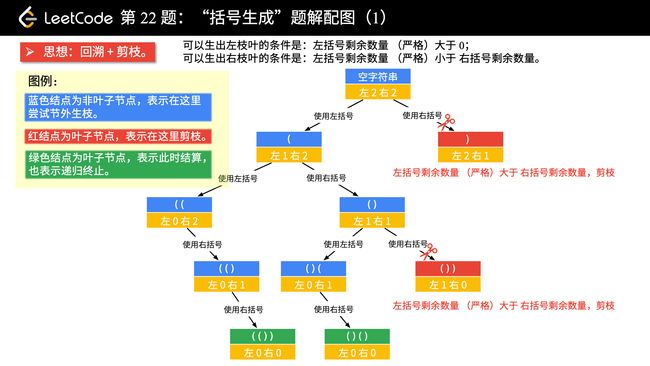
可以分析出:
-
当前左右括号都有大于 0 个可以使用的时候,才产生分支;
-
产生左分支的时候,只看当前是否还有左括号可以使用;
-
产生右分支的时候,还受到左分支的限制,右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候,才可以产生分支;
-
在左边和右边剩余的括号数都等于 0 的时候结束。
public class Solution {// 做减法,1ms
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
if (n == 0) {
return res;
}
dfs("", n, n, res);// 执行深度优先遍历,搜索可能的结果
return res;
}
/**
* @param curStr 当前递归得到的结果
* @param left 左括号还有几个可以使用
* @param right 右括号还有几个可以使用
* @param res 结果集
*/
private void dfs(String curStr, int left, int right, List<String> res) {
// 因为每一次尝试,都使用新的字符串变量,所以无需回溯
// 在递归终止的时候,直接把它添加到结果集即可,注意与「力扣」第 46 题、第 39 题区分
if (left == 0 && right == 0) {
res.add(curStr);
return;
}
// 剪枝(如图,左括号可以使用的个数严格大于右括号可以使用的个数,才剪枝,注意这个细节)
if (left > right) {
return;
}
if (left > 0) {
dfs(curStr + "(", left - 1, right, res);//对应树中的左子树
}
if (right > 0) {
dfs(curStr + ")", left, right - 1, res);//对应树中的右子树
}
}
}
class Solution:
# @param {integer} n
# @return {string[]}
def generateParenthesis(self, n):
if not n:
return []
left, right, ans = n, n, []
self.dfs(left,right, ans, "")
return ans
def dfs(self, left, right, ans, string):
if right < left:
return
if not left and not right:
ans.append(string)
return
if left:
self.dfs(left-1, right, ans, string + "(")
if right:
self.dfs(left, right-1, ans, string + ")")
dfs(2, 2, [], "")
dfs(1, 2, [], "(")
dfs(0, 2, [], "((")
dfs(0, 1, [], "(()")
dfs(0, 0, [], "(())") # We got "(())" and we append it to ans
dfs(1, 1, ["(())"], "()")
dfs(0, 1, ["(())"], "()(")
dfs(0, 0, ["(())"], "()()") # We got "(())" and we append it to ans
dfs(1, 0, ["(())", "()()"], "())") # will just return as right < left
dfs(2, 1, ["(())", "()()"], ")") # will just return as right < left
回溯(与深度优先相似)
public List<String> generateParenthesis(int n) {//做加法
List<String> list = new ArrayList<String>();
backtrack(list, "", 0, 0, n);
return list;
}
//结果集,递归得到的结果,左括号数,右括号数,最大n
public void backtrack(List<String> list, String str, int open, int close, int max){
if(str.length() == max*2){//如果已经有2n个括号,则加入结果集
list.add(str);
return;
}
if(open < max)//左括号只要有就可以加入
backtrack(list, str+"(", open+1, close, max);
if(close < open)//右括号加入的前提是左括号数目比右括号大
backtrack(list, str+")", open, close+1, max);
}
解法二 动态规划
第 1 步 定义状态
dp[i]表示使用i对括号能够生成的组合
注意:每一个状态都是列表的形式。
第 2 步:思考状态转移方程
dp[i] = "(" + dp[可能的括号对数] + ")" + dp[剩下的括号对数]
- 可能的括号对数” 与 “剩下的括号对数” 之和得为
i - 1,“可能的括号对数”j取值为[0,i-1] - “剩下的括号对数” =
i - j - 1
dp[i] = "(" + dp[j] + ")" + dp[i- j - 1] , j = 0, 1, ..., i - 1
第 3 步:考虑初始化
dp[0] = [""]
第 4 步:考虑输出
d[n]
public List<String> generateParenthesis(int n) {
if (n == 0) {
return new ArrayList<>();
}
// 这里 dp 数组我们把它变成列表的样子,方便调用而已
List<List<String>> dp = new ArrayList<>(n);
List<String> dp0 = new ArrayList<>();
dp0.add("");
dp.add(dp0);
for (int i = 1; i <= n; i++) {
List<String> cur = new ArrayList<>();
for (int j = 0; j < i; j++) {
List<String> str1 = dp.get(j);
List<String> str2 = dp.get(i - 1 - j);
for (String s1 : str1) {
for (String s2 : str2) {
// 枚举右括号的位置
cur.add("(" + s1 + ")" + s2);
}
}
}
dp.add(cur);
}
return dp.get(n);
}
class Solution(object):
def generateParenthesis(self, n):
"""
:type n: int
:rtype: List[str]
"""
dp = [[] for i in range(n + 1)]
dp[0].append('')
for i in range(n + 1):
for j in range(i):
dp[i] += ['(' + x + ')' + y for x in dp[j] for y in dp[i - j - 1]]
return dp[n]
To generate all n-pair parentheses, we can do the following:
1. Generate one pair: ()
2. Generate 0 pair inside, n - 1 afterward: () (...)...
Generate 1 pair inside, n - 2 afterward: (()) (...)...
...
Generate n - 1 pair inside, 0 afterward: ((...))
更多解法
有注释的dp
Python trick