计算机网络复习笔记第十部分--加密(英文版本)
Cyrptograhy
- Encryption and Decryption
- traditional cryptography
- substitution代替 cipher (Caesar cipher)
- transposition cipher 转移密码
- Product cipher
- modern cryptography
- DES(data encryption standard)
- Merkle's puzzles and Shamir's method
- public key encryption
- RSA algorithm
- digital signature
- message digest (MD)
Encryption and Decryption
encryption model
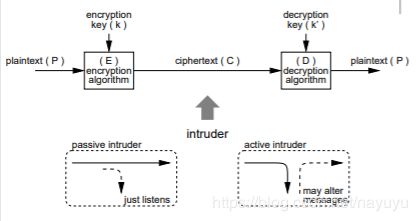
Encryption:
an encryption process E (with an encryption key k, E角标k) transforms a plaintext P to a ciphertext C: C=Ek ( P )
Decryption
a decryption process D (with a decryption key k’) transforms the ciphertext C to the original message P: P = Dk’ ( C )
– E and D are just mathematical algorithms
– often k = k’
traditional cryptography
substitution代替 cipher (Caesar cipher)
basic idea is replacement between bits
Plaintext: ‘the caesar cipher fooled the carthaginians’
- shifting each alphabet by k. 假如k=1,每个字母都往后挪一个。 a→ B, b→ C, . . ., z→ A, 码字变成‘ UIF DBFTBS DJQIFS GPPMFE UIF DBSUIBHJOJBOT ’
- mapping alphabets randomly to others, a→ Q, b→ W, c→ E, . . .码字变成‘ ZIT EQTLQK EOHITK YGGSTR ZIT EQKZIQUOFOQFL ’
- (a bit more complex) mapping all ASCII characters randomly to others.
Ciphertext: ‘ ZIT EQTLQK EOHITK YGGSTR ZIT EQKZIQUOFOQFL ’
– 26!∼4× 1026 possible keys exist for random alphabet mapping — at 1µ(sec) per key, 1000 machines will solve in 1010 years.
– in fact, not difficult to break by exploiting the statistical properties of natural language — e.g., for English,

are most common.
Breaking the subsititution cipher: ‘ ZIT EQTLQK EOHITK YGGSTR ZIT EQKZIQUOFOQFL ’
- frequent letters: Q (5 times), T (5), I (4), E (3), K (3), O (3), Z (3), .=⇒ they may be substitutions for ‘ e, t, o, a, n, i ’.
- a trigram三字母组: ZIT (twice) =⇒ possibly ‘ the ’.
- here is one guess: Z→ t, I→ h, T→ e, Q→ a, O→ i, ‘ the EaeLaK EiHheK YGGSeR the EaKthaUiFiaFL ’
- and this ‘guessing game’ continues for the rest, using further statistical clues.
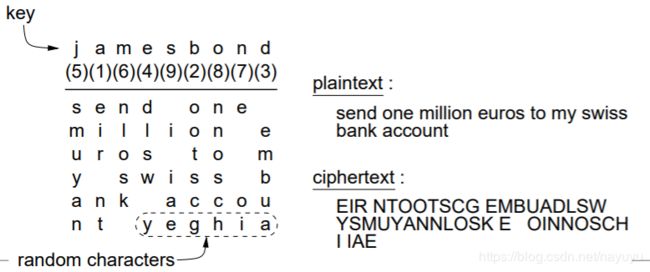
transposition cipher 转移密码
basic idea is rearrangement of bits
how to do this cipher:
- choose a key k to number the columns
- write the plaintext in rows
- read the ciphertext by columns, starting with the column whose key letter is the lowest.
breaking the transposition cipher:
- find a cipher ⇐ test the statistical pattern
if there are many e, t, o, a, n, i, it is more likely to be a transposition cipher than a substitution cipher. - find # columns ⇐ guess for contents of message
we suppose ‘swiss bank account’ to occur and this cipher to have nine columns, bigrams such as sk, ia, sc, bu, an, nt may appear. - order the columns ⇐ test the statistical pattern
– first we choose two columns that fit best to the bigram pattern of plaintext
– then we find the third column that fits best to the bigram/trigram patterns (continue for all columns)
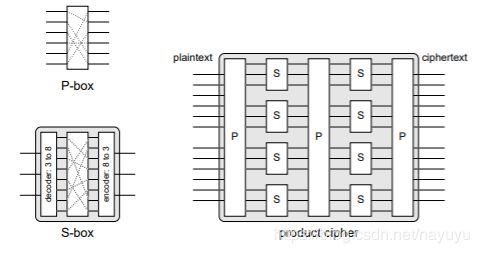
Product cipher
combination of elements to build complex ciphers
modern cryptography
compare modern and traditional cryptography:
- traditional cryptography: uses simple algorithms, but relies on long keys in order to make ciphertxt more cryptic
- modern cryptography: keeps the keys short, but uses complex procedures to encrypt data
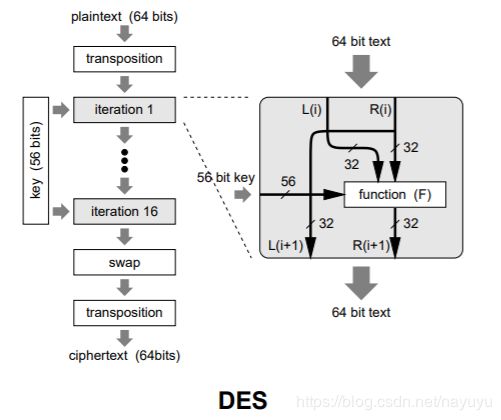
DES(data encryption standard)
- key is 56 bits length
- plaintext is encrypted in blocks of 64-bits, yielding 64-bits of ciphertext
- 19 stages includes 16 functionally identical iterations迭代
- decryption is done with the same 56-bit key, but run in reverse order
breaking the DES— suppose a small piece of plaintext and matched ciphertext is given:
- can design a machine that does exhaustive search (256∼7.2× 1016 keys) in less than one day.
- national lottery attack
– ten million people own a TV set, installed with a DES chip芯片 that does only one million encryptions per second (very cheap).
– once a plaintext/ciphertext pair is broadcasted, each of ten million chips begins searching preassigned section of key space.
– within two hours, one TV set hits a jackpot and the owner wins a fortune. ⇒ DES cannot be used for anything important.
Brute-force attack
- also known as an exhaustive详尽的 search for discovering keys
- try every combination until the correct key is found
- can be used against most of encrypted data
- often prohibitively过分地 inefficient
- national lottery attack is one example for a brute-force attack
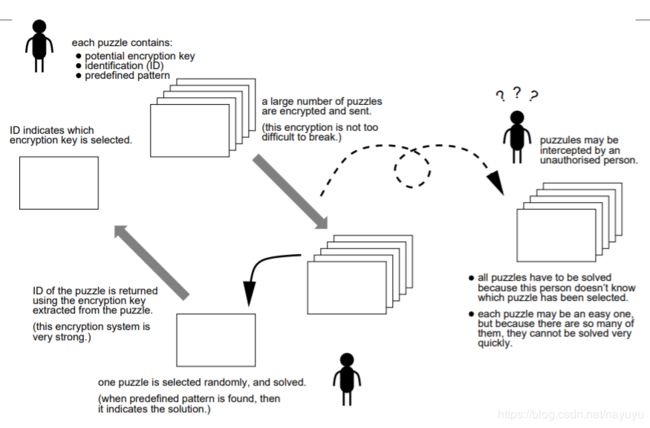
Merkle’s puzzles and Shamir’s method
Merkle’s puzzles
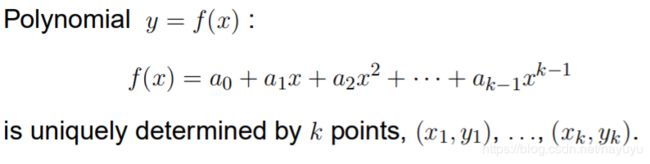
Shamir’s method:
- each of k persons - neither of them knows the key --carries unique data point (xi,yi)
- k points uniquely determine the polynomial, whose coefficients系数 (ai’s) are then used to derive a key
- if less than k persons arrives the destination, a polynomial cannot be uniquely determined, but it is still possible to find a relation between coefficients
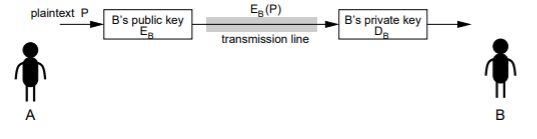
public key encryption
There is no reason encryption algorithm cannot be made public, suppose
- D(E§) =P
where E/D: encryption / decryption algorithms, P: plaintext - it is exceedingly difficult to deduce推论 D from E
Scenario:
- encryption algorithm E with key k is made public, but decryption algorithm D, whose key k ′ is different from k, is kept secret.
- anybody, wishing to send a message, encrypts with E.
- ciphertext cannot be read unless you know D.
RSA algorithm
- parameter selection:
– choose two large primes质数, p and q. (typically greater than 10的100次方)
– compute n = pq, and z = (p-1)(q-1)
– choose a number relatively prime to z and call it d
– find e such that e × d e \times d e×d modz =1 - procedure:
– the pair (e,n) is made public.

– the rest (p,q,z,d) is kept private.

Why is the RSA algorithm secure?
- n is made public , n=pq
- difficult to fatoring large numbers 分解大的数字难
- Estimation — using a computer that makes one calculation per one micro second: factoring 200-digit number requires four billion years ; factoring 500-digit number requires 1025 years
digital signature
‘Signed message’ system签名系统 should satisfy
- authentication of the process: the receiver can verify the claimed声明 identity of the sender
(e.g.) a bank needs a authorised signature for transaction. - protection of message receiver: the sender cannot later change the contents of the message.
(e.g.) a dishonest customer might withdraw money, then sue the bank that he never did such transaction. - protection of the message sender: the receiver cannot forge伪造 the message
(e.g.) a stock broker might buy a junk stock without a customer’s approval.
Secret key signature:
advantage:
- fast and efficient
disadvantage:
- the secret key is required to verify the authenticity of the message, leading to a key distribution problem;
- or find a third party that moderate协调 the communication.
Secret key system:
Public/private key signature:
advantage:
- public keys can be freely and openly distributed分发
disadvantage:
- calculations for encryption/decryption are very costly
signing the message签署消息 using a public/private key system:
- authentication of message
- sender digitally signs a message using the private key
- suppose a public key encryption/decryption algorithm can do E(D§) = P
- of the recipient can decrypt this message using sender’s public key, it is the proof for authenticity真实性 of the sender
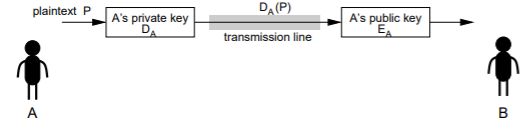
signing and encoding a message using the public/private key system:
- suppose D(E§) = P , E (D§) = P
(e.g.) RSA algorithm has this property - the recipient (‘B’) is sure that
– ‘A’ is the actual sender of the message
– only the recipient can read the message

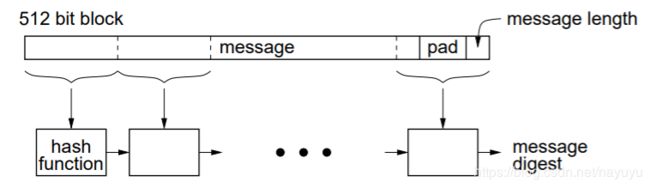
message digest (MD)
- also known as a hash value散列值 (or simply a hash)
- a fixed size, quasi-unique fingerprint generated by a formula from an arbitrary任意值 sized message
- similar in principle to the computation of CRC
- typical digest size of 128 to 256 bits to represent 10的38次方 to 10的77次方 different values
- much less costly than encrypting the entire message
- detection of corrupted message
- protection against unauthorised modification, achieved by encryption. (note) MD alone does not offer any protection
- compute MD from a plaintext P using a hash function
- encrypt MD using the sender’s private key
- send the plaintext P and the encrypted MD
Receiving a message:
- compute MD′ from P using the same hash function
- decrypt MD using the sender’s public key
- compare MD′ with MD
A good hash function:
- efficient to compute MDs
- virtually impossible to find a message having the
identical MD - dependent on every bit of the message
(i.e., two nearly identical messages to have totally different hash values)