狡猾的商人
洛谷P2294 [HNOI2005]狡猾的商人
前言
大概一定是我太蒻了,卡在这道题的差分约束做法上卡了几个小时QAQ
在摸差分约束做法前,得出了类似于这位dalao题解的思路,可惜因为没想到优先队列而选择了\(vector\),所以没有实现(在看了题解之后独自编出来了,会具体讲解)
做法
-
优先队列
-
差分约束系统
(对优先队列那种神奇做法不感兴趣的可以直接跳过看差分约束做法)
优先队列
还是算有点贪心+模拟的思路吧?因为这种做法好像没名字(传说中的玄学孤儿算法qwq)
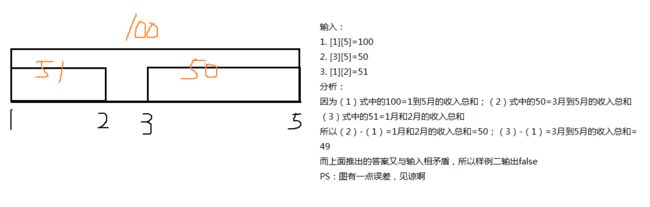
先来分析一波两个样例(直接见图即可):
所以,我们可以得出一种解决方法:
先将输入的区间按规则排序,然后依次比较前后两个区间,遇到左端点相等的就推出另一个式子压入待处理判断的数组中,如果有两个式子相矛盾就直接输出\(false\),否则最后输出\(true\)
排序规则:左端点相等则右端点小的在前,否则按左端点小的排在前
这里我们需要思考一下,因为是前后两个区间比对,所以我们每压入一个新的式子都要进行如上排序。那怎么实现?直接\(sort\)肯定是会超时的
在看了最上面那篇题解后,恍然大悟:直接用重载的优先队列啊!
至于时间复杂度的证明,我也不会,但是优先队列确实比\(sort\)跑得快
放上代码:
#include
using namespace std;
int T,n,m;
struct node {
int u,v,w;
bool operator < (const node &x)const { //重载运算符版的优先队列
if(u!=x.u) return u>x.u;
return v>x.v;
}
} a;
priority_queue q;
int main() {
scanf("%d",&T);
while(T--) {
bool flag=true;
while(!q.empty()) q.pop(); //记得清空
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&a.u,&a.v,&a.w);
q.push(a); //输入一个就压入一个
}
node fir=q.top();
q.pop();
// cout< 差分约束系统
不了解差分约束系统的珂见这篇博客啊qwq 无耻
我们首先需要确定的是这题跑最短路还是最长路
我个人偏向于跑最长路(因为跑最短路似乎也能A?)
为什么是最长路?因为在差分约束系统中跑最长路得到的是最小解(不懂的就上面的链接吧ovo),且如果最小解都满足了那大一点的解肯定也满足
那本题的约束条件是什么?直接是输入中的\(t-s=v\)吗?
当然不是!转换一下思路,从\(s\)到\(t\)的总收入可以用前缀和表示:\(sum[i]\)表示\(i\)月之前的所有月收入的总和
那约束条件则是\(sum[t]-sum[s-1]=v\)!
再转换上面那个式子,就得到如何建边:
-
\(sum[t]-sum[s-1]≥v\),所以从\(t\)到\(s-1\)连一条权值为\(v\)的边
-
\(sum[t]-sum[s-1]≤v\),所以从\(s-1\)到\(t\)连一条权值为\(-v\)的边
然后就是正常的跑差分约束系统的最长路板子了(这里采用全部入队的方式,而不是使用超级源点)
代码如下:
#include
using namespace std;
int T,n,m,u,v,w,tot;
int dis[250010],vis[250010],cnt[250010],head[250010];
struct node {
int to,net,val;
} e[250010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline bool spfa() { //spfa求差分约束系统最长路板子
queue q;
for(register int i=0;i<=n;i++) {
dis[i]=0;
vis[i]=1;
cnt[i]=1;
q.push(i);
}
while(!q.empty()) {
int x=q.front();
q.pop();
vis[x]=0;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v] 然后,感谢一些同桌对我程序的修改
最后,如果这篇题解有任何问题,欢迎在留言区留言,我会及时改正,谢谢qwq