论文阅读理解 - Dilated Convolution

Dilated Convolution

[Paper]: Multi-scale Context Aggregation by Dilated Convolutions

[Caffe-Code]

1. Caffe 中的定义

Dilated Convolution 已经可在 Caffe 官方的卷积层参数中定义.

message ConvolutionParameter {
  // Factor used to dilate the kernel, (implicitly) zero-filling the resulting holes. 
  // (Kernel dilation is sometimes referred to by its use in the
  //  algorithme à trous from Holschneider et al. 1987.)
  repeated uint32 dilation = 18; // The dilation; defaults to 1
}

layer {
  name: "ct_conv1_1"
  type: "Convolution"
  bottom: "fc-final"
  top: "ct_conv1_1"
  param {
    lr_mult: 1
    decay_mult: 1
  }
  param {
    lr_mult: 2
    decay_mult: 1
  }
  convolution_param {
    num_output: 42
    pad: 33
    kernel_size: 3
  }
}
layer {
  name: "ct_relu1_1"
  type: "ReLU"
  bottom: "ct_conv1_1"
  top: "ct_conv1_1"
}
layer {
  name: "ct_conv1_2"
  type: "Convolution"
  bottom: "ct_conv1_1"
  top: "ct_conv1_2"
  param {
    lr_mult: 1
    decay_mult: 1
  }
  param {
    lr_mult: 2
    decay_mult: 1
  }
  convolution_param {
    num_output: 42
    pad: 0
    kernel_size: 3
  }
}
layer {
  name: "ct_relu1_2"
  type: "ReLU"
  bottom: "ct_conv1_2"
  top: "ct_conv1_2"
}
layer {
  name: "ct_conv2_1"
  type: "Convolution"
  bottom: "ct_conv1_2"
  top: "ct_conv2_1"
  convolution_param {
    num_output: 84
    kernel_size: 3
    dilation: 2
  }
}
layer {
  name: "ct_relu2_1"
  type: "ReLU"
  bottom: "ct_conv2_1"
  top: "ct_conv2_1"
}
layer {
  name: "ct_conv3_1"
  type: "Convolution"
  bottom: "ct_conv2_1"
  top: "ct_conv3_1"
  convolution_param {
    num_output: 168
    kernel_size: 3
    dilation: 4
  }
}
layer {
  name: "ct_relu3_1"
  type: "ReLU"
  bottom: "ct_conv3_1"
  top: "ct_conv3_1"
}
layer {
  name: "ct_conv4_1"
  type: "Convolution"
  bottom: "ct_conv3_1"
  top: "ct_conv4_1"
  convolution_param {
    num_output: 336
    kernel_size: 3
    dilation: 8
  }
}
layer {
  name: "ct_relu4_1"
  type: "ReLU"
  bottom: "ct_conv4_1"
  top: "ct_conv4_1"
}
layer {
  name: "ct_conv5_1"
  type: "Convolution"
  bottom: "ct_conv4_1"
  top: "ct_conv5_1"
  convolution_param {
    num_output: 672
    kernel_size: 3
    dilation: 16
  }
}
layer {
  name: "ct_relu5_1"
  type: "ReLU"
  bottom: "ct_conv5_1"
  top: "ct_conv5_1"
}
layer {
  name: "ct_fc1"
  type: "Convolution"
  bottom: "ct_conv5_1"
  top: "ct_fc1"
  convolution_param {
    num_output: 672
    kernel_size: 3
  }
}
layer {
  name: "ct_fc1_relu"
  type: "ReLU"
  bottom: "ct_fc1"
  top: "ct_fc1"
}
layer {
  name: "ct_final"
  type: "Convolution"
  bottom: "ct_fc1"
  top: "ct_final"
  convolution_param {
    num_output: 21
    kernel_size: 1
  }
}

2. Paper - Multi-scale Context Aggregation by Dilated Convolutions

语义分割属于 dense prediction 问题， 不同于图像分类问题.

Dilated Convolutions 能够整合多尺度内容信息，且不损失分辨率，支持接受野的指数增长.

图像分类任务通过连续的 Pooling 和 Subsampling 层整合多尺度的内容信息，降低图像分别率，以得到全局预测输出.

Dense Prediction 需要结合多尺度内容推理(multi-scale contextual reasoning)与 full-resolution 输出.

处理 multi-scale reasoning 与 full-resolution dense prediction 冲突的方法：

• 利用重复的 up-convolutions 操作，重构丢失的分辨率，保留downsampled 层的全局信息.
• 利用图像不同 rescaled 的信息作为网络输入，并结合其输出. 不过无法确定哪个 rescaled 输入图像是最需要的.

Dilated Convolutions 不会降低图像分辨率，或分析 rescaled 图像，整合了多尺度的内容信息. 可以以任何分辨率加入到已有的网络结构中.

2.1 Dilated Convolution

定义离散函数： F:Z2→R F : Z 2 → R ， 假设 Ωr=[−r,r]2⋂Z2 Ω r = [ − r , r ] 2 ⋂ Z 2 ， k:Ω→R k : Ω → R 是大小为 (2r+1)2 ( 2 r + 1 ) 2 的离散 filter. 则离散卷积操作 ∗ ∗ 的定义为：

(F∗k)(p)=∑s+t=p ( F ∗ k ) ( p ) = ∑ s + t = p .

其一般化形式为：

(F∗lk)(p)=∑s+lt=p ( F ∗ l k ) ( p ) = ∑ s + l t = p

其中 l l 为 dilation 因子， ∗l ∗ l 为 dilation convolution. 当 l=1 l = 1 时，即为普通的离散卷积操作 ∗ ∗ .

基于 Dilation Convolution 的网络支持接受野的指数增长，不丢失分辨率信息.

记 F0,F1,...,Fn−1:Z2→R F 0 , F 1 , . . . , F n − 1 : Z 2 → R 为离散函数， k0,k1,...,kn−2:Ω→R k 0 , k 1 , . . . , k n − 2 : Ω → R 是离散的 3×3 3 × 3 fliters， 采用指数增长 dilation 的 filters后，

Fi+1=Fi∗2iki, for i=0,1,...,n−2 F i + 1 = F i ∗ 2 i k i ,   f o r   i = 0 , 1 , . . . , n − 2

定义 Fi+1 F i + 1 中的元素 p p 的接受野为： F0 F 0 中可以改变 Fi+1(p) F i + 1 ( p ) 值的元素集. Fi+1 F i + 1 中 p p 的接受野的大小即为这些元素集的数目.

显而易见， Fi+1 F i + 1 中各元素的接受野大小为 (2i+2−1)×(2i+2−1) ( 2 i + 2 − 1 ) × ( 2 i + 2 − 1 ) . 接受野是指数增长大小的平方.

如图 Figure1.

Figure1：Dilated Convolution例示.

(a) 采用 1-dilated convolution 对 F0 F 0 操作得到的 F1 F 1 ， F1 F 1 中各元素的接受野为 3×3 3 × 3 .

(b) 采用 2-dilated convolution 对 F1 F 1 操作得到的 F2 F 2 ， F2 F 2 中各元素的接受野为 7×7 7 × 7 .

(c) 采用 4-dilated convolution 对 F2 F 2 操作得到的 F3 F 3 ， F3 F 3 中各元素的接受野为 15×15 15 × 15 .

各层的参数数量是相同的. 随着参数的线性增加，接受野指数增长.

2.2 多尺度内容信息聚合(Multi-scale Context Aggreation)

context 模块通过整合多尺度内容信息来提高 dense prediction 的结果. 其输入是 C C 个特征图(feature maps)， 输出也是 C C 个特征图，输入输出的形式相同.

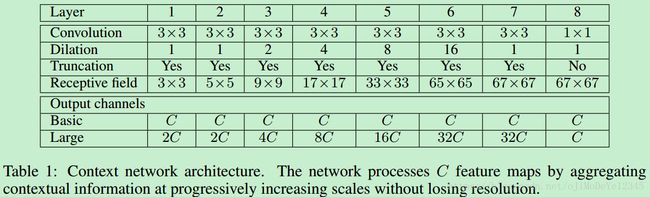
context 模块的基本形式中，各层具有 C C 个 channels. 尽管特征图没有归一化，模块内也没有定义loss，但各层的表示是相同的，可以直接用于获得 dense per-class prediction. 直观上是可以增加特征图的准确度的.

基本的 context 模块有 7 层，各层采用具有不同的 dilation 因子的 3×3 3 × 3 卷积. 各卷积操作后跟着一个逐元素截断(pointwise truncation)操作： max(⋅,0) m a x ( ⋅ , 0 ) . 最终的输出是采用 1×1×C 1 × 1 × C 的卷积操作得到的.

3. Reference

[1] - caffe::ConvolutionLayer

[2] - Multi-scale context aggregation by dilated convolutions

[3] - dilation8_pascal_voc_deploy.prototxt

[4] - 如何理解空洞卷积（dilated convolution）？