题目链接:https://www.jisuanke.com/contest/6516
A:题目:
我们称一个数是质数,而且数位中出现了 5 的数字是有趣的。
例如 5, 59, 457。求1到100000中有趣的数的个数。
题解:无脑分解和暴力枚举素数即可。
代码:
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int mod = 10007;
bool check(int x)
{
int flag = 0;
for (int i = 2; i <= sqrt(x); i++)
if (x % i == 0)
flag = 1;
if (flag == 1)return false;
else return true;
}
bool check2(int x)
{
int t;
while (x != 0)
{
t = x % 10;
x = x / 10;
if (t == 5)return true;
}
return false;
}
int main(void)
{
int num = 0;
for (int i = 2; i <= 100000; i++)
{
if (check(i) == true)
if (check2(i) == true)
num++;
}
cout << num << endl;
return 0;
}
答案:3282
B:题目:
蒜头君要爬楼梯。楼梯一共有10层台阶。
因为腿长的限制,每次最多能上4层台阶。但是第5,7层楼梯坏掉了不能踩。求上楼梯的方案数。
题解:通过上一层转移,没啥坑。
代码:
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int mod = 10007;
int dp[15];
int main(void)
{
dp[1] = 1;
dp[2] = dp[1] + 1;
dp[3] = dp[2] + dp[1] + 1;
dp[4] = dp[3] + dp[2] + dp[1] + 1;
dp[5] = 0;
dp[6] = dp[5] + dp[4] + dp[3] + dp[2];
dp[7] = 0;
for (int i = 8; i <= 10; i++)
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] + dp[i - 4];
cout << dp[10] << endl;
return 0;
}
答案:72
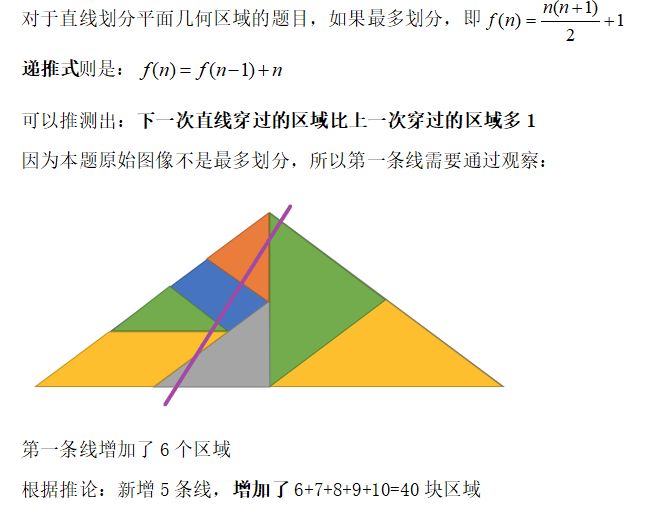
C:题目:求问在以下图案的大三角形内部添加五条直线最多可以将大三角形分成多少个区域。
请在下图的基础上添加五条直线。
题解:
答案:47
D:题目:
有3030个篮子,每个篮子里有若干个苹果,篮子里的苹果数序列已经给出。
现在要把苹果分给小朋友们,每个小朋友要么从一个篮子里拿三个苹果,要么从相邻的三个篮子里各拿一个苹果。(苹果可以剩余)
比如对于序列3 1 3,可以分给两个小朋友变成0 1 0;也可以分给一个小朋友变成2 0 2,此时不能继续再分了。所以答案是2。
求问对于以下序列{7,2,12,5,9,9,8,10,7,10,5,4,5,8,4,4,10,11,3,8,7,8,3,2,1,6,3,9,7,1}最多分给几个小朋友?
题解:本题考虑贪心,贪心的策略是:从左到右取苹果,使浪费的苹果最少。篮子中大于等于3个苹果的直接取3个,取到小于3个为止。然后将此篮子当作1 1 1取法的左端点,继续取,直到无法操作。
这样确保每次都是局部最优,因而推出整体最优。
代码:
#include
#include
#include
using namespace std;
typedef long long ll;
//尽可能少剩下的苹果最少为贪心思路
int main()
{
ios::sync_with_stdio(false);
int sum = 0;
int a[35] = { 0,7,2,12,5,9,9,8,10,7,10,5,4,5,8,4,4,10,11,3,8,7,8,3,2,1,6,3,9,7,1 };
int ans = 0;
for (int i = 1; i <= 30; ++i)
{
ans += a[i] / 3;
a[i] %= 3;
/*
for (int i = 1; i <= 30; i++)
cout << a[i] << " ";
cout << endl;
*/
while (a[i] >= 1 && a[i + 1] >= 1 && a[i + 2] >= 1)
{
a[i]--; a[i + 1]--; a[i + 2]--;
ans++;
}
}
cout << ans << endl;
return 0;
}
答案:62
E:题目:
广场上的小朋友们排成了整齐的方阵。具体来说,我们可以把每个小朋友看做是一个点,那么小朋友们就形成了n×n的点阵。
方阵中,小朋友A和小朋友B互相可以看见,当且仅当二人之间的连线不经过别的小朋友,且他们之间的距离不超过k。我们想知道有多少对小朋友互相可以看见。(A,B)与 (B,A)算同一对。
例如,n=2,k=1时答案为4,n=2,k=2 时答案为6,n=3,k=2时答案为20。
现在我们想要知道,当n=1000,k=500时的答案是多少。由于答案过大,请回答对10^9+7取模后的结果。
分析:本题是填空题中唯一有难度的一问,坑点较多。(ps:用了对拍才找到自己的错误)
题解:
代码:(正确代码)
#include
using namespace std;
typedef long long ll;
const int MOD = 1e9 + 7;
int main()
{
int n, k;
cin >> n >> k;
ll ans = 2 * n * (n - 1) % MOD;//边框上的线数目
for(int x = 1; x <= n; x++)
{
for(int y = 1; y <= n; y++)
{
if(x * x + y * y > k * k)continue;
if(__gcd(x, y) != 1)continue;
ans = (ans + 2 * (n - x) * (n - y)) % MOD;
}
}
cout<<ans;
return 0;
}
解释:对于代码中ans的解释
暴力对拍代码:(直接跑可能要3000s才能出答案)
#includeusing namespace std; typedef long long ll; const int MOD = 1e9 + 7; int main() { int n, k, ans = 0; cin >> n >> k; ///第一个点(sx, sy) 第二个点(tx, ty) for(int sx = 1; sx <= n; sx++) { for(int sy = 1; sy <= n; sy++) { for(int tx = 1; tx <= n; tx++) { for(int ty = 1; ty <= n; ty++) { if(sx == tx && sy == ty)continue; if((tx - sx) * (tx - sx) + (ty - sy) * (ty - sy) > k * k)continue; if(__gcd(abs(tx - sx), abs(ty - sy)) != 1)continue; ans++; } } } } cout< ; return 0; }2
答案:916585708
F:题目:
题解:直接用map或者set存即可,数据范围不大,不会mle或者tle。
坑点:要把a0=1提前存入,不然就会只有13/15分。(别问为啥知道,问就是白给)
代码:
#include
#include
#include
#include
#include
G:题目:
分析:一道稍微有点繁琐,题面有错的模拟。
输出的第一行,应该是被破坏的道路,房屋,田地的总数。(十分的蛋疼,比赛的时候完全按照题面只有2/20分)
注意:
①溅射伤害是高级炮弹击中的k*k区域的每一小块周围的8小块都会受到的伤害。
②该开long long的地方不要吝啬。
代码:(按照修改后的题意)
#include
#include
#include
#include
#include
H:题目:
分析:如果按位展开,每次都暴力计算判断是否乘除的话,必然拿不到满分(强数据会tle)。
所以在计算是否整除的时候做了以下优化:
①第一次计算总和时,借助了已经打好的按位取模后的乘权表
②之后双重for循环找交换的两位字母,在取模环境下,减去两个换前原字母所对应的值,加上两个换后字母对应的值进行O(1)的更新判断。
可行性分析:在无除法的运算过程中,加法和乘法的同余模定理确保了对每一步都取模后的结果不会让最后的答案不变。
代码:
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
ll f[2010];///f[i] = 26^i % M
int main(void)
{
string s;
cin >> s;
ll M;
cin >> M;
f[0] = 1 % M;
int n = s.size();
for (int i = 1; i <= n; i++)
f[i] = f[i - 1] * 26 % M;
ll sum = 0;
for (int i = 0; i < n; i++)
sum = (sum + f[n - 1 - i] * (s[i] - 'A')) % M;
if (sum == 0)
{
cout << "0 0" << endl;
return 0;
}
else
{
for (int i = 0; i < s.size(); i++)
{
for (int j = i + 1; j < s.size(); j++)
{
ll tmp = sum;
tmp = ((tmp - f[n - 1 - i] * (s[i] - 'A')) % M + M) % M;
tmp = ((tmp - f[n - 1 - j] * (s[j] - 'A')) % M + M) % M;
tmp = ((tmp + f[n - 1 - i] * (s[j] - 'A')) % M + M) % M;
tmp = ((tmp + f[n - 1 - j] * (s[i] - 'A')) % M + M) % M;
if (tmp == 0)
{
cout << i + 1 << " " << j + 1 << endl;
return 0;
}
}
}
}
cout << "-1 -1" << endl;
return 0;
}
注意:避免产生负数,取模之后的减法要加上模数,再取模确保计算结果为正。
I:题目:
分析:显然,这一题的数据不能一个点跑一次dijkstra。我们发现对于起点1到所有点的最短路,可以一次dijkstra完成。但如果此时,选择每一目的地出发,跑dijkstra,那需要再跑n-1次,显然不是明智的选择。
我们可以通过将边反存,这样所有从非起点指向1的边变成了1指向所有目的地。只要再dijkstra一次反向存边,便可计算出从目的地返回起点的最短路。
代码:
#include
#include
#include
#include
#include
#include
注意:不确定数值大小的话,都用long long(除了恶心的多校之外,一般不会卡ll);初始化的INF一定要大一些,如果使用0x3f3f3f3f会出错
J:题目:
分析:这是一题很棒的搜索题,题目中说确保每个点是至多是一个传送门的入口(仅仅只能说明传送门的出度是唯一的,即一个传送门对应一个目的地)
例如下图,
因此说明,传送门的传送位置是传送门;传送门死循环等状况也是可能的。
所以对于任意一点非障碍物a有以下情况:
(一)a是传送门
1:经过终点
2:传n次,落在合法位置
3:传n次,卡在障碍物
4:死循环
(二)a不是传送门
所以如果利用队列,我们需要将下一个即将压入队列的点进行预处理,才能当作正常bfs搜索操作。
难点处理:我们利用了map去映射传送门的起点对和终点对,写了函数Find_Next(a)去寻找点a进入传送门后的结果
1:正常情况:返回出口
2:卡在障碍物:返回-1,-1
3:死循环:返回-1,-1
4:只要经过终点:返回终点
代码:
#include
#include
#include
#include
#include
#include
Ps:题目数据似乎不强,没有涉及到传送门死循环的数据,但是处于严谨还是考虑上啦(毕竟补题)