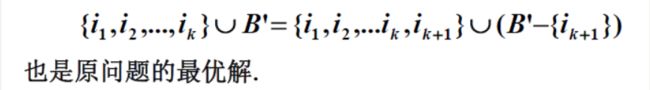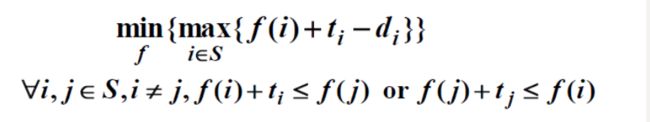贪心算法的正确性证明

贪心算法的正确性证明

摘要

贪心算法最难的部分就是正确性的证明，常用的方法有归纳法(对算法步数归纳、对问题归纳)和交换论证法（从最优解出发，不变坏地替换，得到贪心策略的解）。下面以三个例子说明这些正确性证法。

1. 活动选择问题——对算法步数归纳
2. 最优装载问题——对问题规模归纳
3. 最小延迟调度——交换论证

我的个人博客上的原文链接

活动选择问题

问题

$S=\{1,2,\dots ,n\}$为n项活动的集合，$s_i和f_i$分别为活动i的开始和结束时间，活动i与j相容当且仅当$s_i\ge f_j或s_j>=f_i$,求最大的活动集

贪心策略

按截止时间排序

伪代码：

正确性证明：对算法步数归纳

定理：算法Select执行到第k步，选择k项活动$i_1=1,i_2,\dots ,i_k$,那么存在最优解A包含$ i_1=1 ,i_2,…,i_k $

只要此定理成立，算法至多到第n步得到最优解

归纳基础：设$S=\{1,2,\dots .n\}$ 是活动集，活动按截止时间递增顺序排序，k=1，证明存在最优解包含活动1

任取最优解A，A中的活动按照截止时间递增的顺序排列，如果A的第一个活动为j，j不为1，令
$$A^{\prime }=(A-\{j\})\cup \{1\}$$
由于$f_1<=f_j，A^{\prime }$ 也是最优解，而且含有1

归纳步骤：

假设命题对k为真，证明对k+1也为真

算法执行到第k步，选择了活动$i_1=1,i_2,\dots ，i_k$ 根据归纳假设存在最优解A包含$i_1=1,i_2,\dots ,i_k$ ,设最优解A包含$i_1=1,i_2,…，i_k $ ,A中剩下的活动选自集合$S’= { i | i ∈ S , s_i \geq f_k } $ ,且$A=\{i_1,i_2,\dots ，i_k\}\cup B$ ,B一定是$S^{\prime }$ 的最优解

根据归纳基础，存在$S’ $ 的最优解B含有$S^{\prime }$ 中的第一个活动，设为$i_{k+1}$ ,且$|B’| = |B| $,于是

最优装载

问题

n个集装箱1,2…,n装上轮船，集装箱i的重量为$w_i$ ,轮船载重量限制为$c$ ,无体积限制。如何使装上船的集装箱最多。(假设每个集装箱重量小于c)

贪心策略

将集装箱按照从轻到重排序，轻者先装

正确性证明：对规模归纳

• 设箱子标号按照从轻到重记为1,2,…,n
• n = 1 贪心选择显然得到最优解
• 假设对规模n-1的输入得到最优解，证明对规模n的输入也得到最优解

最小延迟调度

问题

任务集合S，$\forall i∈S $ ,$d_i为截止时间,t_i为加工时间，均为正整数$

一个调度f:S→N,f(i)为任务i的开始时间。求最大延迟达到最小的调度，即求f 使得

贪心策略

按照截止时间$d_i$从小到大选择任务，安排时不留空闲时间

伪代码：

正确性证明：交换论证

上述算法的解的性质：没有空闲时间,没有逆序(不存在$f(i)<f(j),d_i>d_j$)

命题1：所有没有逆序、没有空闲时间的调度具有相同的最大延迟

命题1证明：$f_1和f_2$都没有逆序,具有相同截止时间的任务必须被连续安排。在这些连续安排的任务中最大延迟是最后一个任务，被延迟的时间只与已安排任务加工时间之和有关，与任务标号无关。

证明思想：从一个没有空闲时间的最优解出发，在不改变最优性的条件下，转变为没有逆序的解。

1. 如果一个最优调度存在逆序，那么存在i < n使得(i,i+1构成一个逆序)
2. 存在逆序(i,j),j = i + 1,那么交换i和j得到的解的逆序数减一，后面证明这个新的调度仍然最优
3. 至多经过n(n-1)/2次交换得到一个没有逆序的最优调度

交换相邻逆序任务(i,j)不影响最优性：

1. 交换i,j显然对其他任务的延迟时间没有影响
2. 交换后不增加j的延迟
3. 任务i在$f_2$的延迟$L_{2i}$ 小于任务j在$f_1 $ 的延迟$L_{1j}$ 因此小于$ f_1 $的最大延迟