Codeforces Round #612 (Div. 2)补题记录

Codeforces Round #612 (Div. 2)补题记录

A Angry Students

题目描述
It’s a walking tour day in SIS.Winter, so t groups of students are visiting Torzhok. Streets of Torzhok are so narrow that students have to go in a row one after another.

Initially, some students are angry. Let’s describe a group of students by a string of capital letters “A” and “P”:

“A” corresponds to an angry student
“P” corresponds to a patient student
Such string describes the row from the last to the first student.

Every minute every angry student throws a snowball at the next student. Formally, if an angry student corresponds to the character with index i in the string describing a group then they will throw a snowball at the student that corresponds to the character with index i+1 (students are given from the last to the first student). If the target student was not angry yet, they become angry. Even if the first (the rightmost in the string) student is angry, they don’t throw a snowball since there is no one in front of them.

Let’s look at the first example test. The row initially looks like this: PPAP. Then, after a minute the only single angry student will throw a snowball at the student in front of them, and they also become angry: PPAA. After that, no more students will become angry.
Your task is to help SIS.Winter teachers to determine the last moment a student becomes angry for every group.

Input
The first line contains a single integer t — the number of groups of students (1≤t≤100). The following 2t lines contain descriptions of groups of students.
The description of the group starts with an integer ki (1≤ki≤100) — the number of students in the group, followed by a string si, consisting of ki letters “A” and “P”, which describes the i-th group of students.

Output
For every group output single integer — the last moment a student becomes angry.

样例输入
3
12
APPAPPPAPPPP
3
AAP
3
PPA
样例输出
4
1
0

题目描述
A后面最大P的个数
思路
水

#pragma GCC optimize(3,"Ofast","inline")  	//G++
#include
 
#define TEST freopen("C:\\Users\\hp\\Desktop\\ACM\\in.txt","r",stdin);
#define mem(a,x) memset(a,x,sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
 
using namespace std;
typedef long long ll;
 
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
const int maxn = 1e6+5;
char s[maxn];
int main()
{
    ios;
    int T;
    cin>>T;
    while(T--)
    {
        int flag=1,ans=0,sum=0;
        int n;
        cin>>n;
        cin>>s+1;
        int len=strlen(s+1);
        for(int i=1;i<=len;i++)
        {
            if(s[i]=='P'&&flag)
                continue;
            else
                flag=0;
            if(s[i]=='A')
            {
                ans=max(ans,sum);
                sum=0;
            }
            else
            {
                sum++;
            }
        }
        ans=max(ans,sum);
        cout<<ans<<"\n";
 
    }
}

B. Hyperset

题目描述
Bees Alice and Alesya gave beekeeper Polina famous card game “Set” as a Christmas present. The deck consists of cards that vary in four features across three options for each kind of feature: number of shapes, shape, shading, and color. In this game, some combinations of three cards are said to make up a set. For every feature — color, number, shape, and shading — the three cards must display that feature as either all the same, or pairwise different. The picture below shows how sets look.

Polina came up with a new game called “Hyperset”. In her game, there are n cards with k features, each feature has three possible values: “S”, “E”, or “T”. The original “Set” game can be viewed as “Hyperset” with k=4.
Similarly to the original game, three cards form a set, if all features are the same for all cards or are pairwise different. The goal of the game is to compute the number of ways to choose three cards that form a set.
Unfortunately, winter holidays have come to an end, and it’s time for Polina to go to school. Help Polina find the number of sets among the cards lying on the table.
Input
The first line of each test contains two integers n and k (1≤n≤1500, 1≤k≤30) — number of cards and number of features.
Each of the following n lines contains a card description: a string consisting of k letters “S”, “E”, “T”. The i-th character of this string decribes the i-th feature of that card. All cards are distinct.

Output
Output a single integer — the number of ways to choose three cards that form a set.

样例输入
5 4
SETT
TEST
EEET
ESTE
STES
样例输出
2

翻译成中文
定义一个集合的包含3个串，且对于这3个串的每一列都是相同或者都为不同的，比如SET,EST那么对于第3个串只能是TTT,求n个串中最多能构成多少个集合
思路
枚举任意两个字符串推断出第3个字符串询问该字符串是否存在

 #pragma GCC optimize(3,"Ofast","inline")  	//G++
#include
 
#define TEST freopen("C:\\Users\\hp\\Desktop\\ACM\\in.txt","r",stdin);
#define mem(a,x) memset(a,x,sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
 
using namespace std;
typedef long long ll;
 
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
const int maxn = 1e6+5;
string fin(string a,string b)
{
    string ans;
    for(int i=0;i<a.size();i++)
    {
        if(a[i]==b[i])
        {
//            if(a[i]=='S')
//                ans+="S";
//            else if(a[i]=='E')
//                ans+="E";
//            else
//                ans+="T";				//string+=常量 快于 +=变量
            ans+=a[i];
        }
        else if(a[i]=='S'&&b[i]=='E'||b[i]=='S'&&a[i]=='E')
            ans+="T";
        else if(a[i]=='E'&&b[i]=='T'||b[i]=='E'&&a[i]=='T')
            ans+="S";
        else
            ans+="E";
    }
    return ans;
}
string s[maxn];
unordered_map<string,vector<int> >mp;
int main()
{
    ios;
    int ans=0;
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        cin>>s[i];
        mp[s[i]].push_back(i);
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;j<=n;j++)
        {
            string tmp=fin(s[i],s[j]);
            if(mp[tmp].size()==0) continue;
            int pos=lower_bound(mp[tmp].begin(),mp[tmp].end(),j)-mp[tmp].begin();
            ans+=mp[tmp].size()-pos;
        }
    }
    cout<<ans<<"\n";
}

写的麻烦了，但也能过，可以直接ans+=mp[tmp]，最后结果除3即可。

string+=常量 快于 +=变量

C. Garland

Vadim loves decorating the Christmas tree, so he got a beautiful garland as a present. It consists of n light bulbs in a single row. Each bulb has a number from 1 to n (in arbitrary order), such that all the numbers are distinct. While Vadim was solving problems, his home Carp removed some light bulbs from the garland. Now Vadim wants to put them back on.

Vadim wants to put all bulb back on the garland. Vadim defines complexity of a garland to be the number of pairs of adjacent bulbs with numbers with different parity (remainder of the division by 2). For example, the complexity of 1 4 2 3 5 is 2 and the complexity of 1 3 5 7 6 4 2 is 1.

No one likes complexity, so Vadim wants to minimize the number of such pairs. Find the way to put all bulbs back on the garland, such that the complexity is as small as possible.

Input
The first line contains a single integer n (1≤n≤100) — the number of light bulbs on the garland.
The second line contains n integers p1, p2, …, pn (0≤pi≤n) — the number on the i-th bulb, or 0 if it was removed.

Output
Output a single number — the minimum complexity of the garland.

样例输入
5
0 5 0 2 3
样例输出
2

题目描述
1-n，n个数字排列，0为未添置数需要将剩余数字置入进去，保证价值最小，价值的定义为：相邻两位奇偶性不同则价值加1。
思路
贪心做法，dp也可以做
针对连续的0分3种情况
1.左右端都存在数字，且都为奇数或偶数。这样我们可以都填奇数或偶数，如果填不了的话随便填贡献+2
2.左端或右端存在数字，即在开头或者结尾。这样我们可以填与该数字奇偶性一致的数字，如果填不了随便填贡献+1
3左端右端都存在数字，且奇偶性不同，这样我们只能随便填，贡献值必+1
按照区间大小，从小到大贪心。优先贪心方案1，之后在贪心方案2.方案3ans必+1

#pragma GCC optimize(3,"Ofast","inline")  	//G++
#include
 
#define TEST freopen("C:\\Users\\hp\\Desktop\\ACM\\in.txt","r",stdin);
#define mem(a,x) memset(a,x,sizeof(a))
#define debug(x) cout << #x << ": " << x << endl;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
 
using namespace std;
typedef long long ll;
 
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
const int maxn = 1e6+5;
 
int a[maxn];
vector<pair<int,int> >p;
int n,ji,ou,ans=0;
int check(int x,int y)
{
    if(x==-1)
        return (y&1)+2;//端点数且为奇 返回3
    if(y==-2)
        return (x&1)+2;//端点数且为偶 返回4
    x&=1,y&=1;
    if(x==y) //非端点数且两端同奇偶数性 奇数返回1 偶数返回0
    {
        return x;
    }
    else//两端奇偶性不同返回-1
        return -1;
}
void init()
{
    cin>>n;
    ou=n/2,ji=ou+(n&1);
    for(int i=1; i<=n; i++)
    {
        cin>>a[i];
        if(a[i]==0) continue;
        if(a[i]&1) ji--;
        else ou--;
    }
    //统计剩余奇数 偶数的个数
}
void solve()
{
    int last,tmp=0;
    a[0]=-1;
    a[n+1]=-2;
    for(int i=1; i<=n+1; i++)
    {
        if(a[i]==0&&a[i-1]!=0)
            last=i;
        if(a[i]==0)
            tmp++;
        if(a[i]!=0&&a[i-1]==0)
        {
            int now=check(a[last-1],a[i]);
            if(now==-1)
            {
                ans++;
            }
            else
 
                p.push_back(make_pair((now<=1)?i-last:i-last+200,now));
 
            tmp=0;
        }
    }
    sort(p.begin(),p.end());
    for(int i=0; i<p.size(); i++)
    {
        int tmp=p[i].second;
        if(tmp==1)
        {
            if(ji>=p[i].first)
                ji-=p[i].first;
            else
                ans+=2;
        }
        else if(tmp==0)
        {
            if(ou>=p[i].first)
                ou-=p[i].first;
            else
                ans+=2;
        }
        else if(tmp==3)
        {
            if(ji>=p[i].first-200)
                ji-=p[i].first-200;
            else
            {
                ans+=1;
            }
        }
        else
        {
            if(ou>=p[i].first-200)
                ou-=p[i].first-200;
            else
                ans+=1;
        }
    }
}
int solve2()
{
    int ans=0;
    for(int i=2;i<=n;i++)
    {
        if(a[i-1]!=0&&a[i]!=0&&check(a[i-1],a[i])==-1)
        {
            ans++;
        }
    }
    return ans;
}
int main()
{
    ios
    init();
    if(n==1)
    {
        cout<<"0\n";
        return 0;
    }
    solve();
    ans+=solve2();
    cout<<ans<<"\n";
}

D. Numbers on Tree

题目描述
Evlampiy was gifted a rooted tree. The vertices of the tree are numbered from 1 to n. Each of its vertices also has an integer ai written on it. For each vertex i, Evlampiy calculated ci — the number of vertices j in the subtree of vertex i, such that aj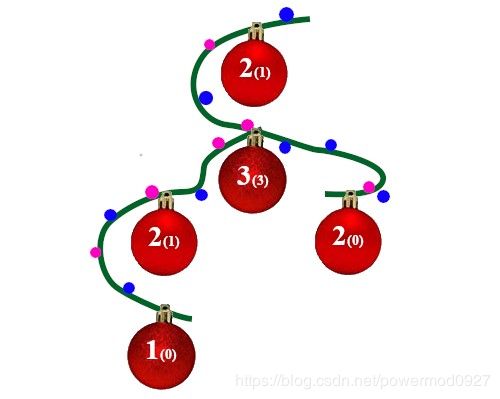
Illustration for the second example, the first integer is ai and the integer in parentheses is ci
After the new year, Evlampiy could not remember what his gift was! He remembers the tree and the values of ci, but he completely forgot which integers ai were written on the vertices.

Help him to restore initial integers!

Input
The first line contains an integer n (1≤n≤2000) — the number of vertices in the tree.

The next n lines contain descriptions of vertices: the i-th line contains two integers pi and ci (0≤pi≤n; 0≤ci≤n−1), where pi is the parent of vertex i or 0 if vertex i is root, and ci is the number of vertices j in the subtree of vertex i, such that aj

It is guaranteed that the values of pi describe a rooted tree with n vertices.

Output
If a solution exists, in the first line print “YES”, and in the second line output n integers ai (1≤ai≤109). If there are several solutions, output any of them. One can prove that if there is a solution, then there is also a solution in which all ai are between 1 and 109.

If there are no solutions, print “NO”.

样例输入
5
0 1
1 3
2 1
3 0
2 0
样例输出
YES
2 3 2 1 2

翻译成中文
给出一棵有根树，每个节点都有一个权值，代表的是在其子树中有多少个节点的val比他小，现在要求根据每个点的权值构造出1~n的val数列
思路
首先证明：n个节点一定可以用1-n的数字去放。因为1-n的数字都是不同的，那么不会有相对大小的问题，不会有节点之间相互影响而导致答案错误。放相同值的节点也就是少一个差值，我们完全可以用放的方式去避免，比如小的放在大的上面。
其次证明：如果节点的C值小于节点的size，那么一定存在这种方案。
我们从顶点开始放，因为我们放1到n的数字，那么有多少个数字没放是一定的，所以我们相当于是从没放的数字当中找第C+1大的数字放上去，然后标记放的数字，向下递归。一定满足。

#pragma GCC optimize(3,"Ofast","inline")  	//G++
#include
 
#define TEST freopen("C:\\Users\\hp\\Desktop\\ACM\\in.txt","r",stdin);
#define mem(a,x) memset(a,x,sizeof(a))
#define debug(x) cout << #x << ": " << x << endl;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
 
using namespace std;
typedef long long ll;
 
const int inf=0x3f3f3f3f;
const int mod=1e9+7;
const int maxn = 1e6+5;
 
 
int n;
vector<int>edge[maxn];
int ans[maxn],c[maxn],vis[maxn],siz[maxn];
void dfs(int u)
{
    siz[u]=1;
    int sum=0,k;
    for(int i=1;i<=n;i++)
    {
        if(!vis[i])
            sum++;
        if(sum==c[u]+1)
        {
            k=i;
            break;
        }
    }
    ans[u]=k;
    vis[k]=1;
    for(auto to:edge[u])
    {
        int v=to;
        dfs(v);
        siz[u]+=siz[v];
    }
    if(c[u]>siz[u]-1)
    {
        cout<<"NO\n";
        exit(0);
    }
}
int main()
{
    int root=0;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int fa;
        cin>>fa>>c[i];
        if(fa==0)
            root=i;
        else
            edge[fa].push_back(i);
    }
    dfs(root);
    cout<<"YES\n";
    for(int i=1;i<=n;i++)
    {
        cout<<ans[i]<<" ";
    }
    cout<<"\n";
}

exit(0);可以直接退出递归结束程序

E,F待补