算法模型---逻辑回归学习

逻辑回归的特点

逻辑回归的用途

第一用来预测，第二寻找因变量的影响因素。

逻辑回归的适用范围

数据类型

自变量可以是离散值，也可以是连续值;
因变量是二分类变量，也可以是多分类；(多分类使用softmax函数而不是sigmoid函数)
逻辑回归中的离散变量
数据不平衡问题：
训练结果会偏袒大类:
来源：Logistic回归的非平衡数据问题及其解决方法
Logistic模型对非平衡数据的敏感性：测度、修正与比较
小类配平和大类配平

逻辑回归的优点

原理的相对简单，可解释性强等优点,它还可以作为众多集成算法以及深度学习的基本组成单位
Logistic回归分析报告结果解读分析

逻辑回归的局限性

逻辑回归模型的引入(从线性回归到Logistic回归)

广义线性模型
这一家族中模型的形式基本一致，不同的是因变量不同

• 如果是连续的，就是线性回归
• 如果是二项分布，就是logistic回归
• 如果是poisson分布，就是poisson回归
• 如果负二项分布，就是负二项回归

线性回归和Logistic回归都是广义线性模型的特例。
假设有一个因变量$y$和一组自变量$x_1,x_2,x_3,...,x_n$，其中$y$为连续变量，我们可以拟合一个线性方程：
$$y=w_0+w_1\ast x_1+w_2\ast x_2+w_3\ast x_3+\cdots +w_n\ast x_n-----(1)$$
并通过最小二乘法估计各个$w$系数的值。
如果$y$为二分类变量，只能取值0或1，那么线性回归方程就会遇到困难: 方程右侧是一个连续的值，取值为负无穷到正无穷，而左侧只能取值[0,1]，无法对应。为了继续使用线性回归的思想，统计学家想到了一个变换方法，就是将方程右边的取值变换为[0,1]。最后选中了sigmoid函数：$s(x)=\frac{1}{1+e^{-x}}$，sigmoid函数曲线如下：

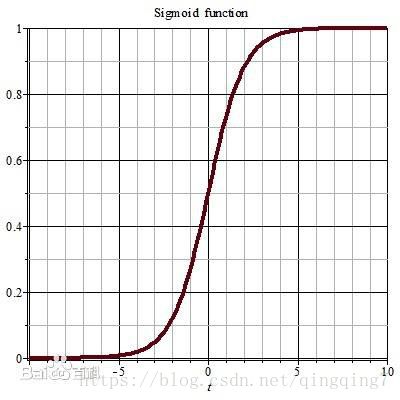
Sigmoid函数在两侧能很快收敛至0和1，此特性很适合逻辑回归的需要，将方程(1)右侧代入sigmoid函数有

$$y=\frac{1}{1+e^{-(w_0+w_1\ast x_1+w_2\ast x_2+w_3\ast x_3+...+w_n\ast x_n)}}----(2)$$
按照(2)式，对于任意取值的x,因变量y的取值范围都为(0~1)；但是在分类模型中，y的取值只能是1或0；如果令$y=p$，我们还需要做一些规定，比如当$p\ge 0.5$时，y的取值为1；当$p<0.5$时,y的取值为0；当我们通过一定的方法，得到一组合适的参数$w_0、w_1、w_2、w_3、...、w_n$,那么只要样本代入(2)式，根据计算出来p值的大小就可以对的样本的类别进行判定；此时结果p就相当于y取1的概率，与此对应的，y取0的概率为$1-p$。sigmoid函数好处在于在x=0的两侧能很快收敛至0和1，保证能够匹配大部分样本的类别。
那么如何来求解这样一组参数呢？
参数的最优解应该要满足这样的要求：最优参数应该让尽可能多的样本在给定的属性值下其类别尽可能呈现其本来的样子；也就是对于全体样本，在给定的属性值和类别取值下，通过(2)式计算得到的类别取值的联合概率应该最大。
这里我们就引出了逻辑回归模型参数求解的目标函数。

补充知识：

优势$\Omega$
优势，是事件发生与不发生概率之比，用符号$\Omega$来表示。
$$\Omega =\frac{p}{1-p}=e^{(w_0+w_1\ast x_1+w_2\ast x_2+w_3\ast x_3+...+w_n\ast x_n)}$$
$\Omega$是$p$的单调函数，保证了$\Omega$和p增长的一致性，$\Omega$的取舍范围是$(0,+\infty )$；
如果再对$\Omega$取对数，则有
$$ln\Omega =ln\frac{p}{1-p}=w_0+w_1\ast x_1+w_2\ast x_2+w_3\ast x_3+...+w_n\ast x_n$$
$logit$变换
上述两步变换称为$logit$变换，$ln\Omega$称为$logitP$，$logitP$的取舍范围$(-\infty ,+\infty )$，与一般线性回归模型吻合，同时与p之间保值单调一致性。这样我们完成了从一般线性回归到逻辑回归的转换。
$logit$变换在后面的参数求解中还会用到，可以简化推导过程。

逻辑回归模型的参数估计

设$y$是0-1型变量，$(x_1,x_2,\dots ,x_p)$是与$y$相关的确定性变量即特征变量；n组观测数据，记为$(x_{i1},x_{i2},\dots ,x_{ip};y_i)(i=1,2,\dots ,n)$,其中$y_i$是取值为0或1的随机变量。
$y_i$是均值为$p_i$的0-1分布，概率函数为$P(y_i=1)=p_i$；$P(y_i=0)=1-p_i$，我们可以将概率函数合写为$P(y_i)=p_i^{y_i}(1-p_i{)}^{1-y_i};i=1,2,\dots ,n;y_i=0,1$；于是$(y_1,y_2,\dots ,y_n)$的似然函数可以写作
$$L=\prod _{i=1}^{n}p(y_i)=\prod _{i=1}^n{p}_i^{y_i}(1-p_i{)}^{1-y_i}----(3)$$
(3)式中$p_i=\frac{1}{1+e^{-(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}}$,我们的目标就是求取一组参数$w_0、w_1、\dots 、w_p$，使的似然函数L最大。
为了计算方便，对$L$取对数(为什么要取对数呢？因为取对数后，乘法就变成了加法，后面利用梯度下降法时可更好的求偏导，且未改变原似然函数的单调性，如果lnL取到最大值则L也能取到最大值。)
$$\begin{array}{ccc}lnL& =& ln({\prod }_{i=1}^n{p}_i^{y_i}(1-p_i{)}^{1-y_i})\\ & =& ln({\prod }_{i=1}^n{p}_i^{y_i})+ln({\prod }_{i=1}^n(1-p_i{)}^{1-y_i})\\ & =& {\sum }_{i=1}^n{y}_{i}ln{p}_i+{\sum }_{i=1}^n(1-y_i)ln(1-p_i)\\ & =& {\sum }_{i=1}^{n}ln(1-p_i)+{\sum }_{i=1}^n{y}_{i}ln\frac{p_i}{1-p_i}\end{array}$$
将$p_i=\frac{1}{1+e^{-(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}}$及$ln\Omega =ln\frac{p}{1-p}=w_0+w_1\ast x_1+w_2\ast x_2+w_3\ast x_3+...+w_n\ast x_n$代入到上式，可以得到
$$\begin{array}{ccc}lnL& =& -{\sum }_{i=1}^{n}ln(1+e^{(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})})+{\sum }_{i=1}^n{y}_i(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})\\ & =& {\sum }_{i=1}^n\left[y_i(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})-ln(1+e^{(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})})\right]\end{array}$$
令$w=(w_0,w_1,\dots ,w_p{)}^T,x_i=(1,x_{i1},\dots ,x_{ip}{)}^T,x_i中添加了1是为了与w相匹配$。
则$lnL$可写成如下形式：
$$\begin{array}{ccc}lnL& =& {\sum }_{i=1}^n\left[y_i(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})-ln(1+e^{(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})})\right]\\ & =& {\sum }_{i=1}^n\left[y_i{w}^T{x}_i-ln(1+e^{w^T{x}_i})\right]\end{array}$$
如何选取一组参数$w_0、w_1、\dots 、w_p$使得上式最大，这是一个最优化问题。考虑到参数数量的不确定，即参数数量很大，此时直接求解方程组的解变的很困难，或者根本就求不出精确的参数。于是，可以采用梯度下降法和牛顿法等最优化算法。

使用梯度上升法(梯度下降法)求解逻辑回归模型的参数

$lnL$取到最大值，即$J(w)=-lnL(w)$取到最小值.
如果采用梯度下降法求最小值，则$\beta$的更新过程应当如下：
$$w=w-\alpha \frac{\partial J(w)}{\partial w}=w-\alpha \frac{\partial (-lnL(w))}{\partial w}$$
下面计算梯度部分。
$$\begin{array}{ccc}\frac{\partial (-lnL(w))}{\partial w}& =& \frac{\partial (-{\sum }_{i=1}^n\left[y_i{w}^T{x}_i-ln(1+e^{w^T{x}_i})\right])}{\partial w}\\ & =& \frac{\partial ({\sum }_{i=1}^n\left[ln(1+e^{w^T{x}_i})-y_i{w}^T{x}_i\right])}{\partial w}\\ & =& {\sum }_{i=1}^n(\frac{e^{w^T{x}_i}}{1+e^{w^T{x}_i}}-y_i)\frac{\partial (w^T{x}_i)}{\partial w}\\ & =& {\sum }_{i=1}^n(\frac{1}{1+e^{-w^T{x}_i}}-y_i)\frac{\partial (w^T{x}_i)}{\partial w}\\ & =& {\sum }_{i=1}^n(\frac{1}{1+e^{-w^T{x}_i}}-y_i)\frac{\partial (w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}{\partial w}\end{array}$$
不防令$\frac{1}{1+e^{-w^T{x}_i}}-y_i=e_i$,注意看，其实$e_i$正好就是样本i的预测误差)则上式可化简为
$$\begin{array}{ccc}\frac{\partial (-lnL(w))}{\partial w}& =& {\sum }_{i=1}^n{e}_i\frac{\partial (w^T{x}_i)}{\partial w}\\ & =& {\sum }_{i=1}^n{e}_i\frac{\partial (w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}{\partial w}\end{array}$$
先计算$\frac{\partial (-lnL(w))}{\partial w}$各分量
$$\begin{array}{ccccc}\frac{\partial (-lnL(w))}{\partial w_0}& =& {\sum }_{i=1}^n{e}_i\frac{\partial (w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}{\partial w_0}& =& {\sum }_{i=1}^n{e}_i\ast 1\\ \frac{\partial (-lnL(w))}{\partial w_1}& =& {\sum }_{i=1}^n{e}_i\frac{\partial (w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}{\partial w_1}& =& {\sum }_{i=1}^n{e}_i\ast x_{i1}\\ \cdots & =& \cdots & =& \cdots \\ \frac{\partial (-lnL(w))}{\partial w_p}& =& {\sum }_{i=1}^n{e}_i\frac{\partial (w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}{\partial w_p}& =& {\sum }_{i=1}^n{e}_i\ast x_{ip}\end{array}$$
故$\frac{\partial (-lnL(w))}{\partial w}$可写成
$$\begin{array}{ccc}\frac{\partial (-lnL(w))}{\partial w}& =& \left[\begin{array}{c}{\sum }_{i=1}^n{e}_i\ast 1\\ {\sum }_{i=1}^n{e}_i\ast x_{i1}\\ \cdots \\ {\sum }_{i=1}^n{e}_i\ast x_{ip}\end{array}\right]\\ & =& \left[\begin{array}{c}{e}_1+e_x+\cdots +e_n\\ e_1{x}_{11}+e_2{x}_{21}+\cdots +e_n{x}_{n1}\\ \cdots \\ e_1{x}_{1p}+e_2{x}_{2p}+\cdots +e_n{x}_{np}\end{array}\right]\\ & =& {\left[\begin{array}{c}1+x_{11}+x_{12}+\cdots +x_{1p}\\ 1+x_{21}+x_{22}+\cdots +x_{2p}\\ \cdots \\ 1+x_{n1}+x_{n2}+\cdots +x_{np}\end{array}\right]}^T\ast \left[\begin{array}{c}{e}_1\\ \cdots \\ e_n\end{array}\right]\end{array}$$
记
$$\left[\begin{array}{c}1,x_{11},x_{12},\cdots ,x_{1p}\\ 1,x_{21},x_{22},\cdots ,x_{2p}\\ \cdots \\ 1,x_{n1},x_{n2},\cdots ,x_{np}\end{array}\right]=X$$
$$\left[\begin{array}{c}{e}_1\\ \cdots \\ e_n\end{array}\right]=E$$
则
$$\frac{\partial (-lnL(w))}{\partial w}=X^{T}E$$
实际上的计算应该不需要这么麻烦，但大学时学的偏微分和矩阵运算都忘光了。就采用这种笨一点的方法
则参数更新公式可写成
$$w=w-\alpha X^{T}E$$
到此我们就将梯度下降法求解最优参数的更新公式推导出来了。初始化的时候，我们可以先令所有参数都为1，然后逐步迭代优化。迭代足够的次数或者前后再次更新变化很小，就可以停止迭代。

分界面的求解

通过定一个阈值，比如$p_0=0.5$，然后$p\ge p_0$是一类，则$p<p_0$是另一类；
即$p_i=\frac{1}{1+e^{-(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}}\ge 0.5$是一类，$p_i=\frac{1}{1+e^{-(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}}<0.5$是另一类；
或者换一种表达
$w_0+w_1{x}_{i}1+\cdots +w_p{x}_{i}p>0$是一类，$w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip}<0$是另一类；在原数据空间，$w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip}$就是分界面。

类别预测

将测试数据代入方程
$p_i=\frac{1}{1+e^{-(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}}$，并确定一个阈值，如果定阈值为0.5，则在二分类模型中，$p_i>0.5$即为1，小于0.5即为0

逻辑回归用于多分类

来源：https://blog.csdn.net/szu_hadooper/article/details/78619001
普通的logistic回归只能针对二分类(Binary Classification)问题，要想实现多个类别的分类，我们必须要改进logistic回归，让其适应多分类问题。
关于这种改进，有两种方式可以做到。

第一种方式

是直接根据每个类别，都建立一个二分类器，带有这个类别的样本标记为1，带有其他类别的样本标记为0。假如我们有个类别，最后我们就得到了个针对不同标记的普通的logistic分类器。
假如给定数据集$X\in R^{m\times n}$，它们的标记$Y\in R^k$，即这些样本有个不同的类别。

我们挑选出标记为$c(c\le k)$的样本，将挑选出来的带有标记的样本的标记置为1，将剩下的不带有标记的样本的标记置为0。然后就用这些数据训练出一个分类器，我们得到$h_c(x)$(表示针对标记的logistic分类函数)。

按照上面的步骤，我们可以得到k个不同的分类器。针对一个测试样本，我们需要找到这个分类函数输出值最大的那一个，即为测试样本的标记：
$$argma{x}_c{h}_c(x),c=1,2,\cdots ,k$$

第二种方式

是修改logistic回归的损失函数，让其适应多分类问题。这个损失函数不再笼统地只考虑二分类非1就0的损失，而是具体考虑每个样本标记的损失。这种方法叫做softmax回归，即logistic回归的多分类版本。
参考：Softmax函数与交叉熵

Softmax函数

在Logistic regression二分类问题中，我们可以使用sigmoid函数将输入$Wx+b$映射到(0,1)区间中，从而得到属于某个类别的概率。将这个问题进行泛化，推广到多分类问题中，我们可以使用softmax函数，对输出的值归一化为概率值。
这里假设在进入softmax函数之前，已经有模型输出C值，其中C是要预测的类别数，模型可以是全连接网络的输出a，其输出个数为C，即输出为$a_1,a_2,...,a_C$。
所以对每个样本，它属于类别$i$的概率为：
$$y_i=\frac{e^{a_i}}{{\sum }_{k=1}^C{e}^{a_k}}{\forall }_i\in 1...C$$
通过上式可以保证${\sum }_{i=1}^C{y}_i=1$，即属于各个类别的概率和为1。
Softmax函数求导

softmax 回归

损失函数：对数似然函数
机器学习里面，对模型的训练都是对Loss function进行优化，在分类问题中，我们一般使用最大似然估计(Maximum likelihood estimation)来构造损失函数。对于输入的$x$，其对应的类标签为$t$，我们的目标是找到这样的$\theta$使得$p(t|x)$最大。在二分类的问题中，我们有：
$p(t|x)=(y{)}^t(1-y{)}^{1-t}$
其中，$y=f(x)$是模型预测的概率值，$t$是样本对应的类标签。
将问题泛化为更一般的情况，多分类问题：
$$p(t|x)=\prod _{i=1}^{C}P(t_i|x{)}^{t_i}=\prod _{i=1}^C{y}_i^{t_i}$$
其中$t_i$是样本m属于类别i的概率，$y_i$是模型对样本m预测为属于类别i的概率。
由于连乘可能导致最终结果接近0的问题，一般对似然函数取对数的负数，变成最小化对数似然函数。
$$l_{CE}=-logp(t|x)=-log\prod _{i=1}^C{y}_i^{t_i}=-\sum _{i=i}^C{t}_{i}log(y_i)$$
损失函数求导
对单个样本来说，loss function $l_{CE}$对输入$a_j$的导数为：
$$\frac{\partial l_{CE}}{{\partial }_{a_j}}=-\sum _{i=1}^C\frac{\partial t_{i}log(y_i)}{\partial a_j}=-\sum _{i=1}^C{t}_i\frac{\partial log(y_i)}{\partial a_j}=-\sum _{i=1}^C{t}_i\frac{1}{y_i}\frac{\partial y_i}{\partial a_j}$$
上面对$\frac{\partial y_i}{\partial a_j}$求导结果已经算出：
当$i=j$时：$\frac{\partial y_i}{\partial a_j}=y_i(1-y_j)$
当$i̸=j$时：$\frac{\partial y_i}{\partial a_j}=-y_i{y}_j$

所以，将求导结果代入上式：
$$\begin{array}{ccc}-{\sum }_{i=1}^C{t}_i\frac{1}{y_i}\frac{\partial y_i}{\partial a_j}& =& -\frac{t_i}{y_i}\frac{\partial y_i}{\partial a_j}-{\sum }_{i̸=j}^C\frac{t_i}{y_i}\frac{\partial y_i}{\partial a_j}\\ & =& -\frac{t_j}{y_i}{y}_i(1-y_j)-{\sum }_{i̸=j}^C\frac{t_i}{y_i}(-y_i{y}_j)\\ & =& -t_j+t_j{y}_j+{\sum }_{i̸=j}^C{t}_i{y}_j\\ & =& -t_j+{\sum }_{i=1}^C{t}_i{y}_j\\ & =& -t_j+y_j{\sum }_{i=1}^C{t}_i\\ & =& -t_j+y_j\end{array}$$
这个就量参数的更新公式，其实与BPNN中的是一样的。

也可参考：Deep Learning 学习随记(三)Softmax regression

逻辑回归用于回归模型

逻辑回归主要用于分类，稍加改造也可以用于回归模型，但只适用于极特殊的分布函数，感觉没什么应用价值。
但可以从下面的角度来应用：
正如在前面在类别判断中计算取1的概率一样 $p_i=\frac{1}{1+e^{-(w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip})}}$ ，这个函数是非线性的，越靠近1相互之间越难以区分。如果直接用上式作回归结果，在类似于信用评分这样的场景就不好用。但$w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip}$却是线性的，个人以为可以利用逻辑回归获得各变量的权重，而$w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip}$就是相应的综合评分。为了将评分结果约束到一定范围，可以在建模型之前对变量取值进行类似归一化的处理再建模；也可以先建模，再利用$w_0+w_1{x}_{i1}+\cdots +w_p{x}_{ip}$对历史数据预测结果来进行约束，比如除以历史预测结果的最大值，这样就将结果约束到[-1,1]之间，但是我们知道，这样的话可能会出现新的预测结果大于1或小于-1的情况。如果大于1，说明是极好的，不防就令所有大于1的结果为1.这样整个下来就相当于一个线性预测的效果。

逻辑回归模型的检验(及自变量的选择)

逻辑回归方程的显著性检验的目的是检验所有自变量与logitP的线性关系是否显著，是否可以选择线性模型。原假设是假设各回归系数同时为0，自变量全体与logitP的线性关系不显著。如果方程中的诸多自变量对logitP

的线性解释有显著意义，那么必然会使回归方程对样本的拟合得到显著提高。可通过对数似然比测度拟合程度是否有所提高。

我们通常采用似然比检验统计量 $-ln(\frac{L}{L_{x_i}}{)}^2$
也可称为似然比卡方,其中$L$表示引入变量 $x_i$前回归方程的似然函数值，$L_{x_i}$表示引入变量 $x_i$后回归方程的似然函数值。似然比检验统计量越大表明引入变量 $x_i$越有意义。如果似然比卡方观测值的概率$p$值小于给定的显著性水平，不接受原假设，即认为自变量全体与$logitP$之间的线性关系显著。反之，线性关系不显著。
另外可参考：
怎样用SPSS做二项Logistic回归分析？结果如何解释？

Wald检验：
似然比检验
比分检验
spss二分类的logistic回归的操作和分析方法
利用R语言+逻辑回归实现自动化运营

回归系数的显著性检验

逻辑回归系数的显著性检验是检验方程中各变量与$logitP$之间是否具有线性关系。原假设是假设变量$x_i$与$logitP$之间的线性关系不显著，即$w_i=0$。

逻辑回归模型的评估方法

来源：2016年07月14日 18:09:35

正确率
TP、FP、FN、TN

• 误检率： fp rate = sum(fp) / (sum(fp) + sum(tn))
• 查准率： precision rate = sum(tp) / (sum(tp) + sum(fp))
• 查全率： recall rate = sum(tp) / (sum(tp) + sum(fn))
• 漏检率：miss rate = sum(fn) / (sum(tp) + sum(fn))

ROC曲线、AUC
ROC曲线的横坐标为false positive rate(FPR)，纵坐标为 true positive rate(TPR)
Kappa statics
Kappa值，即内部一致性系数(inter-rater,coefficient of internal consistency)，是作为评价判断的一致性程度的重要指标。取值在0～1之间。Kappa≥0.75两者一致性较好；0.75>Kappa≥0.4两者一致性一般；Kappa<0.4两者一致性较差。
第一个图上，所显示的Kappa值有0.9356，那就算很好了。
Mean absolute error 和 Root mean squared error
平均绝对误差和均方根误差，用来衡量分类器预测值和实际结果的差异，越小越好。

Relative absolute error 和 Root relative squared error
相对绝对误差和相对均方根误差，有时绝对误差不能体现误差的真实大小，而相对误差通过体现误差占真值的比重来反映误差大小。

逻辑回归的正则化

当模型的参数过多时，很容易遇到过拟合的问题。而正则化是结构风险最小化的一种实现方式，通过在经验风险上加一个正则化项，来惩罚过大的参数来防止过拟合。

• 正则化是符合奥卡姆剃刀(Occam’s razor)原理 的：在所有可能选择的模型中，能够很好地解释已知数据并且十分简单的才是最好的模型。

我们来看一下underfitting，fitting跟overfitting的情况：

显然，最右这张图overfitting了，原因可能是能影响结果的参数太多了。典型的做法在优化目标中加入正则项，通过惩罚过大的参数来防止过拟合：
$$J(w)=>J(w)+\lambda ||w|{|}_p$$
p=1或者2，表示L1 范数和 L2范数，这两者还是有不同效果的。

L1范数： 是指向量中各个元素绝对值之和，也有个美称叫“稀疏规则算子”(Lasso regularization)。那么，参数稀疏 有什么好处呢？

一个关键原因在于它能实现 特征的自动选择。一般来说，大部分特征 $x_i$和输出 $y_i $之间并没有多大关系。在最小化目标函数的时候考虑到这些额外的特征 $x_i$，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的信息反而会干扰了对正确 $y_i$ 的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为0。

L2范数： 它有两个美称，在回归里面，有人把有它的回归叫“岭回归”(Ridge Regression)重点内容，有人也叫它“权值衰减”(weight decay)。

它的强大之处就是它能 解决过拟合 问题。我们让 L2 范数的规则项$ ||w||_2$ 最小，可以使得 w 的每个元素都很小，都接近于0，但与 L1范数不同，它不会让它等于0，而是接近于0，这里还是有很大区别的。而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。咦，你为啥说越小的参数表示的模型越简单呢？ 其实我也不知道，我也是猜，可能是因为参数小，对结果的影响就小了吧。

为了更直观看出两者的区别，我再放一张图：

为了简单，上图只考虑了w为二维($w^1$,$w^2$)的情况。彩色等高线是($w^1$,$w^2$)；而左边黑色矩形 $||w||_1$和右边的圆形$ ||w||_2

• 一句话总结就是：L1 会趋向于产生少量的特征，而其他的特征都是0，而 L2 会选择更多的特征，同时很多特征都会接近于0。

并行逻辑回归

来源：
由逻辑回归问题的求解方法中可以看出，无论是梯度下降法、牛顿法、拟牛顿法，计算梯度都是其最基本的步骤，并且L-BFGS通过两步循环计算牛顿方向的方法，避免了计算海森矩阵。因此逻辑回归的并行化最主要的就是对目标函数梯度计算的并行化。从公式(2)中可以看出(就是梯度下降法中梯度的计算公式)，目标函数的梯度向量计算中只需要进行向量间的点乘和相加，可以很容易将每个迭代过程拆分成相互独立的计算步骤，由不同的节点进行独立计算，然后归并计算结果。
将M个样本的标签构成一个M维的标签向量，M个N维特征向量构成一个$M\ast N$的样本矩阵，如图3所示。其中特征矩阵每一行为一个特征向量(M行)，列为特征维度(N列)。

图3 样本标签向量 & 样本矩阵

如果将样本矩阵按行划分，将样本特征向量分布到不同的计算节点，由各计算节点完成自己所负责样本的点乘与求和计算(比如一个节点分到一个样本，那么它负责计算$e_1、e_1{x}_{11}、\dots 、e_1{x}_{1p}$;同样第二个节点负责计算$e_2、e_2{x}_{21}、\dots 、e_2{x}_{2p}$;依此类推；每二步进行$e_1+\cdots +e_n;e_1{x}_{11}+e_2{x}_{21}+\cdots +e_n{x}_{n1};\dots$)，然后将计算结果进行归并，则实现了“按行并行的LR”。按行并行的LR解决了样本数量的问题，但是实际情况中会存在针对高维特征向量进行逻辑回归的场景(如广告系统中的特征维度高达上亿)，仅仅按行进行并行处理，无法满足这类场景的需求，因此还需要按列将高维的特征向量拆分成若干小的向量进行求解。

(1) 数据分割

假设所有计算节点排列成m行n列(m*n个计算节点)，按行将样本进行划分，每个计算节点分配M/m个样本特征向量和分类标签；按列对特征向量进行切分，每个节点上的特征向量分配N/n维特征。如图4所示，同一样本的特征对应节点的行号相同，不同样本相同维度的特征对应节点的列号相同。

图4 并行LR中的数据分割

一个样本的特征向量被拆分到同一行不同列的节点中，即：$X_{r,k}=<X_{(r,1),k}>,\dots ,<X_{(r,c),k}>,\dots ,<X_{(r,n),k}>$

其中$X_{r,k}$表示第r行的第k个向量，$X_{(r,c),k}$表示$X_{r,k}$在第c列节点上的分量。同样的，用$W_c$表示特征向量W在第c列节点上的分量，即：$W=<W_1,\dots ,W_c,\dots ,W_n>$

(2) 并行计算

观察目标函数的梯度计算公式(公式(2)),其依赖于两个计算结果：特征权重向量$W_t$和特征向量$X_j$的点乘，标量$[\delta (y_i{W}_t^T{X}_j)-1]y_i$和特征向量$X_j$的相乘。可以将目标函数的梯度计算分成两个并行化计算步骤和两个结果归并步骤：
① 各节点并行计算点乘，计算$d_{(r,c),k,t}=W_{c,t}^T{X}_{(r,c),k}\in R$，其中$k=1,2,\dots ,M/m$，$d_{(r,c),k,t}$表示第t次迭代中节点(r,c)上的第k个特征向量与特征权重分量的点乘，$W_{c,t}$为第t次迭代中特征权重向量在第c列节点上的分量。
② 对行号相同的节点归并点乘结果：

计算得到的点乘结果需要返回到该行所有计算节点中，如图5所示。

图5 点乘结果归并 ③ 各节点独立算标量与特征向量相乘： $G_{(r,c),t}$可以理解为由第r行节点上部分样本计算出的目标函数梯度向量在第c列节点上的分量。

④ 对列号相同的节点进行归并：

$G_{c,t}$就是目标函数的梯度向量$G_t$在第c列节点上的分量，对其进行归并得到目标函数的梯度向量：

这个过程如图6所示。

图6 梯度计算结果归并

综合上述步骤，并行LR的计算流程如图7所示。比较图2和图7，并行LR实际上就是在求解损失函数最优解的过程中，针对寻找损失函数下降方向中的梯度方向计算作了并行化处理，而在利用梯度确定下降方向的过程中也可以采用并行化(如L-BFGS中的两步循环法求牛顿方向)。

图7 并行LR计算流程

实验及结果

利用MPI，分别基于梯度下降法(MPI_GD)和L-BFGS(MPI_L-BFGS)实现并行LR，以Liblinear为基准，比较三种方法的训练效率。Liblinear是一个开源库，其中包括了基于TRON的LR(Liblinear的开发者Chih-Jen Lin于1999年创建了TRON方法，并且在论文中展示单机情况下TRON比L-BFGS效率更高)。由于Liblinear并没有实现并行化(事实上是可以加以改造的)，实验在单机上进行，MPI_GD和MPI_L-BFGS均采用10个进程。

实验数据是200万条训练样本，特征向量的维度为2000，正负样本的比例为3:7。采用十折交叉法比较MPI_GD、MPI_L-BFGS以及Liblinear的分类效果。结果如图8所示，三者几乎没有区别。

图8 分类效果对比

将训练数据由10万逐渐增加到200万，比较三种方法的训练耗时，结果如图9，MPI_GD由于收敛速度慢，尽管采用10个进程，单机上的表现依旧弱于Liblinear，基本上都需要30轮左右的迭代才能达到收敛；MPI_L-BFGS则只需要3~5轮迭代即可收敛(与Liblinear接近)，虽然每轮迭代需要额外的开销计算牛顿方向，其收敛速度也要远远快于MPI_GD，另外由于采用多进程并行处理，耗时也远低于Liblinear。

图9 训练耗时对比

使用spark建立逻辑回归(Logistic)模型帮Helen找男朋友

来源：https://blog.csdn.net/u013719780/article/details/52277616
作者使用得不太好，但可以参考一下，自己做改进。而且spark中逻辑回归实现了多分类算法。

为什么逻辑回归比线性回归要好？

https://blog.csdn.net/cyh_24/article/details/50359055

逻辑回归与最大熵模型MaxEnt的关系?

简单粗暴 的回答是：逻辑回归跟最大熵模型没有本质区别。逻辑回归是最大熵对应类别为二类时的特殊情况，也就是当逻辑回归类别扩展到多类别时，就是最大熵模型。

最大熵模型是约束条件下的熵最大化，可以通过拉格朗日乘子进行推导。可得到最大似然的形式。
而逻辑回归就是最大熵模型k=2的特性。

逻辑回归的python实现

逻辑回归使用心得

scikit-learn 逻辑回归类库使用小结

逻辑回归应用之Kaggle泰坦尼克之灾

来源：https://blog.csdn.net/han_xiaoyang/article/details/49797143
很详细的一个案例，尤其是最后的逻辑回归系统优化部分有时间要练习一下，自己目前还没有真正花心思去优化已经实现的模型。

其他参考资料：

深入解读Logistic回归结果(一)：回归系数，OR

逻辑回归的前世今生
Logistic Regression 的前世今生(理论篇)

《Logistic Regression 模型简介》，来源：FIN ·2015-05-08 10:00
Python实现逻辑回归(Logistic Regression in Python)