Learning monocular visual odometry with dense 3D mapping from dense 3D flow

IROS深度学习定位论文2_深度学习SLAM

论文：Learning monocular visual odometry with dense 3D mapping from dense 3D flow
地址：https://arxiv.org/pdf/1803.02286.pdf

1 摘要

  本文所介绍的论文提出了一种完全由深度学习实现的单目SLAM，可以同时进行定位并进行稠密3D建图。通过将单目图像的2D光流以及深度图像作为两个子模型，然后利用L-VO模型的关联层将这两个子模型融合，形成3D稠密光流。基于3D稠密光流，本文提出的L-VO模型可以实现6DOF相对位姿估计并重建相机轨迹。为了学习运动方向的关联关系，作者采用基于二元高斯建模的损失函数。在KITTI数据集上进行实验，结果表明作者提出的方法的位移误差为2.68%，旋转误差为0.0143度/m。除此以外，作者通过学习深度信息生成稠密的3D八叉树地图。由此可见，该论文所介绍的方法是一种完整的视觉SLAM系统，能够从单目图像进行稠密3D建图。

2 实验结果

2.1 数据集

  数据集采用KITTI VO/SLAM benchmark，包括22段序列，其中00-10提供误差小于10cm的真值，11-21仅包含原始的传感器数据，没有标注真值。

2.2 模型训练与测试

  采用Adam优化器；batch_size=100；动量因子固定为(0.9, 0.999)；初始学习率为0.0001，学习率衰减因子为0.95；总共训练100epochs；采用了来自文献[25][26]预训练的模型。在训练时，对图像进行4倍下采样（320x96），论文指出进行这样的下采样会降低模型的性能，但会提升模型的训练效率。除此以外，对训练数据进行了几何增强（translation/totation/scaling）以及图像增强（color/brightness/gamma）。在测试阶段，将高斯样本的数量设置为10000。

2.3 视觉里程计的性能

  **评价1：**对于00~10有真值的KITTI数据集，利用00，02，08，09序列数据进行训练，并利用剩余的03，04，05，06，07，10序列数据进行测试。实验结果包括轨迹定性分析以及误差定量分析两部分，分别如下所示。


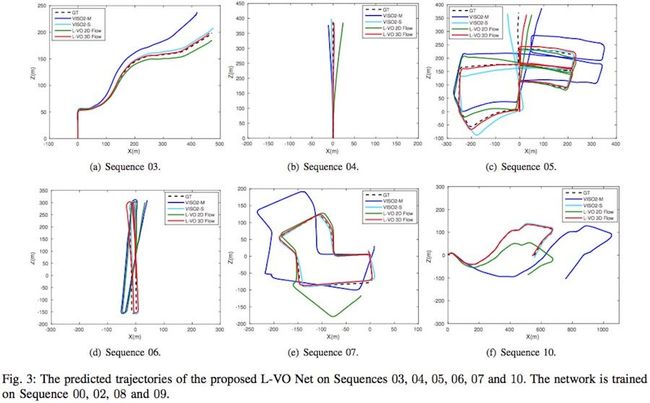
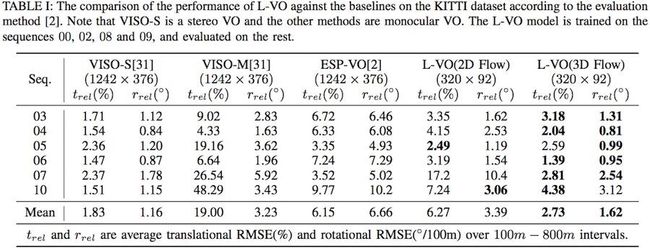
  **评价2：**利用00-10有真值的KITTI数据集作为训练数据，11-21序列无真值数据作为测试数据，并定性评估其轨迹，结果如下：

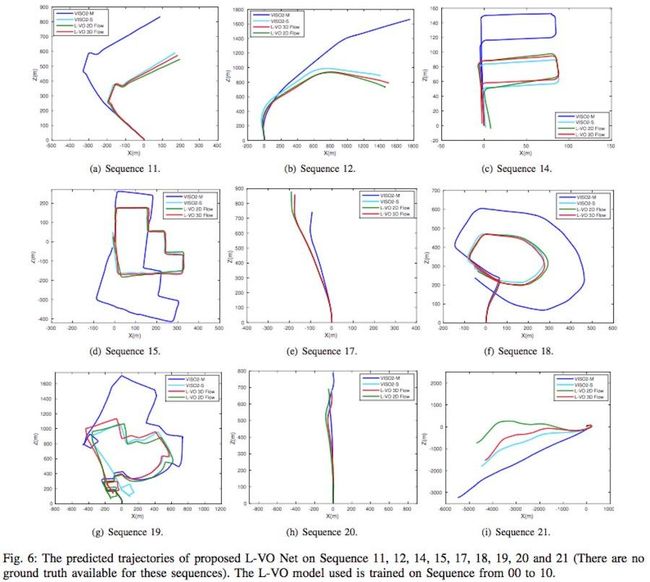
3 方法

3.1 L-VO模型结构

  论文中所提出的L-VO模型结构如下所示。该模型结构能同时实现单目图像的位姿估计和3D地图构建。L-VO模型的输入为Depth Map和2D Flow，输出是单目图像姿态，其中的Depth Map和2D Flow分别来自模型DepthNet和FlowNet2。首先，L-VO模型将Depth Map和2D Flow融合为3D Flow；然后，3D Flow被送入两个独立的模型分支，其中一个分支用于估计相邻两帧图像的相对位移量和相对旋转量。同时，根据估计的图像深度进行点云生成，然后对3D点云进行精调以去除外点和不正确的预测点，最后在利用八叉树进行稠密地图的生成。

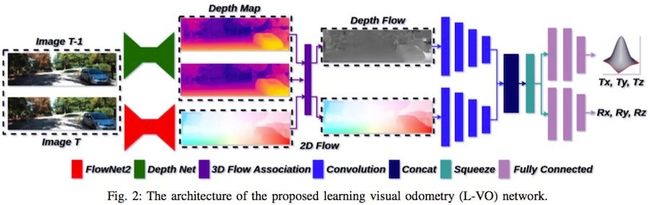
3.2 Depth Map和2D Flow的估计

  Depth Map和2D Flow直接由文献[25]FlowNet2和文献[26]DepthNet提出的模型获取，同时在KITTI数据集上对模型进行微调。

3.3 3D Flow关联层

  假设$F_{XY}^{k:k+1}\in {\mathbb{R}}^{h\times w\times 2}$代表图像k与图像k+1在X-Y图像平面上的2D Flow；$D^k\in {\mathbb{R}}^{h\times w}$代表图像k的深度图，那么3D Flow关联层可定义如下：
$$\begin{gathered} F_Z^{k:k+1}(x,y)=D^{k+1}((x,y)+F_{XY}^{k:k+1})-D^k(x,y) \\ {F}_{3D}^{k:k+1}=\mathcal{C}(F_{XY}^{k:k+1},F_Z^{k:k+1}) \end{gathered}$$
其中，$F_{3D}^{k:k+1}\in {\mathbb{R}}^3$是对应于像素(x,y)坐标的3D Flow；$\mathcal{C}$代表concatenation操作。备注：图像k+1的深度值存在无法与图像k对应的深度，作者采用插值的方式进行填补；同时，值得注意的是，这里的深度均指代逆深度（逆深度可以减小离相机较远的深度的重要性，提高离相机较近点的敏感度）。

3.4 里程计学习

  里程计学习模型采用相同的两个分支网络进行实现，如L-VO模型结构中蓝色部分。总共包括四个卷积层，channels数分别为64、128、256和512，卷积核为3x3，stride为2，这个网络结构为了保留空间信息并没有使用池化层。最后，将两个分支进行concatenation并利用1x1卷积核进行squeeze。可形式化表示为如下形式：
$$F_{3D}=\mathcal{S}(F_{XY},F_Z)$$
  其中$\mathcal{S}$代表squeeze操作；$F_{XY}\in {\mathbb{R}}^{h\times w\times n}$和$F_Z\in {\mathbb{R}}^{h\times w\times n}$分别代表2D Flow和Depth Flow；输出$F_{3D} \in \mathbb R^{h \times w \times n \setminus 4} $为squeeze特征，n为channel数量。squeeze层实现了3D特征的低维嵌入，减少了回归的输入数据维度。接着，里程计学习模型最后接了2个三层全连接层分别用于位置和姿态的回归；其中的隐藏层神经单元为128并采用relu激活函数。值得注意的是位置回归分支采用了二元高斯函数（为了学习时序之间的关系）进行描述，所以需要回归6个维度；而姿态回归分支则输出3个欧拉角。

3.5 二元高斯损失函数

  这里的二元损失函数是本论文的创新点，也是我认为该论文的方法通用性不强的原因。论文作者描述的二元损失函数是一种假设，具体为在室外道路驾驶的汽车，其水平面的坐标轴的位移具有强相关性。基于此，作者设计了一种促使网络学习车辆前向和左右向的位移的方法，这里使用的就是二元高斯损失函数。
  针对KITTI数据集，作者将车辆正前方设为z轴，水平向右设为x轴，根据右手坐标系可知y轴垂直向下。因此，y轴变化量相对于x,z轴的变化量将比较小，y轴将直接进行回归，而x,z轴则使用二元高斯函数进行描述。值得注意的是，该论文所回归的旋转量并非四元数，而是欧拉角，给出的理由是四元数作为标签容易造成模型训练的过拟合。综合起来，论文所提出模型的损失函数如下所示：
$$\begin{gathered} loss=\sum _i^N-log(PDF(x_{gt}^i,z_{gt}^i),{\mathcal{N}}^i(\mu ,\Sigma )) \\ +{\lambda }_1\sum _i^N||y_p^i-y_{gt}^i|{|}_2+{\lambda }_2\sum _i^N||r_p^i-r_{gt}^i|{|}_2+{\lambda }_3||W|{|}_2 \end{gathered}$$

  其中$(x_{gt}^i,y_{gt}^i,z_{gt}^i)$为相机位移真值，$(x_p^i,y_p^i,z_p^i)$为第i个图像/相机的预测位移。$r_p^i:=(r_p^x,r_p^y,r_p^z{)}^i$和$r_{gt}^i:=(r_{gt}^x,r_{gt}^y,r_{gt}^z{)}^i$分别代表欧拉角的预测值和真值。${\lambda }_1,{\lambda }_2,{\lambda }_3$代表尺度因子。
  x,z轴二元高斯密度函数定义如下：
$$\begin{gathered} PDF((x_{gt}^i,z_{gt}^i),{\mathcal{N}}^i(\mu ,\Sigma ))= \\ \frac{exp(-\frac{1}{2}((x_{gt}^i,z_{gt}^i)-\mu ){\Sigma }^{-1}((x_{gt}^i,z_{gt}^i)-\mu {)}^T)}{((2\pi {)}^2|\Sigma |{)}^{-\frac{1}{2}}} \end{gathered}$$
  其中二元高斯分布$\mathcal{N}$的均值和方差分别为：
$$\mu =({\mu }_x,{\mu }_z{)}^i,\Sigma ={\left\{\begin{array}{cc}{\sigma }_x^2& \rho {\sigma }_x{\sigma }_z\\ \rho {\sigma }_x{\sigma }_z& {\sigma }_z^2\end{array}\right\}}^i$$
  其中${\mu }_x,{\mu }_z$分别为车辆左右向和前向的均值，${\sigma }_x,{\sigma }_z$分别为车辆左右向和前向的标准差，$\rho$为车辆平面左右向和前向的关联系数。由此可见，神经网络需要学习的位置参数为$({\mu }_x,{\mu }_z,{\sigma }_x,{\sigma }_z,\rho ,y_p)$，姿态参数为$(e_p^z,e_p^y,e_p^x)$。当神经网络输出预测的位置参数后，对应的位置量$x,z$即可计算出来，具体如下：
$$x,z=\frac{1}{N_s}\sum _k^{N_s}(x_s,z_s{)}^k\sim {\mathcal{N}}_p(\mu ,\Sigma )$$
  其中${\mathcal{N}}_p$来自模型预测的$({\mu }_x,{\mu }_z,{\sigma }_x,{\sigma }_z,\rho ,y_p)$，$(x_s,z_s{)}^k$为第k个样本，$N_s$为样本数量。

3.6 利用八叉树深度融合的建图

  作者提出了一种利用位姿与深度进行3D稠密建图的方法。当给定一种RGB图像和对应预测的深度图像，以相机光心为世界坐标系原点而构建的3D点云可由如下公式给出：
$$d_{u,v}\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& s& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$$
  其中$f_x,f_y$是焦距，$(c_x,cy)$是相机主点（光心），$s$is the axis skew，$(u,v)$是图像坐标系中的像素位置。
  实际上，模型所预测的深度在深度边缘常不太准确，因此不能直接用于3D建图。本文的作者使用文献[30]提出的OctoMap进行3D模型的精调和维护。OctoMap解决的问题是确定八叉树叶子节点是否可以用于建图的概率，如果某个叶子节点的概率大于阈值，则将该叶子节点用于建图。形式化表示为：假设OctoMap的某个叶子节点为n，当给定多个时刻的某个3D点（对应叶子节点n）测量值$o_{1:t}$时，则其用于建图的概率$P(n|o_{1:t})$（Probabilistic Sensor Fusion）可由如下公式进行计算：
$$P(n|o_{1:t})={\left[\begin{array}{c}1+\frac{1-P(n|o_t)}{P(n|o_t)}\frac{1-P(n|o_{1:t-1})}{P(n|o_{1:t-1})}\frac{1-P(n)}{P(n)}\end{array}\right]}^{-1}$$
  由以上概率公式就可以融合多个视角（多个时刻）拍摄图像的深度估计，并能根据概率公式滤除预测深度不准确的3D点。

4 结论与评价

  本论文提出了一种同时估计单目相机的位姿并进行八叉树稠密建图的端到端深度学习方法。论文主要做了2方面的贡献，一是结合2D Flow和2D Depth解决单目尺度不确定的问题，同时设计了一种L-VO模型用于位姿的估计；二是针对KITTI数据集（或道路上行驶的车辆摄像头）做了合理的假设（将车辆正前方设为z轴，水平向右设为x轴，根据右手坐标系可知y轴垂直向下），认为车辆行驶的前向z和左右向x具有强相关性，并利用二元高斯函数描述它们之间的关系，将模型估计的位置变量变为$({\mu }_x,{\mu }_z,{\sigma }_x,{\sigma }_z,\rho ,y_p)$，最后再利用二元高斯函数进行x,z值的恢复。
  这篇论文，其创新点既是亮点也是它的缺点，即将问题限制到了道路上行驶车辆摄像头位置估计的问题，这样会使得该深度学习SLAM更适合解决特定场景问题，通用性不太强。总体来看，论文所做工作还是值得肯定的，如：模型集成解决尺度问题和特定条件下问题的合理假设等。