数学建模 - 01背包问题多种解法 | C语言、Matlab、Lingo
别问我一个大学生暑假为什么只放二十几天,问就是数学建模!
好吧其实建模还是挺有意思的,通过学习我掌握了多种计算机语言。前几天的课上讲到了背包问题,只讲了数学上的讲法,没说代码怎么写。当时脑子一热想出了一种特殊的算法,虽然之后的课上讲到了这种想法,但是我还是花了一个下午的时间在讲之前把01背包问题的C语言解法写了出来。讲完后,我今天又把典型背包问题的Lingo和Matlab解法完成了。下面讲讲解法和思路吧!
背包问题
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题,即在总重量不超过W的前提下,总价值是否能达到V?(摘自百度百科)
对于背包问题分为以下三类:
一、01背包
01背包即每种物品的数量为1,可以选择放或者不放,这可以转化为二进制中的0和1,而C语言代码对于0和1的枚举是极其方便的,因为他的时间复杂度为O(2^n)。对于常规的背包问题涉及的物品不会特别多,6个以下的问题纯手算都可以轻松解决,而当今的计算机运算速度都非常快,一般15个物品循环6W多次只要0.8秒左右的时间。单纯的枚举不需要考虑很多方面的因素,而在设定了限制条件之后,可以转化成隐枚举的方法缩短运行时间。
对于01背包的C语言思路:
- 建立一个item结构体储存每个物品的质量和价值。
- 定义一个数组储存倒序的二进制排列数。为什么是倒序的呢?因为十进制数转化为二进制的算法计算出来的二进制是倒序排列的,而倒序恰好也符合了人的思维模式,即从取第一个物品开始(10)而不是最后一个(01)。
- 输入各项数据,根据算法的复杂度
O(2^n)开始循环,一共产生2^n种排列,对于每种排列计算出该方案的总重量和总价值。 - 设置重量条件,符合限制条件后比较总价值与最高价值,保留最大值。
代码如下:
//
// main.c
// Knapsack Question
//
// Created by Kevin on 2019/6/26.
// Copyright © 2019 ZeKai Jia. All rights reserved.
//
#include
#include
struct Item {
int Weight;
int Value;
}item[100];
int main(void) {
int Boo[40000][16]={0}; //储存排列,注意空间
int TotalWeight, TotalValue;
int Number, Capacity, MaxValue = 0; //初始化最高价值
int i, n, k, j = -1;
printf("Total number of the items:");
scanf("%d",&Number);
printf("Input each item's Weight:");
for ( i=0; i0 ) {
Boo[n][i] = k%2;
i += 1;
k /= 2;
}
}
k = n;
for ( n=0; n= MaxValue) {
MaxValue = TotalValue;
j = n;
}
}
}
}
if ( j == -1 ) {
printf("No solution!\n");
}
else {
printf("The roots are:");
for ( i=0; i 大致就是如此,其实这个程序还有缺陷,第一个就是数组储存在栈中,只可以计算16个以下的物品数,当然电脑不同可能有所差异。所以如果想计算足够多的物品,切记要使用 malloc 把数据存储在堆中。
第二个问题就是它仅能处理01问题,对于其他背包问题就无力解决啦,毕竟一旦物品数量设定为k值,复杂度就提升到了O((k+1)^n),恐怕不是超级计算机的话是难以解决这类问题了。所以咱们点到为止,接着下一种背包问题。
补充:
今天我把01背包问题使用 Lingo 进行了求解,由于 Lingo 是专业求解线性和非线性优化问题的软件,属于黑箱模式,我们只需要把题目的条件输入程序就会自动求解,所以代码相当少。唯一的缺点就是对不同题目需要修改代码中的数据,不能像 C 一样读取用户输入的数据进行操作。
代码如下:
model:
sets:
a/1..7/: Weight, Value, Capacity ; //设置 n 个同类元素集合
endsets
data :
Weight = 31 10 20 19 4 3 6;
Value = 70 20 39 37 7 5 10;
enddata
max = @sum(a :Value*Capacity) ;
@sum(a : Weight*Capacity) <= 50 ; //总重量不超过50的背包
@for(a:@bin(Capacity)) ;
end
End
二、完全背包
在完全背包问题中,所有的物品都有无限次数可用。显而易见的是在这种情况下背包中存放质价比最高的物品最划算,但是最后一件物品并不见得能塞得下这个背包,于是需要挑出这件物品放入质价比较前者低同时质量也较轻的物品。总之,我们要利用乌鸦喝水的思路尽可能多地塞满(不一定能满)背包,并且使总价值最高。
对于完全背包的Matlab思路:
建立动态规划表,例如一个背包容量为5的表格
| item | weight | value | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|
| a | 2 | 7 | 0 | 3 | 7 | 11 | 14 | 18 |
| b | 1 | 3 | 0 | 3 | 6 | 11 | 14 | 17 |
| c | 3 | 11 | 0 | 0 | 0 | 11 | 11 | 11 |
我们令 W i 表示物品质量,V i 表示物品价值
循环阶段:
i = 1 , 2 , 3 i = 1,2,3 i=1,2,3
第 i 阶段检查第 i 个物品
状态变量:
S i S_i Si i = 1 , 2 , 3 i= 1,2,3 i=1,2,3
检查 i 物品时的剩余空间
决策变量:
X i X_i Xi i = 1 , 2 , 3 i=1,2,3 i=1,2,3
第 i 个物品装入量
状态转移方程:
S i + 1 = S i − W i X i S_{i+1}=S_i - W_iX_i Si+1=Si−WiXi
最优值函数:
f ( S i ) f(S_i) f(Si)
最优值函数转移方程:
f ( S i ) W i X i ≤ S i = V i X i + f ( S i + 1 ) i = 1 , 2 V i X i i = 3 {f(S_i)\over{W_iX_i \leq S_i}}={V_iX_i+f(S_i+1) \quad i=1,2 \over V_iX_i \quad \quad \quad \quad \quad \ i=3} WiXi≤Sif(Si)=ViXi i=3ViXi+f(Si+1)i=1,2
这样一来就可以对方程求解了,但是需要逆推,下面的工作全部交给我们的Matlab处理即可。
代码如下:
function Knapsack_Question_Fun(n,Capacity,Weight,Value)
f=zeros(n,Capacity+1);x=zeros(n,Capacity+1);xx=zeros(n,1);
for i=n:-1:1
for S=0:Capacity
if i==7
f(i,S+1)=Value(i)*floor(S/Weight(i));
x(i,S+1)=floor(S/Weight(i));
else
xMax=floor(S/Weight(i));
ff=zeros(xMax+1,1);
for k=0:xMax
ff(k+1)=Value(i)*k+f(i+1,S-Weight(i)*k+1);
end
[f(i,S+1),index]=max(ff);
x(i,S+1)=index-1;
end
end
end
[optValue,index]=max(f(1,:));
xx(1)=x(1,index);
tempS=index;
fprintf('optimal solution:%d\n',optValue);
for i=2:7
xx(i)=x(i,tempS-Weight(i-1)*xx(i-1));
tempS=tempS-Weight(i-1)*xx(i-1);
end
for i=1:n
fprintf('put %d item%d in the bag\n',xx(i),i);
end
end
上面这个是函数文件,我们还需要将数据输入在 Excel 表格中,然后使用以下脚本读取并调用函数:
n = input('Total number of the items:'); //输入物品数量
strn = n;
W = 'a2:a'; V = 'b2:b';
strn = num2str(strn+1); //将数量转换成最后一个单元格的代号
W = [W strn]; V = [V strn]; //生成读取范围
Weight = xlsread('BQVar.xlsx',W);
Value = xlsread('BQVar.xlsx',V);
Capacity = xlsread('BQVar.xlsx','c2:c2');
Weight';Value'; //转置成行向量
Knapsack_Question_Fun(n,Capacity,Weight,Value)
以下为 Excel 中的填写格式:
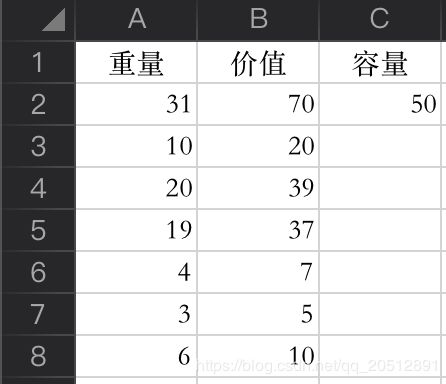
开始比较难,但是完成之后就可以直接套用模板求解背包问题了,照着图中的方式填写条件即可,非常方便!
多重背包
多重背包是01背包和完全背包的中间形态,每一种物品的数量有 1-k 个,所以对于每种物品其可取值为 0-k 个。多重背包问题即是在完全背包问题的基础上添加了多个限制条件,具体代码就不给大家了,直接对完全背包中 Matlab 的代码进行修改即可。
其实解这一类问题还有一种方法,那就是将其转化为01背包问题:把第 i 种物品换成 n 件01背包中的物品,则得到了物品数为∑n的01背包问题,直接求解,复杂度仍然是O(V*∑n)。如果想让它像01背包一样能够使用二进制算法,就要考虑把第 i 种物品换成若干件物品,使得原问题中第 i 种物品可取的每种策略均能等价于取若干件代换以后的物品,并且不能使取超过 n 件的策略出现。例如取 1,2,4 三种数量级,一件物品有 12 件,那么这件物品可取件数是 1,2,4,5 ,然后将其质量和价值也乘以对应系数,将时间复杂度降低到了O(V*∑log n。此处也是抛砖引玉,大家可以去尝试一下,但我个人而言还是比较相信计算机的处理能力,原始的方法复杂度高但是对计算机而言还是分分钟就能解决的问题。
总结
小小的背包问题,在运筹学、密码学等领域有着大大的作用。背包问题的算法多种多样,大家各取所需吧。我作为一名初学者,Matlab 和 Lingo 代码写得并不好,欢迎大家指教,之后如果有更好的想法和代码我会及时补充。