物理模拟与taichi编程实现
1 物理模拟的需求背景
随着人工智能时代的迅速发展,出现了两种范式的人工智能。与之相对应的是大数据与大任务平台。
对于以数据为中心的传统人工智能发展出现瓶颈,而以大任务为中心的通用的人工智能有很大的优越性。对于任务的表达就需要用物理模拟的方式来体现真实的物理环境。
1.1 传统人工智能
1 传统的人工智能是以大数据为中心。以其代表的观点是AI = Big data + computering power + deep learning。
2 传统的人工智能存在很多问题,必须以大量数据为前提,只能做一些特定的人类事先定义好的任务,而无法完成通用任务。此外,每项任务需要大量的数据,成本非常高,而且模型不具有解释性,知识表达与人不同。每次模型的建立都需要大量的训练,测试数据来搭建模型,效率比较低。
3.传统的人能智能对应于其特点是大数据小任务。
1.2 通用人工智能
1.通用的人工智能是以任务为中心表现的智能。
对应的以任务为中心的表达方式的构建。
2.对于任务的定义,有关物理流态与社会流态仿真的实现需借助物理模拟的方法来真实的体现。
3.对于搭建大任务平台,以物理模拟虚拟场景与AI结合是其必然趋势。只在一个物理场景中训练是不够的。第一步要根据人的需求,生成大量的数据库中的三维物体。这也是使用物理模拟来搭建。对于物理的逼真环境需要用动态的偏微分方程实现。
4.其对应的特点是小数据,大任务。重点是通过任务来训练学习,感知,推理。
2 taichi编程环境来进行的物理模拟
2.1 taichi环境的引出
1.三维体积数据通常具有空间稀疏性。为了利用这种性质,计算机图形学社区开发了层级体素稀疏数据结构,如SPGrid、VDB和八叉树等。但是,由于其内在复杂性和额外开销,开发、应用这些高性能数据结构有很多挑战。提出Taichi,一个新的面向(稀疏)数据的编程语言,大大降低了空间稀疏数据结构的开发、使用成本。
2.由于Taichi实现了算法和数据结构的解耦,使用者可以快速尝试不同数据结构,以在特定问题和体系结构上找到最优数据结构。语言前端提供给用户易用的接口,使得用户可以以访问稠密数据结构的方式访问稀疏数据结构,大大提高了代码可读性和生产力。
3.Taichi编译器使用对数据结构的语义和下标分析来优化程序的局部性,移除多余数据结构遍历,以及进行自动内存管理和并行化、向量化。在x86_64和CUDA体系结构上,只需要1/10的代码,Taichi程序就能比手动优化的稀疏计算基准程序快4.55倍,
4.可用于包括物质点法、有限元模拟、多重网格泊松方程求解,真实感渲染,和3D稀疏卷积神经网络等。
2.2 编译环境的搭建
1.Python 3.6/3.7 needed
2.CPU only. No GPU/CUDA needed. (Linux, OS X and Windows)
python3 -m pip install taichi-nightly
With GPU (CUDA 10.0) support (Linux only)
python3 -m pip install taichi-nightly-cuda-10-0
With GPU (CUDA 10.1) support (Linux only)
python3 -m pip install taichi-nightly-cuda-10-1
注意:对于安装失败,对于我的机子,已安装cuda10.1版本。是重新换镜像源来安装成功,具体的shell命令如下:
pip3 install taichi-nightly-cuda-10-1 -i https://pypi.tuna.tsinghua.edu.cn/simple
pip3 install taichi-nightly -i https://pypi.tuna.tsinghua.edu.cn/simple
2.3 利用taichi编译环境实现的demo
2.3.1 利用c++实现的MLS-MPM(移动最小二乘的物质点法)
1.所使用的环境
1)系统:可以是debian10,windows,mac os x 10.11-10.14,ubuntu16,ubuntu18
2)必须包含taichi.h
2.编译运行命令
1)
* Linux:
g++ mls-mpm88.cpp -std=c++14 -g -lX11 -lpthread -O3 -o mls-mpm
./mls-mpm
* Windows (MinGW):
g++ mls-mpm88.cpp -std=c++14 -lgdi32 -lpthread -O3 -o mls-mpm
.\mls-mpm.exe
OS X:
g++ mls-mpm88.cpp -std=c++14 -framework Cocoa -lpthread -O3 -o mls-mpm
./mls-mpm
对于我的debian出现报错如下:

解决方式:由于缺少对应的lgdi32库。必须安装并添加
sudo apt-cache search x11-dev
sudo apt-get install libghc-x11-dev
g++ mls-mpm88.cpp -std=c++14 -g -lX11 -lpthread -O3 -o mls-mpm
./mls-mpm
3.代码
//88-Line 2D Moving Least Squares Material Point Method (MLS-MPM)[with comments]
//#define TC_IMAGE_IO // Uncomment this line for image exporting functionality
#include "taichi.h" // Note: You DO NOT have to install taichi or taichi_mpm.
using namespace taichi;// You only need [taichi.h] - see below for instructions.
const int n = 80 /*grid resolution (cells)*/, window_size = 800;
const real dt = 1e-4_f, frame_dt = 1e-3_f, dx = 1.0_f / n, inv_dx = 1.0_f / dx;
auto particle_mass = 1.0_f, vol = 1.0_f;
auto hardening = 10.0_f, E = 1e4_f, nu = 0.2_f;
real mu_0 = E / (2 * (1 + nu)), lambda_0 = E * nu / ((1+nu) * (1 - 2 * nu));
using Vec = Vector2; using Mat = Matrix2; bool plastic = true;
struct Particle { Vec x, v; Mat F, C; real Jp; int c/*color*/;
Particle(Vec x, int c, Vec v=Vec(0)) : x(x), v(v), F(1), C(0), Jp(1), c(c){}};
std::vector<Particle> particles;
Vector3 grid[n + 1][n + 1]; // velocity + mass, node_res = cell_res + 1
void advance(real dt) {
std::memset(grid, 0, sizeof(grid)); // Reset grid
for (auto &p : particles) { // P2G
Vector2i base_coord=(p.x*inv_dx-Vec(0.5_f)).cast<int>();//element-wise floor
Vec fx = p.x * inv_dx - base_coord.cast<real>();
// Quadratic kernels [http://mpm.graphics Eqn. 123, with x=fx, fx-1,fx-2]
Vec w[3]{Vec(0.5) * sqr(Vec(1.5) - fx), Vec(0.75) - sqr(fx - Vec(1.0)),
Vec(0.5) * sqr(fx - Vec(0.5))};
auto e = std::exp(hardening * (1.0_f - p.Jp)), mu=mu_0*e, lambda=lambda_0*e;
real J = determinant(p.F); // Current volume
Mat r, s; polar_decomp(p.F, r, s); //Polar decomp. for fixed corotated model
auto stress = // Cauchy stress times dt and inv_dx
-4*inv_dx*inv_dx*dt*vol*(2*mu*(p.F-r) * transposed(p.F)+lambda*(J-1)*J);
auto affine = stress+particle_mass*p.C;
for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) { // Scatter to grid
auto dpos = (Vec(i, j) - fx) * dx;
Vector3 mv(p.v * particle_mass, particle_mass); //translational momentum
grid[base_coord.x + i][base_coord.y + j] +=
w[i].x*w[j].y * (mv + Vector3(affine*dpos, 0));
}
}
for(int i = 0; i <= n; i++) for(int j = 0; j <= n; j++) { //For all grid nodes
auto &g = grid[i][j];
if (g[2] > 0) { // No need for epsilon here
g /= g[2]; // Normalize by mass
g += dt * Vector3(0, -200, 0); // Gravity
real boundary=0.05,x=(real)i/n,y=real(j)/n; //boundary thick.,node coord
if (x < boundary||x > 1-boundary||y > 1-boundary) g=Vector3(0); //Sticky
if (y < boundary) g[1] = std::max(0.0_f, g[1]); //"Separate"
}
}
for (auto &p : particles) { // Grid to particle
Vector2i base_coord=(p.x*inv_dx-Vec(0.5_f)).cast<int>();//element-wise floor
Vec fx = p.x * inv_dx - base_coord.cast<real>();
Vec w[3]{Vec(0.5) * sqr(Vec(1.5) - fx), Vec(0.75) - sqr(fx - Vec(1.0)),
Vec(0.5) * sqr(fx - Vec(0.5))};
p.C = Mat(0); p.v = Vec(0);
for (int i = 0; i < 3; i++) for (int j = 0; j < 3; j++) {
auto dpos = (Vec(i, j) - fx),
grid_v = Vec(grid[base_coord.x + i][base_coord.y + j]);
auto weight = w[i].x * w[j].y;
p.v += weight * grid_v; // Velocity
p.C += 4 * inv_dx * Mat::outer_product(weight * grid_v, dpos); // APIC C
}
p.x += dt * p.v; // Advection
auto F = (Mat(1) + dt * p.C) * p.F; // MLS-MPM F-update
Mat svd_u, sig, svd_v; svd(F, svd_u, sig, svd_v);
for (int i = 0; i < 2 * int(plastic); i++) // Snow Plasticity
sig[i][i] = clamp(sig[i][i], 1.0_f - 2.5e-2_f, 1.0_f + 7.5e-3_f);
real oldJ = determinant(F); F = svd_u * sig * transposed(svd_v);
real Jp_new = clamp(p.Jp * oldJ / determinant(F), 0.6_f, 20.0_f);
p.Jp = Jp_new; p.F = F;
}
}
void add_object(Vec center, int c) { // Seed particles with position and color
for (int i = 0; i < 500; i++) // Randomly sample 1000 particles in the square
particles.push_back(Particle((Vec::rand()*2.0_f-Vec(1))*0.08_f + center, c));
}
int main() {
GUI gui("Real-time 2D MLS-MPM", window_size, window_size);
add_object(Vec(0.55,0.45), 0xED553B); add_object(Vec(0.45,0.65), 0xF2B134);
add_object(Vec(0.55,0.85), 0x068587); auto &canvas = gui.get_canvas();int f=0;
for (int i = 0;; i++) { // Main Loop
advance(dt); // Advance simulation
if (i % int(frame_dt / dt) == 0) { // Visualize frame
canvas.clear(0x112F41); // Clear background
canvas.rect(Vec(0.04), Vec(0.96)).radius(2).color(0x4FB99F).close();// Box
for(auto p:particles)canvas.circle(p.x).radius(2).color(p.c);//Particles
gui.update(); // Update image
// canvas.img.write_as_image(fmt::format("tmp/{:05d}.png", f++));
}
}
}
2.3.2 利用python实现的MLS-MPM(移动最小二乘的物质点法)
1.编译命令
实现先需安装taichi库:
然后编译运行:
python3 <文件名.py>
2.代码
import taichi as ti
quality = 1 # Use a larger value for higher-res simulations
n_particles, n_grid = 9000 * quality ** 2, 128 * quality
dx, inv_dx = 1 / n_grid, float(n_grid)
dt = 1e-4 / quality
p_vol, p_rho = (dx * 0.5)**2, 1
p_mass = p_vol * p_rho
E, nu = 0.1e4, 0.2 # Young's modulus and Poisson's ratio
mu_0, lambda_0 = E / (2 * (1 + nu)), E * nu / ((1+nu) * (1 - 2 * nu)) # Lame parameters
x = ti.Vector(2, dt=ti.f32, shape=n_particles) # position
v = ti.Vector(2, dt=ti.f32, shape=n_particles) # velocity
C = ti.Matrix(2, 2, dt=ti.f32, shape=n_particles) # affine velocity field
F = ti.Matrix(2, 2, dt=ti.f32, shape=n_particles) # deformation gradient
material = ti.var(dt=ti.i32, shape=n_particles) # material id
Jp = ti.var(dt=ti.f32, shape=n_particles) # plastic deformation
grid_v = ti.Vector(2, dt=ti.f32, shape=(n_grid, n_grid)) # grid node momemtum/velocity
grid_m = ti.var(dt=ti.f32, shape=(n_grid, n_grid)) # grid node mass
ti.cfg.arch = ti.cuda # Try to run on GPU
@ti.kernel
def substep():
for i, j in ti.ndrange(n_grid, n_grid):
grid_v[i, j] = [0, 0]
grid_m[i, j] = 0
for p in range(n_particles): # Particle state update and scatter to grid (P2G)
base = (x[p] * inv_dx - 0.5).cast(int)
fx = x[p] * inv_dx - base.cast(float)
# Quadratic kernels [http://mpm.graphics Eqn. 123, with x=fx, fx-1,fx-2]
w = [0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1), 0.5 * ti.sqr(fx - 0.5)]
F[p] = (ti.Matrix.identity(ti.f32, 2) + dt * C[p]) @ F[p] # deformation gradient update
h = ti.exp(10 * (1.0 - Jp[p])) # Hardening coefficient: snow gets harder when compressed
if material[p] == 1: # jelly, make it softer
h = 0.3
mu, la = mu_0 * h, lambda_0 * h
if material[p] == 0: # liquid
mu = 0.0
U, sig, V = ti.svd(F[p])
J = 1.0
for d in ti.static(range(2)):
new_sig = sig[d, d]
if material[p] == 2: # Snow
new_sig = min(max(sig[d, d], 1 - 2.5e-2), 1 + 4.5e-3) # Plasticity
Jp[p] *= sig[d, d] / new_sig
sig[d, d] = new_sig
J *= new_sig
if material[p] == 0: # Reset deformation gradient to avoid numerical instability
F[p] = ti.Matrix.identity(ti.f32, 2) * ti.sqrt(J)
elif material[p] == 2:
F[p] = U @ sig @ V.T() # Reconstruct elastic deformation gradient after plasticity
stress = 2 * mu * (F[p] - U @ V.T()) @ F[p].T() + ti.Matrix.identity(ti.f32, 2) * la * J * (J - 1)
stress = (-dt * p_vol * 4 * inv_dx * inv_dx) * stress
affine = stress + p_mass * C[p]
for i, j in ti.static(ti.ndrange(3, 3)): # Loop over 3x3 grid node neighborhood
offset = ti.Vector([i, j])
dpos = (offset.cast(float) - fx) * dx
weight = w[i][0] * w[j][1]
grid_v[base + offset] += weight * (p_mass * v[p] + affine @ dpos)
grid_m[base + offset] += weight * p_mass
for i, j in ti.ndrange(n_grid, n_grid):
if grid_m[i, j] > 0: # No need for epsilon here
grid_v[i, j] = (1 / grid_m[i, j]) * grid_v[i, j] # Momentum to velocity
grid_v[i, j][1] -= dt * 50 # gravity
if i < 3 and grid_v[i, j][0] < 0: grid_v[i, j][0] = 0 # Boundary conditions
if i > n_grid - 3 and grid_v[i, j][0] > 0: grid_v[i, j][0] = 0
if j < 3 and grid_v[i, j][1] < 0: grid_v[i, j][1] = 0
if j > n_grid - 3 and grid_v[i, j][1] > 0: grid_v[i, j][1] = 0
for p in range(n_particles): # grid to particle (G2P)
base = (x[p] * inv_dx - 0.5).cast(int)
fx = x[p] * inv_dx - base.cast(float)
w = [0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1.0), 0.5 * ti.sqr(fx - 0.5)]
new_v = ti.Vector.zero(ti.f32, 2)
new_C = ti.Matrix.zero(ti.f32, 2, 2)
for i, j in ti.static(ti.ndrange(3, 3)): # loop over 3x3 grid node neighborhood
dpos = ti.Vector([i, j]).cast(float) - fx
g_v = grid_v[base + ti.Vector([i, j])]
weight = w[i][0] * w[j][1]
new_v += weight * g_v
new_C += 4 * inv_dx * weight * ti.outer_product(g_v, dpos)
v[p], C[p] = new_v, new_C
x[p] += dt * v[p] # advection
import random
group_size = n_particles // 3
for i in range(n_particles):
x[i] = [random.random() * 0.2 + 0.3 + 0.10 * (i // group_size), random.random() * 0.2 + 0.05 + 0.32 * (i // group_size)]
material[i] = i // group_size # 0: fluid 1: jelly 2: snow
v[i] = [0, 0]
F[i] = [[1, 0], [0, 1]]
Jp[i] = 1
import numpy as np
gui = ti.GUI("Taichi MLS-MPM-99", res=512, background_color=0x112F41)
for frame in range(20000):
for s in range(int(2e-3 // dt)):
substep()
colors = np.array([0x068587, 0xED553B, 0xEEEEF0], dtype=np.uint32)
gui.circles(x.to_numpy(), radius=1.5, color=colors[material.to_numpy()])
gui.show() # Change to gui.show(f'{frame:06d}.png') to write images to disk
2.3.3 利用python-taihci实现的其他demo
1.demo1:
-----fractal.py
import taichi as ti
n = 320
pixels = ti.var(dt=ti.f32, shape=(n * 2, n))
@ti.func
def complex_sqr(z):
return ti.Vector([z[0] * z[0] - z[1] * z[1], z[1] * z[0] * 2]) # z^2
@ti.kernel
def paint(t: ti.f32):
for i, j in pixels: # Parallized over all pixels
c = ti.Vector([-0.8, ti.cos(t) * 0.2])
z = ti.Vector([float(i) / n - 1, float(j) / n - 0.5]) * 2
iterations = 0
while z.norm() < 20 and iterations < 50:
z = complex_sqr(z) + c
iterations += 1
pixels[i, j] = 1 - iterations * 0.02
gui = ti.GUI("Julia Set", res=(n * 2, n))
for i in range(1000000):
paint(i * 0.03)
gui.set_image(pixels)
gui.show()
import taichi as ti
import os
real = ti.f32
dim = 2
n_particle_x = 100
n_particle_y = 8
n_particles = n_particle_x * n_particle_y
n_elements = (n_particle_x - 1) * (n_particle_y - 1) * 2
n_grid = 64
dx = 1 / n_grid
inv_dx = 1 / dx
dt = 1e-4
p_mass = 1
p_vol = 1
mu = 1
la = 1
scalar = lambda: ti.var(dt=real)
vec = lambda: ti.Vector(dim, dt=real)
mat = lambda: ti.Matrix(dim, dim, dt=real)
x, v, C = vec(), vec(), mat()
grid_v, grid_m = vec(), scalar()
restT = mat()
total_energy = scalar()
vertices = ti.var(ti.i32)
ti.cfg.arch = ti.cuda
@ti.layout
def place():
ti.root.dense(ti.k, n_particles).place(x, x.grad, v, C)
ti.root.dense(ti.ij, n_grid).place(grid_v, grid_m)
ti.root.dense(ti.i, n_elements).place(restT, restT.grad)
ti.root.dense(ti.ij, (n_elements, 3)).place(vertices)
ti.root.place(total_energy, total_energy.grad)
@ti.kernel
def clear_grid():
for i, j in grid_m:
grid_v[i, j] = [0, 0]
grid_m[i, j] = 0
@ti.func
def compute_T(i):
a = vertices[i, 0]
b = vertices[i, 1]
c = vertices[i, 2]
ab = x[b] - x[a]
ac = x[c] - x[a]
return ti.Matrix([[ab[0], ac[0]], [ab[1], ac[1]]])
@ti.kernel
def compute_rest_T():
for i in range(n_elements):
restT[i] = compute_T(i)
@ti.kernel
def compute_total_energy():
for i in range(n_elements):
currentT = compute_T(i)
F = currentT @ restT[i].inverse()
# NeoHookean
I1 = (F @ ti.Matrix.transposed(F)).trace()
J = ti.Matrix.determinant(F)
element_energy = 0.5 * mu * (
I1 - 2) - mu * ti.log(J) + 0.5 * la * ti.log(J)**2
ti.atomic_add(total_energy[None], element_energy * 1e-3)
@ti.kernel
def p2g():
for p in x:
base = ti.cast(x[p] * inv_dx - 0.5, ti.i32)
fx = x[p] * inv_dx - ti.cast(base, ti.f32)
w = [0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1), 0.5 * ti.sqr(fx - 0.5)]
affine = p_mass * C[p]
for i in ti.static(range(3)):
for j in ti.static(range(3)):
offset = ti.Vector([i, j])
dpos = (ti.cast(ti.Vector([i, j]), ti.f32) - fx) * dx
weight = w[i](0) * w[j](1)
grid_v[base + offset].atomic_add(
weight * (p_mass * v[p] - x.grad[p] + affine @ dpos))
grid_m[base + offset].atomic_add(weight * p_mass)
bound = 3
@ti.kernel
def grid_op():
for i, j in grid_m:
if grid_m[i, j] > 0:
inv_m = 1 / grid_m[i, j]
grid_v[i, j] = inv_m * grid_v[i, j]
grid_v(1)[i, j] -= dt * 9.8
# center sticky circle
if (i * dx - 0.5)**2 + (j * dx - 0.5)**2 < 0.005:
grid_v[i, j] = [0, 0]
# box
if i < bound and grid_v(0)[i, j] < 0:
grid_v(0)[i, j] = 0
if i > n_grid - bound and grid_v(0)[i, j] > 0:
grid_v(0)[i, j] = 0
if j < bound and grid_v(1)[i, j] < 0:
grid_v(1)[i, j] = 0
if j > n_grid - bound and grid_v(1)[i, j] > 0:
grid_v(1)[i, j] = 0
@ti.kernel
def g2p():
for p in x:
base = ti.cast(x[p] * inv_dx - 0.5, ti.i32)
fx = x[p] * inv_dx - ti.cast(base, ti.f32)
w = [
0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1.0), 0.5 * ti.sqr(fx - 0.5)
]
new_v = ti.Vector([0.0, 0.0])
new_C = ti.Matrix([[0.0, 0.0], [0.0, 0.0]])
for i in ti.static(range(3)):
for j in ti.static(range(3)):
dpos = ti.cast(ti.Vector([i, j]), ti.f32) - fx
g_v = grid_v[base(0) + i, base(1) + j]
weight = w[i](0) * w[j](1)
new_v += weight * g_v
new_C += 4 * weight * ti.outer_product(g_v, dpos) * inv_dx
v[p] = new_v
x[p] += dt * v[p]
C[p] = new_C
gui = ti.core.GUI("MPM", ti.veci(1024, 1024))
canvas = gui.get_canvas()
def mesh(i, j):
return i * n_particle_y + j
def main():
for i in range(n_particle_x):
for j in range(n_particle_y):
t = mesh(i, j)
x[t] = [0.1 + i * dx * 0.5, 0.7 + j * dx * 0.5]
v[t] = [0, -1]
# build mesh
for i in range(n_particle_x - 1):
for j in range(n_particle_y - 1):
# element id
eid = (i * (n_particle_y - 1) + j) * 2
vertices[eid, 0] = mesh(i, j)
vertices[eid, 1] = mesh(i + 1, j)
vertices[eid, 2] = mesh(i, j + 1)
eid = (i * (n_particle_y - 1) + j) * 2 + 1
vertices[eid, 0] = mesh(i, j + 1)
vertices[eid, 1] = mesh(i + 1, j + 1)
vertices[eid, 2] = mesh(i + 1, j)
compute_rest_T()
os.makedirs('tmp', exist_ok=True)
for f in range(600):
canvas.clear(0x112F41)
for s in range(50):
clear_grid()
# Note that we are now differentiating the total energy w.r.t. the particle position.
# Recall that F = - \partial (total_energy) / \partial x
with ti.Tape(total_energy):
# Do the forward computation of total energy and backward propagation for x.grad, which is later used in p2g
compute_total_energy()
# It's OK not to use the computed total_energy at all, since we only need x.grad
p2g()
grid_op()
g2p()
canvas.circle(ti.vec(0.5, 0.5)).radius(70).color(0x068587).finish()
# TODO: why is visualization so slow?
for i in range(n_elements):
for j in range(3):
a, b = vertices[i, j], vertices[i, (j + 1) % 3]
canvas.path(ti.vec(x[a][0], x[a][1]), ti.vec(
x[b][0], x[b][1])).radius(1).color(0x4FB99F).finish()
for i in range(n_particles):
canvas.circle(ti.vec(x[i][0], x[i][1])).radius(2).color(0xF2B134).finish()
gui.update()
gui.screenshot("tmp/{:04d}.png".format(f))
ti.profiler_print()
if __name__ == '__main__':
main()
import taichi as ti
import numpy as np
import math
ti.cfg.arch = ti.cuda # Try CUDA by default
screen_res = (800, 400)
screen_to_world_ratio = 10.0
boundary = (screen_res[0] / screen_to_world_ratio,
screen_res[1] / screen_to_world_ratio)
cell_size = 2.51
cell_recpr = 1.0 / cell_size
def round_up(f, s): return (math.floor(f * cell_recpr / s) + 1) * s
grid_size = (round_up(boundary[0], 1),
round_up(boundary[1], 1))
dim = 2
bg_color = 0x112f41
particle_color = 0x068587
boundary_color = 0xebaca2
num_particles_x = 60
num_particles = num_particles_x * 20
max_num_particles_per_cell = 100
max_num_neighbors = 100
time_delta = 1.0 / 20.0
epsilon = 1e-5
particle_radius = 3.0
particle_radius_in_world = particle_radius / screen_to_world_ratio
# PBF params
h = 1.1
mass = 1.0
rho0 = 1.0
lambda_epsilon = 100.0
pbf_num_iters = 5
corr_deltaQ_coeff = 0.3
corrK = 0.001
# Need ti.pow()
# corrN = 4.0
neighbor_radius = h * 1.05
poly6_factor = 315.0 / 64.0 / np.pi
spiky_grad_factor = -45.0 / np.pi
old_positions = ti.Vector(dim, dt=ti.f32)
positions = ti.Vector(dim, dt=ti.f32)
velocities = ti.Vector(dim, dt=ti.f32)
# Once taichi supports clear(), we can get rid of grid_num_particles
grid_num_particles = ti.var(ti.i32)
grid2particles = ti.var(ti.i32)
particle_num_neighbors = ti.var(ti.i32)
particle_neighbors = ti.var(ti.i32)
lambdas = ti.var(ti.f32)
position_deltas = ti.Vector(dim, dt=ti.f32)
# 0: x-pos, 1: timestep in sin()
board_states = ti.Vector(2, dt=ti.f32)
@ti.layout
def layout():
ti.root.dense(ti.i, num_particles).place(
old_positions, positions, velocities)
grid_snode = ti.root.dense(ti.ij, grid_size)
grid_snode.place(grid_num_particles)
grid_snode.dense(ti.k, max_num_particles_per_cell).place(grid2particles)
nb_node = ti.root.dense(ti.i, num_particles)
nb_node.place(particle_num_neighbors)
nb_node.dense(ti.j, max_num_neighbors).place(particle_neighbors)
ti.root.dense(ti.i, num_particles).place(lambdas, position_deltas)
ti.root.place(board_states)
@ti.func
def poly6_value(s, h):
result = 0.0
if 0 < s and s < h:
x = (h * h - s * s) / (h * h * h)
result = poly6_factor * x * x * x
return result
@ti.func
def spiky_gradient(r, h):
result = ti.Vector([0.0, 0.0])
r_len = r.norm()
if 0 < r_len and r_len < h:
x = (h - r_len) / (h * h * h)
g_factor = spiky_grad_factor * x * x
result = r * g_factor / r_len
return result
@ti.func
def compute_scorr(pos_ji):
# Eq (13)
x = poly6_value(pos_ji.norm(), h) / poly6_value(corr_deltaQ_coeff * h, h)
# pow(x, 4)
x = x * x
x = x * x
return (-corrK) * x
@ti.func
def get_cell(pos):
return (pos * cell_recpr).cast(int)
@ti.func
def is_in_grid(c):
# @c: Vector(i32)
return 0 <= c[0] and c[0] < grid_size[0] and 0 <= c[1] and c[1] < grid_size[1]
@ti.func
def confine_position_to_boundary(p):
bmin = particle_radius_in_world
bmax = ti.Vector([
board_states[None][0],
boundary[1]]) - particle_radius_in_world
for i in ti.static(range(dim)):
# Use randomness to prevent particles from sticking into each other after clamping
if p[i] <= bmin:
p[i] = bmin + epsilon * ti.random()
elif bmax[i] <= p[i]:
p[i] = bmax[i] - epsilon * ti.random()
return p
@ti.kernel
def blit_buffers(f: ti.template(), t: ti.template()):
for i in f:
t[i] = f[i]
@ti.kernel
def move_board():
# probably more accurate to exert force on particles according to hooke's law.
b = board_states[None]
b[1] += 1.0
period = 90
vel_strength = 8.0
if b[1] >= 2 * period:
b[1] = 0
b[0] += -ti.sin(b[1] * np.pi / period) * vel_strength * time_delta
board_states[None] = b
@ti.kernel
def apply_gravity_within_boundary():
for i in positions:
g = ti.Vector([0.0, -9.8])
pos, vel = positions[i], velocities[i]
vel += g * time_delta
pos += vel * time_delta
positions[i] = confine_position_to_boundary(pos)
@ti.kernel
def confine_to_boundary():
for i in positions:
pos = positions[i]
positions[i] = confine_position_to_boundary(pos)
@ti.kernel
def update_grid():
for p_i in positions:
cell = get_cell(positions[p_i])
# ti.Vector doesn't seem to support unpacking yet
# but we can directly use int Vectors as indices
offs = grid_num_particles[cell].atomic_add(1)
grid2particles[cell, offs] = p_i
@ti.kernel
def find_particle_neighbors():
for p_i in positions:
pos_i = positions[p_i]
cell = get_cell(pos_i)
nb_i = 0
for offs in ti.static(ti.grouped(ti.ndrange((-1, 2), (-1, 2)))):
cell_to_check = cell + offs
if is_in_grid(cell_to_check):
for j in range(grid_num_particles[cell_to_check]):
p_j = grid2particles[cell_to_check, j]
if nb_i < max_num_neighbors and p_j != p_i and (pos_i - positions[p_j]).norm() < neighbor_radius:
particle_neighbors[p_i, nb_i] = p_j
nb_i += 1
particle_num_neighbors[p_i] = nb_i
@ti.kernel
def compute_lambdas():
# Eq (8) ~ (11)
for p_i in positions:
pos_i = positions[p_i]
grad_i = ti.Vector([0.0, 0.0])
sum_gradient_sqr = 0.0
density_constraint = 0.0
for j in range(particle_num_neighbors[p_i]):
p_j = particle_neighbors[p_i, j]
# TODO: does taichi supports break?
if p_j >= 0:
pos_ji = pos_i - positions[p_j]
grad_j = spiky_gradient(pos_ji, h)
grad_i += grad_j
sum_gradient_sqr += grad_j.dot(grad_j)
# Eq(2)
density_constraint += poly6_value(pos_ji.norm(), h)
# Eq(1)
density_constraint = (mass * density_constraint / rho0) - 1.0
sum_gradient_sqr += grad_i.dot(grad_i)
lambdas[p_i] = (-density_constraint) / (sum_gradient_sqr + lambda_epsilon)
@ti.kernel
def compute_position_deltas():
# Eq(12), (14)
for p_i in positions:
pos_i = positions[p_i]
lambda_i = lambdas[p_i]
pos_delta_i = ti.Vector([0.0, 0.0])
for j in range(particle_num_neighbors[p_i]):
p_j = particle_neighbors[p_i, j]
# TODO: does taichi supports break?
if p_j >= 0:
lambda_j = lambdas[p_j]
pos_ji = pos_i - positions[p_j]
scorr_ij = compute_scorr(pos_ji)
pos_delta_i += (lambda_i + lambda_j + scorr_ij) * \
spiky_gradient(pos_ji, h)
pos_delta_i /= rho0
position_deltas[p_i] = pos_delta_i
@ti.kernel
def apply_position_deltas():
for i in positions:
positions[i] += position_deltas[i]
@ti.kernel
def update_velocities():
for i in positions:
velocities[i] = (positions[i] - old_positions[i]) / time_delta
def run_pbf():
blit_buffers(positions, old_positions)
apply_gravity_within_boundary()
grid_num_particles.fill(0)
particle_neighbors.fill(-1)
update_grid()
find_particle_neighbors()
for _ in range(pbf_num_iters):
compute_lambdas()
compute_position_deltas()
apply_position_deltas()
confine_to_boundary()
update_velocities()
# no vorticity/xsph because we cannot do cross product in 2D...
def render(gui, canvas):
canvas.clear(bg_color)
for pos in positions.to_numpy():
for j in range(dim):
pos[j] *= screen_to_world_ratio / screen_res[j]
canvas.circle(ti.vec(pos[0], pos[1])).radius(
particle_radius).color(particle_color).finish()
canvas.rect(ti.vec(0, 0), ti.vec(
board_states[None][0] / boundary[0], 1.0)).radius(1.5).color(boundary_color).close().finish()
gui.update()
def init_particles():
np_positions = np.zeros((num_particles, dim), dtype=np.float)
delta = h * 0.8
num_x = num_particles_x
num_y = num_particles // num_x
assert num_x * num_y == num_particles
offs = np.array([(boundary[0] - delta * num_x) * 0.5,
(boundary[1] * 0.02)])
for i in range(num_particles):
np_positions[i] = np.array([i % num_x, i // num_x]) * delta + offs
np_velocities = (np.random.rand(num_particles, dim).astype(
np.float) - 0.5) * 4.0
@ti.kernel
def init(p: ti.ext_arr(), v: ti.ext_arr()):
for i in range(num_particles):
for c in ti.static(range(dim)):
positions[i][c] = p[i, c]
velocities[i][c] = v[i, c]
@ti.kernel
def init2():
board_states[None] = ti.Vector([boundary[0] - epsilon, -0.0])
init(np_positions, np_velocities)
init2()
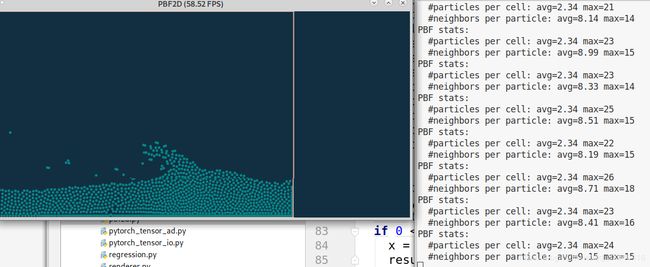
def print_stats():
print('PBF stats:')
num = grid_num_particles.to_numpy()
avg, max = np.mean(num), np.max(num)
print(f' #particles per cell: avg={avg:.2f} max={max}')
num = particle_num_neighbors.to_numpy()
avg, max = np.mean(num), np.max(num)
print(f' #neighbors per particle: avg={avg:.2f} max={max}')
def main():
init_particles()
print(f'boundary={boundary} grid={grid_size} cell_size={cell_size}')
gui = ti.core.GUI('PBF2D', ti.veci(screen_res[0], screen_res[1]))
canvas = gui.get_canvas()
print_counter = 0
while True:
move_board()
run_pbf()
print_counter += 1
if print_counter == 20:
print_stats()
print_counter = 0
render(gui, canvas)
if __name__ == '__main__':
main()
import taichi as ti
import taichi as tc
import matplotlib.pyplot as plt
import random
import numpy as np
tc.set_gdb_trigger(True)
number_coeffs = 4
learning_rate = 1e-4
N = 32
x, y = ti.var(ti.f32), ti.var(ti.f32)
coeffs = [ti.var(ti.f32) for _ in range(number_coeffs)]
loss = ti.var(ti.f32)
@ti.layout
def xy():
ti.root.dense(ti.i, N).place(x, x.grad, y, y.grad)
ti.root.place(loss, loss.grad)
for i in range(number_coeffs):
ti.root.place(coeffs[i], coeffs[i].grad)
@ti.kernel
def regress():
for i in x:
v = x[i]
est = 0.0
for j in ti.static(range(number_coeffs)):
est += coeffs[j] * ti.pow(v, j)
loss.atomic_add(0.5 * ti.sqr(y[i] - est))
@ti.kernel
def update():
for i in ti.static(range(number_coeffs)):
# ti.print(i)
# ti.print(coeffs[i][None])
# ti.print(coeffs[i].grad[None])
coeffs[i][None] -= learning_rate * coeffs[i].grad[None]
coeffs[i].grad[None] = 0
xs = []
ys = []
for i in range(N):
v = random.random() * 5 - 2.5
xs.append(v)
x[i] = v
y[i] = (v - 1) * (v - 2) * (v + 2) + random.random() - 0.5
regress()
print('y')
for i in range(N):
y.grad[i] = 1
ys.append(y[i])
print()
for i in range(1000):
loss[None] = 0
loss.grad[None] = 1
regress()
regress.grad()
print('Loss =', loss[None])
update()
for i in range(number_coeffs):
print(coeffs[i][None], end=', ')
print()
curve_xs = np.arange(-2.5, 2.5, 0.01)
curve_ys = curve_xs * 0
for i in range(number_coeffs):
curve_ys += coeffs[i][None] * np.power(curve_xs, i)
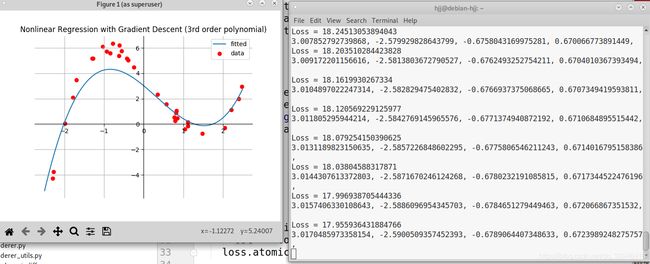
plt.title('Nonlinear Regression with Gradient Descent (3rd order polynomial)')
ax = plt.gca()
ax.scatter(xs, ys, label='data', color='r')
ax.plot(curve_xs, curve_ys, label='fitted')
ax.legend()
ax.grid(True)
ax.spines['left'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_position('zero')
ax.spines['top'].set_color('none')
plt.show()
import taichi as ti
import os
import numpy as np
import math
import time
import random
from renderer_utils import out_dir, ray_aabb_intersection, inf, eps, \
intersect_sphere, sphere_aabb_intersect_motion, inside_taichi
import sys
res = 1280, 720
num_spheres = 1024
color_buffer = ti.Vector(3, dt=ti.f32)
bbox = ti.Vector(3, dt=ti.f32)
grid_density = ti.var(dt=ti.i32)
voxel_has_particle = ti.var(dt=ti.i32)
max_ray_depth = 4
use_directional_light = True
particle_x = ti.Vector(3, dt=ti.f32)
particle_v = ti.Vector(3, dt=ti.f32)
particle_color = ti.Vector(3, dt=ti.f32)
pid = ti.var(ti.i32)
num_particles = ti.var(ti.i32)
fov = 0.23
dist_limit = 100
exposure = 1.5
camera_pos = ti.Vector([0.5, 0.32, 2.7])
vignette_strength = 0.9
vignette_radius = 0.0
vignette_center = [0.5, 0.5]
light_direction = [1.2, 0.3, 0.7]
light_direction_noise = 0.03
light_color = [1.0, 1.0, 1.0]
# ti.runtime.print_preprocessed = True
# ti.cfg.print_ir = True
ti.cfg.arch = ti.cuda
grid_visualization_block_size = 16
grid_resolution = 256 // grid_visualization_block_size
frame_id = 0
render_voxel = False
inv_dx = 256.0
dx = 1.0 / inv_dx
camera_pos = ti.Vector([0.5, 0.27, 2.7])
supporter = 2
shutter_time = 0.5e-3
sphere_radius = 0.0015
particle_grid_res = 256
max_num_particles_per_cell = 8192
max_num_particles = 1024 * 1024 * 4
assert sphere_radius * 2 * particle_grid_res < 1
@ti.layout
def buffers():
ti.root.dense(ti.ij, (res[0] // 8, res[1] // 8)).dense(ti.ij,
8).place(color_buffer)
ti.root.dense(ti.ijk, 2).dense(ti.ijk, particle_grid_res // 8).dense(
ti.ijk, 8).place(voxel_has_particle)
ti.root.dense(ti.ijk, 4).dense(
ti.ijk, particle_grid_res // 8).pointer().dense(ti.ijk, 8).dynamic(
ti.l, max_num_particles_per_cell, 128).place(pid)
ti.root.dense(ti.l, max_num_particles).place(particle_x, particle_v,
particle_color)
ti.root.place(num_particles)
ti.root.dense(ti.ijk, grid_resolution // 8).dense(ti.ijk,
8).place(grid_density)
ti.root.dense(ti.i, 2).place(bbox)
@ti.func
def inside_grid(ipos):
return ipos.min() >= 0 and ipos.max() < grid_resolution
# The dda algorithm requires the voxel grid to have one surrounding layer of void region
# to correctly render the outmost voxel faces
@ti.func
def inside_grid_loose(ipos):
return ipos.min() >= -1 and ipos.max() <= grid_resolution
@ti.func
def query_density_int(ipos):
inside = inside_grid(ipos)
ret = 0
if inside:
ret = grid_density[ipos]
else:
ret = 0
return ret
@ti.func
def voxel_color(pos):
p = pos * grid_resolution
p -= ti.Matrix.floor(p)
boundary = 0.1
count = 0
for i in ti.static(range(3)):
if p[i] < boundary or p[i] > 1 - boundary:
count += 1
f = 0.0
if count >= 2:
f = 1.0
return ti.Vector([0.2, 0.3, 0.2]) * (2.3 - 2 * f)
@ti.func
def sdf(o):
dist = 0.0
if ti.static(supporter == 0):
o -= ti.Vector([0.5, 0.002, 0.5])
p = o
h = 0.02
ra = 0.29
rb = 0.005
d = (ti.Vector([p[0], p[2]]).norm() - 2.0 * ra + rb, abs(p[1]) - h)
dist = min(max(d[0], d[1]), 0.0) + ti.Vector(
[max(d[0], 0.0), max(d[1], 0)]).norm() - rb
elif ti.static(supporter == 1):
o -= ti.Vector([0.5, 0.002, 0.5])
dist = (o.abs() - ti.Vector([0.5, 0.02, 0.5])).max()
else:
dist = o[1] - 0.027
return dist
@ti.func
def ray_march(p, d):
j = 0
dist = 0.0
limit = 200
while j < limit and sdf(p + dist * d) > 1e-8 and dist < dist_limit:
dist += sdf(p + dist * d)
j += 1
if dist > dist_limit:
dist = inf
return dist
@ti.func
def sdf_normal(p):
d = 1e-3
n = ti.Vector([0.0, 0.0, 0.0])
for i in ti.static(range(3)):
inc = p
dec = p
inc[i] += d
dec[i] -= d
n[i] = (0.5 / d) * (sdf(inc) - sdf(dec))
return ti.Matrix.normalized(n)
@ti.func
def sdf_color(p):
scale = 0.4
if inside_taichi(ti.Vector([p[0], p[2]])):
scale = 1
return ti.Vector([0.3, 0.5, 0.7]) * scale
@ti.func
def dda(eye_pos, d):
for i in ti.static(range(3)):
if abs(d[i]) < 1e-6:
d[i] = 1e-6
rinv = 1.0 / d
rsign = ti.Vector([0, 0, 0])
for i in ti.static(range(3)):
if d[i] > 0:
rsign[i] = 1
else:
rsign[i] = -1
bbox_min = ti.Vector([0.0, 0.0, 0.0]) - 10 * eps
bbox_max = ti.Vector([1.0, 1.0, 1.0]) + 10 * eps
inter, near, far = ray_aabb_intersection(bbox_min, bbox_max, eye_pos, d)
hit_distance = inf
normal = ti.Vector([0.0, 0.0, 0.0])
c = ti.Vector([0.0, 0.0, 0.0])
if inter:
near = max(0, near)
pos = eye_pos + d * (near + 5 * eps)
o = grid_resolution * pos
ipos = ti.Matrix.floor(o).cast(int)
dis = (ipos - o + 0.5 + rsign * 0.5) * rinv
running = 1
i = 0
hit_pos = ti.Vector([0.0, 0.0, 0.0])
while running:
last_sample = query_density_int(ipos)
if not inside_grid_loose(ipos):
running = 0
# normal = [0, 0, 0]
if last_sample:
mini = (ipos - o + ti.Vector([0.5, 0.5, 0.5]) - rsign * 0.5) * rinv
hit_distance = mini.max() * (1 / grid_resolution) + near
hit_pos = eye_pos + hit_distance * d
c = voxel_color(hit_pos)
running = 0
else:
mm = ti.Vector([0, 0, 0])
if dis[0] <= dis[1] and dis[0] < dis[2]:
mm[0] = 1
elif dis[1] <= dis[0] and dis[1] <= dis[2]:
mm[1] = 1
else:
mm[2] = 1
dis += mm * rsign * rinv
ipos += mm * rsign
normal = -mm * rsign
i += 1
return hit_distance, normal, c
@ti.func
def inside_particle_grid(ipos):
pos = ipos * dx
return bbox[0][0] <= pos[0] and pos[0] < bbox[1][0] and bbox[
0][1] <= pos[1] and pos[1] < bbox[1][1] and bbox[0][2] <= pos[2] and pos[2] < bbox[1][2]
@ti.func
def dda_particle(eye_pos, d, t):
grid_res = particle_grid_res
bbox_min = bbox[0]
bbox_max = bbox[1]
hit_pos = ti.Vector([0.0, 0.0, 0.0])
normal = ti.Vector([0.0, 0.0, 0.0])
c = ti.Vector([0.0, 0.0, 0.0])
for i in ti.static(range(3)):
if abs(d[i]) < 1e-6:
d[i] = 1e-6
inter, near, far = ray_aabb_intersection(bbox_min, bbox_max, eye_pos, d)
near = max(0, near)
closest_intersection = inf
if inter:
pos = eye_pos + d * (near + eps)
rinv = 1.0 / d
rsign = ti.Vector([0, 0, 0])
for i in ti.static(range(3)):
if d[i] > 0:
rsign[i] = 1
else:
rsign[i] = -1
o = grid_res * pos
ipos = ti.Matrix.floor(o).cast(int)
dis = (ipos - o + 0.5 + rsign * 0.5) * rinv
running = 1
while running:
inside = inside_particle_grid(ipos)
if inside:
num_particles = voxel_has_particle[ipos]
if num_particles != 0:
num_particles = ti.length(pid, ipos)
for k in range(num_particles):
p = pid[ipos[0], ipos[1], ipos[2], k]
v = particle_v[p]
x = particle_x[p] + t * v
color = particle_color[p]
dist, poss = intersect_sphere(eye_pos, d, x, sphere_radius)
hit_pos = poss
if dist < closest_intersection and dist > 0:
hit_pos = eye_pos + dist * d
closest_intersection = dist
normal = ti.Matrix.normalized(hit_pos - x)
c = color
else:
running = 0
normal = [0, 0, 0]
if closest_intersection < inf:
running = 0
else:
# hits nothing. Continue ray marching
mm = ti.Vector([0, 0, 0])
if dis[0] <= dis[1] and dis[0] <= dis[2]:
mm[0] = 1
elif dis[1] <= dis[0] and dis[1] <= dis[2]:
mm[1] = 1
else:
mm[2] = 1
dis += mm * rsign * rinv
ipos += mm * rsign
return closest_intersection, normal, c
@ti.func
def next_hit(pos, d, t):
closest = inf
normal = ti.Vector([0.0, 0.0, 0.0])
c = ti.Vector([0.0, 0.0, 0.0])
if ti.static(render_voxel):
closest, normal, c = dda(pos, d)
else:
closest, normal, c = dda_particle(pos, d, t)
if d[2] != 0:
ray_closest = -(pos[2] + 5.5) / d[2]
if ray_closest > 0 and ray_closest < closest:
closest = ray_closest
normal = ti.Vector([0.0, 0.0, 1.0])
c = ti.Vector([0.6, 0.7, 0.7])
ray_march_dist = ray_march(pos, d)
if ray_march_dist < dist_limit and ray_march_dist < closest:
closest = ray_march_dist
normal = sdf_normal(pos + d * closest)
c = sdf_color(pos + d * closest)
return closest, normal, c
aspect_ratio = res[0] / res[1]
@ti.kernel
def render():
ti.parallelize(6)
for u, v in color_buffer:
pos = camera_pos
d = ti.Vector([(
2 * fov * (u + ti.random(ti.f32)) / res[1] - fov * aspect_ratio - 1e-5),
2 * fov * (v + ti.random(ti.f32)) / res[1] - fov - 1e-5,
-1.0])
d = ti.Matrix.normalized(d)
t = (ti.random() - 0.5) * shutter_time
contrib = ti.Vector([0.0, 0.0, 0.0])
throughput = ti.Vector([1.0, 1.0, 1.0])
depth = 0
hit_sky = 1
ray_depth = 0
while depth < max_ray_depth:
closest, normal, c = next_hit(pos, d, t)
hit_pos = pos + closest * d
depth += 1
ray_depth = depth
if normal.norm() != 0:
d = out_dir(normal)
pos = hit_pos + 1e-4 * d
throughput *= c
if ti.static(use_directional_light):
dir_noise = ti.Vector(
[ti.random() - 0.5,
ti.random() - 0.5,
ti.random() - 0.5]) * light_direction_noise
direct = ti.Matrix.normalized(
ti.Vector(light_direction) + dir_noise)
dot = direct.dot(normal)
if dot > 0:
dist, _, _ = next_hit(pos, direct, t)
if dist > dist_limit:
contrib += throughput * ti.Vector(light_color) * dot
else: # hit sky
hit_sky = 1
depth = max_ray_depth
max_c = throughput.max()
if ti.random() > max_c:
depth = max_ray_depth
throughput = [0, 0, 0]
else:
throughput /= max_c
if hit_sky:
if ray_depth != 1:
# contrib *= max(d[1], 0.05)
pass
else:
# directly hit sky
pass
else:
throughput *= 0
# contrib += throughput
color_buffer[u, v] += contrib
support = 2
@ti.kernel
def initialize_particle_grid():
for p in particle_x:
if p < num_particles:
x = particle_x[p]
v = particle_v[p]
ipos = ti.Matrix.floor(x * particle_grid_res).cast(ti.i32)
for i in range(-support, support + 1):
for j in range(-support, support + 1):
for k in range(-support, support + 1):
offset = ti.Vector([i, j, k])
box_ipos = ipos + offset
if inside_particle_grid(box_ipos):
box_min = box_ipos * (1 / particle_grid_res)
box_max = (box_ipos + ti.Vector([1, 1, 1])) * (
1 / particle_grid_res)
if sphere_aabb_intersect_motion(
box_min, box_max, x - 0.5 * shutter_time * v,
x + 0.5 * shutter_time * v, sphere_radius):
ti.append(pid, box_ipos, p)
voxel_has_particle[box_ipos] = 1
@ti.kernel
def copy(img: ti.ext_arr()):
for i, j in color_buffer:
u = 1.0 * i / res[0]
v = 1.0 * j / res[1]
darken = 1.0 - vignette_strength * max((ti.sqrt(
ti.sqr(u - vignette_center[0]) + ti.sqr(v - vignette_center[1])) -
vignette_radius), 0)
for c in ti.static(range(3)):
img[i, j, c] = color_buffer[i, j][c] * darken
def main():
num_part = 100000
np_x = np.random.rand(num_part, 3).astype(np.float) * 0.4 + 0.2
np_v = np.random.rand(num_part, 3).astype(np.float) * 0
np_c = np.zeros((num_part, 3)).astype(np.float32)
np_c[:, 0] = 0.85
np_c[:, 1] = 0.9
np_c[:, 2] = 1
for i in range(3):
# bbox values must be multiples of dx
bbox[0][i] = (math.floor(np_x[:, i].min() * particle_grid_res) -
3.0) / particle_grid_res
bbox[1][i] = (math.floor(np_x[:, i].max() * particle_grid_res) +
3.0) / particle_grid_res
num_particles[None] = num_part
print('num_input_particles =', num_part)
@ti.kernel
def initialize_particle_x(x: ti.ext_arr(), v: ti.ext_arr(), color: ti.ext_arr()):
for i in range(max_num_particles):
if i < num_particles:
for c in ti.static(range(3)):
particle_x[i][c] = x[i, c]
particle_v[i][c] = v[i, c]
particle_color[i][c] = color[i, c]
# reconstruct grid using particle position and MPM p2g.
for k in ti.static(range(27)):
base_coord = (inv_dx * particle_x[i] - 0.5).cast(ti.i32) + ti.Vector(
[k // 9, k // 3 % 3, k % 3])
grid_density[base_coord // grid_visualization_block_size] = 1
initialize_particle_x(np_x, np_v, np_c)
initialize_particle_grid()
gui = ti.GUI('Particle Renderer', res)
last_t = 0
for i in range(500):
render()
interval = 10
if i % interval == 0:
img = np.zeros((res[0], res[1], 3), dtype=np.float32)
copy(img)
if last_t != 0:
print("time per spp = {:.2f} ms".format(
(time.time() - last_t) * 1000 / interval))
last_t = time.time()
img = img * (1 / (i + 1)) * exposure
img = np.sqrt(img)
gui.set_image(img)
gui.show()
if __name__ == '__main__':
main()
效果:
3 利用difftaichi编译环境实现物理模拟
3.1 difftaichi环境的特点
1.可微编程语言DiffTaichi,用于构建端到端可微程序。和目前常用的可微编程工具如TensorFlow、PyTorch相比,DiffTaichi更适合构建比常用操作(如卷积、BN等)更不规则的可微运算符,比如可微物理引擎中的粒子网格交互,网格采样等等。
2.DiffTachi的自动微分系统使用“两个尺度”设计:底层通过源代码变换保持并行性和算术强度(arithmetic intensity),上层通过一个轻量级的磁带(Tape)来记录大内核(Megakernel)的启动。
3.由于省去了枯燥的手动求导过程,DiffTaichi程序比CUDA短4.2倍并具有相同的性能;同时由于其Megakernel的设计,在编写复杂可微程序时,DiffTaichi比TensorFlow快188倍、比PyTorch快13.4倍。
3.2 使用difftaichi环境来进行物理模拟的demo
3.2.1
1.billiards.py
import taichi as ti
import sys
import math
import numpy as np
import os
import taichi as tc
import matplotlib.pyplot as plt
real = ti.f32
ti.set_default_fp(real)
max_steps = 2048
vis_interval = 64
output_vis_interval = 2
steps = 1024
assert steps * 2 <= max_steps
vis_resolution = 1024
scalar = lambda: ti.var(dt=real)
vec = lambda: ti.Vector(2, dt=real)
loss = scalar()
# ti.cfg.arch = ti.cuda
init_x = vec()
init_v = vec()
x = vec()
v = vec()
impulse = vec()
billiard_layers = 4
n_balls = 1 + (1 + billiard_layers) * billiard_layers // 2
target_ball = n_balls - 1
# target_ball = 0
goal = [0.9, 0.75]
radius = 0.03
elasticity = 0.8
@ti.layout
def place():
ti.root.dense(ti.l, max_steps).dense(ti.i, n_balls).place(x, v, impulse)
ti.root.place(init_x, init_v)
ti.root.place(loss)
ti.root.lazy_grad()
dt = 0.003
alpha = 0.00000
learning_rate = 0.01
@ti.kernel
def collide(t: ti.i32):
for i in range(n_balls):
for j in range(i):
imp = ti.Vector([0.0, 0.0])
if i != j:
dist = x[t, i] - x[t, j]
dist_norm = dist.norm()
if dist_norm < 2 * radius:
dir = ti.Vector.normalized(dist)
rela_v = v[t, i] - v[t, j]
projected_v = dir.dot(rela_v)
if projected_v < 0:
imp = -(1 + elasticity) * 0.5 * projected_v * dir
impulse[t + 1, i] += imp
for j_ in range(n_balls - i - 1):
j = j_ + i + 1
imp = ti.Vector([0.0, 0.0])
if i != j:
dist = x[t, i] - x[t, j]
dist_norm = dist.norm()
if dist_norm < 2 * radius:
dir = ti.Vector.normalized(dist)
rela_v = v[t, i] - v[t, j]
projected_v = dir.dot(rela_v)
if projected_v < 0:
imp = -(1 + elasticity) * 0.5 * projected_v * dir
impulse[t + 1, i] += imp
@ti.kernel
def advance(t: ti.i32):
for i in range(n_balls):
v[t, i] = v[t - 1, i] + impulse[t, i]
x[t, i] = x[t - 1, i] + dt * v[t, i]
@ti.kernel
def compute_loss(t: ti.i32):
loss[None] = ti.sqr(x[t, target_ball][0] -
goal[0]) + ti.sqr(x[t, target_ball][1] - goal[1])
@ti.kernel
def initialize():
x[0, 0] = init_x
v[0, 0] = init_v
gui = tc.core.GUI("Billiards", tc.veci(1024, 1024))
def forward(visualize=False, output=None):
initialize()
interval = vis_interval
if output:
interval = output_vis_interval
os.makedirs('billiards/{}/'.format(output), exist_ok=True)
count = 0
for i in range(billiard_layers):
for j in range(i + 1):
count += 1
x[0, count] = [
i * 2 * radius + 0.5, j * 2 * radius + 0.5 - i * radius * 0.7
]
pixel_radius = int(radius * 1024) + 1
canvas = gui.get_canvas()
for t in range(1, steps):
collide(t - 1)
advance(t)
if (t + 1) % interval == 0 and visualize:
canvas.clear(0x3C733F)
canvas.circle(tc.vec(goal[0], goal[1])).radius(
pixel_radius // 2).color(0x00000).finish()
for i in range(n_balls):
if i == 0:
color = 0xCCCCCC
elif i == n_balls - 1:
color = 0x3344cc
else:
color = 0xF20530
canvas.circle(tc.vec(
x[t, i][0], x[t, i][1])).radius(pixel_radius).color(color).finish()
gui.update()
if output:
gui.screenshot('billiards/{}/{:04d}.png'.format(output, t))
compute_loss(steps - 1)
@ti.kernel
def clear():
for t in range(0, max_steps):
for i in range(0, n_balls):
impulse[t, i] = ti.Vector([0.0, 0.0])
def optimize():
init_x[None] = [0.1, 0.5]
init_v[None] = [0.3, 0.0]
clear()
forward(visualize=True, output='initial')
for iter in range(200):
clear()
with ti.Tape(loss):
if iter % 20 == 0:
output = 'iter{:04d}'.format(iter)
else:
output = None
forward(visualize=True, output=output)
print('Iter=', iter, 'Loss=', loss[None])
for d in range(2):
init_x[None][d] -= learning_rate * init_x.grad[None][d]
init_v[None][d] -= learning_rate * init_v.grad[None][d]
clear()
forward(visualize=True, output='final')
def scan(zoom):
N = 1000
angles = []
losses = []
forward(visualize=True, output='initial')
for i in range(N):
alpha = ((i + 0.5) / N - 0.5) * math.pi * zoom
init_x[None] = [0.1, 0.5]
init_v[None] = [0.3 * math.cos(alpha), 0.3 * math.sin(alpha)]
loss[None] = 0
clear()
forward(visualize=False)
print(loss[None])
losses.append(loss[None])
angles.append(math.degrees(alpha))
plt.plot(angles, losses)
fig = plt.gcf()
fig.set_size_inches(5, 3)
plt.title('Billiard Scene Objective')
plt.ylabel('Objective')
plt.xlabel('Angle of velocity')
plt.tight_layout()
plt.show()
if __name__ == '__main__':
if len(sys.argv) > 1:
scan(float(sys.argv[1]))
else:
optimize()
import taichi as ti
import os
import math
import numpy as np
import matplotlib.pyplot as plt
import taichi as tc
real = ti.f32
ti.set_default_fp(real)
dim = 2
n_particles = 8192
n_solid_particles = 0
n_actuators = 0
n_grid = 128
dx = 1 / n_grid
inv_dx = 1 / dx
dt = 1e-3
p_vol = 1
E = 10
# TODO: update
mu = E
la = E
max_steps = 2048
steps = 1024
gravity = 3.8
target = [0.8, 0.2]
scalar = lambda: ti.var(dt=real)
vec = lambda: ti.Vector(dim, dt=real)
mat = lambda: ti.Matrix(dim, dim, dt=real)
actuator_id = ti.global_var(ti.i32)
particle_type = ti.global_var(ti.i32)
x, v = vec(), vec()
grid_v_in, grid_m_in = vec(), scalar()
grid_v_out = vec()
C, F = mat(), mat()
loss = scalar()
n_sin_waves = 4
weights = scalar()
bias = scalar()
x_avg = vec()
actuation = scalar()
actuation_omega = 20
act_strength = 4
# ti.cfg.arch = ti.cuda
@ti.layout
def place():
ti.root.dense(ti.ij, (n_actuators, n_sin_waves)).place(weights)
ti.root.dense(ti.i, n_actuators).place(bias)
ti.root.dense(ti.ij, (max_steps, n_actuators)).place(actuation)
ti.root.dense(ti.i, n_particles).place(actuator_id, particle_type)
ti.root.dense(ti.l, max_steps).dense(ti.k, n_particles).place(x, v, C, F)
ti.root.dense(ti.ij, n_grid).place(grid_v_in, grid_m_in, grid_v_out)
ti.root.place(loss, x_avg)
ti.root.lazy_grad()
@ti.kernel
def clear_grid():
for i, j in grid_m_in:
grid_v_in[i, j] = [0, 0]
grid_m_in[i, j] = 0
grid_v_in.grad[i, j] = [0, 0]
grid_m_in.grad[i, j] = 0
grid_v_out.grad[i, j] = [0, 0]
@ti.kernel
def clear_particle_grad():
# for all time steps and all particles
for f, i in x:
x.grad[f, i] = [0, 0]
v.grad[f, i] = [0, 0]
C.grad[f, i] = [[0, 0], [0, 0]]
F.grad[f, i] = [[0, 0], [0, 0]]
@ti.kernel
def clear_actuation_grad():
for t, i in actuation:
actuation[t, i] = 0.0
@ti.kernel
def p2g(f: ti.i32):
for p in range(0, n_particles):
base = ti.cast(x[f, p] * inv_dx - 0.5, ti.i32)
fx = x[f, p] * inv_dx - ti.cast(base, ti.i32)
w = [0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1), 0.5 * ti.sqr(fx - 0.5)]
new_F = (ti.Matrix.diag(dim=2, val=1) + dt * C[f, p]) @ F[f, p]
J = ti.determinant(new_F)
if particle_type[p] == 0: # fluid
sqrtJ = ti.sqrt(J)
new_F = ti.Matrix([[sqrtJ, 0], [0, sqrtJ]])
F[f + 1, p] = new_F
r, s = ti.polar_decompose(new_F)
act_id = actuator_id[p]
act = actuation[f, ti.max(0, act_id)] * act_strength
if act_id == -1:
act = 0.0
# ti.print(act)
A = ti.Matrix([[0.0, 0.0], [0.0, 1.0]]) * act
cauchy = ti.Matrix([[0.0, 0.0], [0.0, 0.0]])
mass = 0.0
if particle_type[p] == 0:
mass = 4
cauchy = ti.Matrix([[1.0, 0.0], [0.0, 0.1]]) * (J - 1) * E
else:
mass = 1
cauchy = 2 * mu * (new_F - r) @ ti.transposed(new_F) + \
ti.Matrix.diag(2, la * (J - 1) * J)
cauchy += new_F @ A @ ti.transposed(new_F)
stress = -(dt * p_vol * 4 * inv_dx * inv_dx) * cauchy
affine = stress + mass * C[f, p]
for i in ti.static(range(3)):
for j in ti.static(range(3)):
offset = ti.Vector([i, j])
dpos = (ti.cast(ti.Vector([i, j]), real) - fx) * dx
weight = w[i](0) * w[j](1)
grid_v_in[base + offset].atomic_add(
weight * (mass * v[f, p] + affine @ dpos))
grid_m_in[base + offset].atomic_add(weight * mass)
bound = 3
coeff = 0.5
@ti.kernel
def grid_op():
for i, j in grid_m_in:
inv_m = 1 / (grid_m_in[i, j] + 1e-10)
v_out = inv_m * grid_v_in[i, j]
v_out[1] -= dt * gravity
if i < bound and v_out[0] < 0:
v_out[0] = 0
v_out[1] = 0
if i > n_grid - bound and v_out[0] > 0:
v_out[0] = 0
v_out[1] = 0
if j < bound and v_out[1] < 0:
v_out[0] = 0
v_out[1] = 0
normal = ti.Vector([0.0, 1.0])
lsq = ti.sqr(normal).sum()
if lsq > 0.5:
if ti.static(coeff < 0):
v_out(0).val = 0
v_out(1).val = 0
else:
lin = (ti.transposed(v_out) @ normal)(0)
if lin < 0:
vit = v_out - lin * normal
lit = vit.norm() + 1e-10
if lit + coeff * lin <= 0:
v_out(0).val = 0
v_out(1).val = 0
else:
v_out = (1 + coeff * lin / lit) * vit
if j > n_grid - bound and v_out[1] > 0:
v_out[0] = 0
v_out[1] = 0
grid_v_out[i, j] = v_out
@ti.kernel
def g2p(f: ti.i32):
for p in range(0, n_particles):
base = ti.cast(x[f, p] * inv_dx - 0.5, ti.i32)
fx = x[f, p] * inv_dx - ti.cast(base, real)
w = [
0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1.0), 0.5 * ti.sqr(fx - 0.5)
]
new_v = ti.Vector([0.0, 0.0])
new_C = ti.Matrix([[0.0, 0.0], [0.0, 0.0]])
for i in ti.static(range(3)):
for j in ti.static(range(3)):
dpos = ti.cast(ti.Vector([i, j]), real) - fx
g_v = grid_v_out[base(0) + i, base(1) + j]
weight = w[i](0) * w[j](1)
new_v += weight * g_v
new_C += 4 * weight * ti.outer_product(g_v, dpos) * inv_dx
v[f + 1, p] = new_v
x[f + 1, p] = x[f, p] + dt * v[f + 1, p]
C[f + 1, p] = new_C
@ti.kernel
def compute_actuation(t: ti.i32):
for i in range(n_actuators):
act = 0.0
for j in ti.static(range(n_sin_waves)):
act += weights[i, j] * ti.sin(actuation_omega * t * dt +
2 * math.pi / n_sin_waves * j)
act += bias[i]
actuation[t, i] = ti.tanh(act)
@ti.kernel
def compute_x_avg():
for i in range(n_particles):
contrib = 0.0
if particle_type[i] == 1:
contrib = 1.0 / n_solid_particles
x_avg[None].atomic_add(contrib * x[steps - 1, i])
@ti.kernel
def compute_loss():
dist = x_avg[None][0]
loss[None] = -dist
@ti.complex_kernel
def advance(s):
clear_grid()
compute_actuation(s)
p2g(s)
grid_op()
g2p(s)
@ti.complex_kernel_grad(advance)
def advance_grad(s):
clear_grid()
p2g(s)
grid_op()
g2p.grad(s)
grid_op.grad()
p2g.grad(s)
compute_actuation.grad(s)
def forward(total_steps=steps):
# simulation
for s in range(total_steps - 1):
advance(s)
x_avg[None] = [0, 0]
compute_x_avg()
compute_loss()
class Scene:
def __init__(self):
self.n_particles = 0
self.n_solid_particles = 0
self.x = []
self.actuator_id = []
self.particle_type = []
self.offset_x = 0
self.offset_y = 0
def add_rect(self, x, y, w, h, actuation, ptype=1):
if ptype == 0:
assert actuation == -1
global n_particles
w_count = int(w / dx) * 2
h_count = int(h / dx) * 2
real_dx = w / w_count
real_dy = h / h_count
for i in range(w_count):
for j in range(h_count):
self.x.append([
x + (i + 0.5) * real_dx + self.offset_x,
y + (j + 0.5) * real_dy + self.offset_y
])
self.actuator_id.append(actuation)
self.particle_type.append(ptype)
self.n_particles += 1
self.n_solid_particles += int(ptype == 1)
def set_offset(self, x, y):
self.offset_x = x
self.offset_y = y
def finalize(self):
global n_particles, n_solid_particles
n_particles = self.n_particles
n_solid_particles = self.n_solid_particles
print('n_particles', n_particles)
print('n_solid', n_solid_particles)
def set_n_actuators(self, n_act):
global n_actuators
n_actuators = n_act
def fish(scene):
scene.add_rect(0.025, 0.025, 0.95, 0.1, -1, ptype=0)
scene.add_rect(0.1, 0.2, 0.15, 0.05, -1)
scene.add_rect(0.1, 0.15, 0.025, 0.05, 0)
scene.add_rect(0.125, 0.15, 0.025, 0.05, 1)
scene.add_rect(0.2, 0.15, 0.025, 0.05, 2)
scene.add_rect(0.225, 0.15, 0.025, 0.05, 3)
scene.set_n_actuators(4)
def robot(scene):
scene.set_offset(0.1, 0.03)
scene.add_rect(0.0, 0.1, 0.3, 0.1, -1)
scene.add_rect(0.0, 0.0, 0.05, 0.1, 0)
scene.add_rect(0.05, 0.0, 0.05, 0.1, 1)
scene.add_rect(0.2, 0.0, 0.05, 0.1, 2)
scene.add_rect(0.25, 0.0, 0.05, 0.1, 3)
scene.set_n_actuators(4)
from renderer_vector import rgb_to_hex
gui = tc.core.GUI("Differentiable MPM", tc.veci(1024, 1024))
canvas = gui.get_canvas()
def visualize(s, folder):
canvas.clear(0xFFFFFF)
vec = tc.vec
for i in range(n_particles):
color = 0x111111
aid = actuator_id[i]
if aid != -1:
act = actuation[s - 1, aid]
color = rgb_to_hex((0.5 - act, 0.5 - abs(act), 0.5 + act))
canvas.circle(vec(x[s, i][0], x[s, i][1])).radius(2).color(color).finish()
canvas.path(tc.vec(0.05, 0.02), tc.vec(0.95,
0.02)).radius(3).color(0x0).finish()
gui.update()
os.makedirs(folder, exist_ok=True)
gui.screenshot('{}/{:04d}.png'.format(folder, s))
def main():
tc.set_gdb_trigger()
# initialization
scene = Scene()
# fish(scene)
robot(scene)
scene.finalize()
for i in range(n_actuators):
for j in range(n_sin_waves):
weights[i, j] = np.random.randn() * 0.01
for i in range(scene.n_particles):
x[0, i] = scene.x[i]
F[0, i] = [[1, 0], [0, 1]]
actuator_id[i] = scene.actuator_id[i]
particle_type[i] = scene.particle_type[i]
losses = []
for iter in range(100):
with ti.Tape(loss):
forward()
l = loss[None]
losses.append(l)
print('i=', iter, 'loss=', l)
learning_rate = 0.1
for i in range(n_actuators):
for j in range(n_sin_waves):
# print(weights.grad[i, j])
weights[i, j] -= learning_rate * weights.grad[i, j]
bias[i] -= learning_rate * bias.grad[i]
if iter % 10 == 9:
# visualize
forward(1500)
for s in range(63, 1500, 16):
visualize(s, 'diffmpm/iter{:03d}/'.format(iter))
# ti.profiler_print()
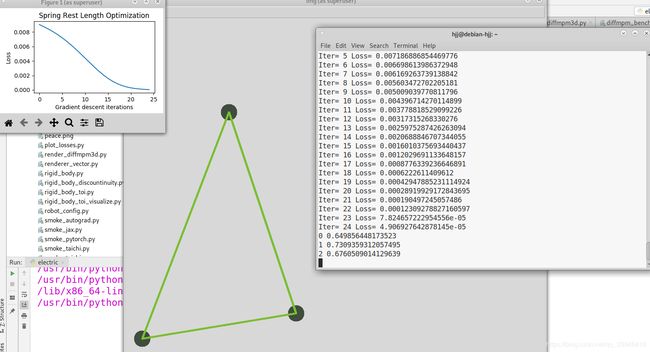
plt.title("Optimization of Initial Velocity")
plt.ylabel("Loss")
plt.xlabel("Gradient Descent Iterations")
plt.plot(losses)
plt.show()
if __name__ == '__main__':
main()
import taichi as ti
import numpy as np
import cv2
import matplotlib.pyplot as plt
import time
real = ti.f32
ti.set_default_fp(real)
ti.cfg.enable_profiler = False
# ti.cfg.use_llvm = True
dim = 2
n_particles = 6400
N = 80
n_grid = 120
dx = 1 / n_grid
inv_dx = 1 / dx
dt = 3e-4
p_mass = 1
p_vol = 1
E = 100
# TODO: update
mu = E
la = E
max_steps = 1024
steps = 1024
gravity = 9.8
target = [0.3, 0.6]
scalar = lambda: ti.var(dt=real)
vec = lambda: ti.Vector(dim, dt=real)
mat = lambda: ti.Matrix(dim, dim, dt=real)
x, v, x_avg = vec(), vec(), vec()
grid_v_in, grid_m_in = vec(), scalar()
grid_v_out = vec()
C, F = mat(), mat()
init_v = vec()
loss = scalar()
ti.cfg.arch = ti.cuda
@ti.layout
def place():
def p(x):
for i in x.entries:
ti.root.dense(ti.l, max_steps).dense(ti.k, n_particles).place(i)
ti.root.dense(ti.l, max_steps).dense(ti.k, n_particles).place(i.grad)
# ti.root.dense(ti.l, max_steps).dense(ti.k, n_particles).place(x, v, C, F)
p(x)
p(v)
p(C)
p(F)
def pg(x):
# ti.root.dense(ti.ij, n_grid // 8).dense(ti.ij, 8).place(x)
ti.root.dense(ti.ij, n_grid).place(x)
def pgv(x):
for i in x.entries:
ti.root.dense(ti.ij, n_grid).place(i)
pgv(grid_v_in)
pg(grid_m_in)
pg(grid_v_out)
# ti.root.dense(ti.ij, n_grid).place(grid_v_in, grid_m_in, grid_v_out)
# ti.root.dense(ti.ij, n_grid).place(grid_v_in, grid_m_in, grid_v_out)
ti.root.place(init_v, loss, x_avg)
ti.root.lazy_grad()
@ti.kernel
def set_v():
for i in range(n_particles):
v[0, i] = init_v
@ti.kernel
def clear_grid():
for i, j in grid_m_in:
grid_v_in[i, j] = [0, 0]
grid_m_in[i, j] = 0
grid_v_in.grad[i, j] = [0, 0]
grid_m_in.grad[i, j] = 0
grid_v_out.grad[i, j] = [0, 0]
@ti.kernel
def p2g(f: ti.i32):
for p in range(0, n_particles):
base = ti.cast(x[f, p] * inv_dx - 0.5, ti.i32)
fx = x[f, p] * inv_dx - ti.cast(base, ti.i32)
w = [0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1), 0.5 * ti.sqr(fx - 0.5)]
new_F = (ti.Matrix.diag(dim=2, val=1) + dt * C[f, p]) @ F[f, p]
F[f + 1, p] = new_F
J = ti.determinant(new_F)
r, s = ti.polar_decompose(new_F)
cauchy = 2 * mu * (new_F - r) @ ti.transposed(new_F) + \
ti.Matrix.diag(2, la * (J - 1) * J)
stress = -(dt * p_vol * 4 * inv_dx * inv_dx) * cauchy
affine = stress + p_mass * C[f, p]
for i in ti.static(range(3)):
for j in ti.static(range(3)):
offset = ti.Vector([i, j])
dpos = (ti.cast(ti.Vector([i, j]), real) - fx) * dx
weight = w[i](0) * w[j](1)
grid_v_in[base + offset].atomic_add(
weight * (p_mass * v[f, p] + affine @ dpos))
grid_m_in[base + offset].atomic_add(weight * p_mass)
bound = 3
@ti.kernel
def grid_op():
for p in range(n_grid * n_grid):
i = p // n_grid
j = p - n_grid * i
inv_m = 1 / (grid_m_in[i, j] + 1e-10)
v_out = inv_m * grid_v_in[i, j]
v_out[1] -= dt * gravity
if i < bound and v_out[0] < 0:
v_out[0] = 0
if i > n_grid - bound and v_out[0] > 0:
v_out[0] = 0
if j < bound and v_out[1] < 0:
v_out[1] = 0
if j > n_grid - bound and v_out[1] > 0:
v_out[1] = 0
grid_v_out[i, j] = v_out
@ti.kernel
def g2p(f: ti.i32):
for p in range(n_particles):
base = ti.cast(x[f, p] * inv_dx - 0.5, ti.i32)
fx = x[f, p] * inv_dx - ti.cast(base, real)
w = [
0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1.0), 0.5 * ti.sqr(fx - 0.5)
]
new_v = ti.Vector([0.0, 0.0])
new_C = ti.Matrix([[0.0, 0.0], [0.0, 0.0]])
for i in ti.static(range(3)):
for j in ti.static(range(3)):
dpos = ti.cast(ti.Vector([i, j]), real) - fx
g_v = grid_v_out[base(0) + i, base(1) + j]
weight = w[i](0) * w[j](1)
new_v += weight * g_v
new_C += 4 * weight * ti.outer_product(g_v, dpos) * inv_dx
v[f + 1, p] = new_v
x[f + 1, p] = x[f, p] + dt * v[f + 1, p]
C[f + 1, p] = new_C
@ti.kernel
def compute_x_avg():
for i in range(n_particles):
x_avg[None].atomic_add((1 / n_particles) * x[steps - 1, i])
@ti.kernel
def compute_loss():
dist = ti.sqr(x_avg - ti.Vector(target))
loss[None] = 0.5 * (dist(0) + dist(1))
@ti.complex_kernel
def substep(s):
clear_grid()
p2g(s)
grid_op()
g2p(s)
@ti.complex_kernel_grad(substep)
def substep_grad(s):
clear_grid()
p2g(s)
grid_op()
g2p.grad(s)
grid_op.grad()
p2g.grad(s)
def benchmark():
print(
'Also check "nvprof --print-gpu-trace python3 diffmpm_benchmark.py" for more accurate results'
)
iters = 100000
for i in range(1):
p2g(0)
grid_op()
g2p(0)
t = time.time()
ti.runtime.sync()
for i in range(iters):
# clear_grid()
p2g(0)
grid_op()
g2p(0)
ti.runtime.sync()
print('forward ', (time.time() - t) / iters * 1000 * 3, 'ms')
ti.profiler_print()
for i in range(1):
p2g.grad(0)
grid_op.grad()
g2p.grad(0)
t = time.time()
ti.runtime.sync()
for i in range(iters):
# clear_grid()
g2p.grad(0)
grid_op.grad()
p2g.grad(0)
ti.runtime.sync()
print('backward ', (time.time() - t) / iters * 1000 * 3, 'ms')
ti.profiler_print()
def main():
# initialization
init_v[None] = [0, 0]
for i in range(n_particles):
F[0, i] = [[1, 0], [0, 1]]
for i in range(N):
for j in range(N):
x[0, i * N + j] = [dx * (i * 0.5 + 10), dx * (j * 0.5 + 25)]
set_v()
benchmark()
losses = []
img_count = 0
for i in range(30):
with ti.Tape(loss=loss):
set_v()
for s in range(steps - 1):
substep(s)
loss[None] = 0
x_avg[None] = [0, 0]
compute_x_avg()
compute_loss()
l = loss[None]
losses.append(l)
grad = init_v.grad[None]
print('loss=', l, ' grad=', (grad[0], grad[1]))
learning_rate = 10
init_v(0)[None] -= learning_rate * grad[0]
init_v(1)[None] -= learning_rate * grad[1]
# visualize
for s in range(63, steps, 64):
scale = 4
img = np.zeros(shape=(scale * n_grid, scale * n_grid)) + 0.3
total = [0, 0]
for i in range(n_particles):
p_x = int(scale * x(0)[s, i] / dx)
p_y = int(scale * x(1)[s, i] / dx)
total[0] += p_x
total[1] += p_y
img[p_x, p_y] = 1
cv2.circle(
img, (total[1] // n_particles, total[0] // n_particles),
radius=5,
color=0,
thickness=5)
cv2.circle(
img,
(int(target[1] * scale * n_grid), int(target[0] * scale * n_grid)),
radius=5,
color=1,
thickness=5)
img = img.swapaxes(0, 1)[::-1]
cv2.imshow('MPM', img)
img_count += 1
# cv2.imwrite('MPM{:04d}.png'.format(img_count), img * 255)
cv2.waitKey(1)
ti.profiler_print()
ti.profiler_print()
plt.title("Optimization of Initial Velocity")
plt.ylabel("Loss")
plt.xlabel("Gradient Descent Iterations")
plt.plot(losses)
plt.show()
if __name__ == '__main__':
main()
import taichi as ti
import random
import sys
import math
import numpy as np
import os
import taichi as tc
import matplotlib.pyplot as plt
real = ti.f32
ti.set_default_fp(real)
max_steps = 2048
vis_interval = 8
output_vis_interval = 8
steps = 512
seg_size = 256
vis_resolution = 1024
scalar = lambda: ti.var(dt=real)
vec = lambda: ti.Vector(2, dt=real)
loss = scalar()
hidden = scalar()
damping = 0.2
x = vec()
v = vec()
n_gravitation = 8
goal = vec()
goal_v = vec()
gravitation = scalar()
n_hidden = 64
weight1 = scalar()
bias1 = scalar()
weight2 = scalar()
bias2 = scalar()
pad = 0.1
gravitation_position = [[pad, pad], [pad, 1 - pad], [1 - pad, 1 - pad],
[1 - pad, pad], [0.5, 1 - pad], [0.5, pad], [pad, 0.5],
[1 - pad, 0.5]]
@ti.layout
def place():
ti.root.dense(ti.l, max_steps).place(x, v)
ti.root.dense(ti.l, max_steps).dense(ti.i, n_hidden).place(hidden)
ti.root.dense(ti.l, max_steps).dense(ti.i, n_gravitation).place(gravitation)
ti.root.dense(ti.ij, (8, n_hidden)).place(weight1)
ti.root.dense(ti.i, n_hidden).place(bias1)
ti.root.dense(ti.ij, (n_hidden, n_gravitation)).place(weight2)
ti.root.dense(ti.i, n_gravitation).place(bias2)
ti.root.place(loss)
ti.root.dense(ti.i, max_steps).place(goal, goal_v)
ti.root.lazy_grad()
dt = 0.03
alpha = 0.00000
learning_rate = 2e-2
K = 1e-3
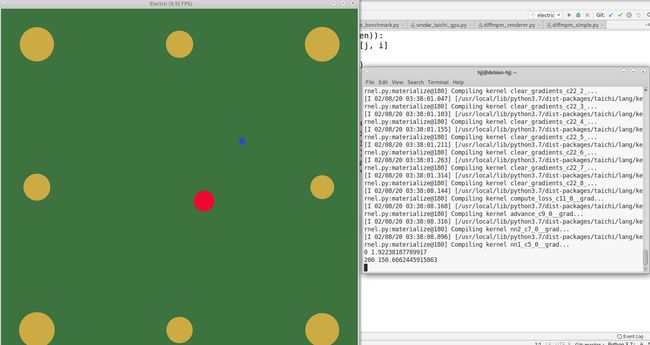
@ti.kernel
def nn1(t: ti.i32):
for i in range(n_hidden):
act = 0.0
act += (x[t][0] - 0.5) * weight1[0, i]
act += (x[t][1] - 0.5) * weight1[1, i]
act += v[t][0] * weight1[2, i]
act += v[t][1] * weight1[3, i]
act += (goal[t][0] - 0.5) * weight1[4, i]
act += (goal[t][1] - 0.5) * weight1[5, i]
act += (goal_v[t][0] - 0.5) * weight1[6, i]
act += (goal_v[t][1] - 0.5) * weight1[7, i]
act += bias1[i]
hidden[t, i] = ti.tanh(act)
@ti.kernel
def nn2(t: ti.i32):
for i in range(n_gravitation):
act = 0.0
for j in ti.static(range(n_hidden)):
act += hidden[t, j] * weight2[j, i]
act += bias2[i]
gravitation[t, i] = ti.tanh(act)
@ti.kernel
def advance(t: ti.i32):
for _ in range(1): # parallelize this loop
gravitational_force = ti.Vector([0.0, 0.0])
for i in ti.static(range(n_gravitation)): # instead of this one
r = x[t - 1] - ti.Vector(gravitation_position[i])
len_r = ti.max(r.norm(), 1e-1)
gravitational_force += K * gravitation[t, i] / (len_r * len_r * len_r) * r
v[t] = v[t - 1] * math.exp(-dt * damping) + dt * gravitational_force
x[t] = x[t - 1] + dt * v[t]
@ti.kernel
def compute_loss(t: ti.i32):
ti.atomic_add(loss[None], dt * (x[t] - goal[t]).norm_sqr())
gui = tc.core.GUI("Electric", tc.veci(1024, 1024))
def forward(visualize=False, output=None):
interval = vis_interval
if output:
interval = output_vis_interval
os.makedirs('electric/{}/'.format(output), exist_ok=True)
canvas = gui.get_canvas()
for t in range(1, steps):
nn1(t)
nn2(t)
advance(t)
compute_loss(t)
if (t + 1) % interval == 0 and visualize:
canvas.clear(0x3C733F)
for i in range(n_gravitation):
r = (gravitation[t, i] + 1) * 30
canvas.circle(tc.vec(*gravitation_position[i])).radius(r).color(
0xccaa44).finish()
canvas.circle(tc.vec(x[t][0],
x[t][1])).radius(30).color(0xF20530).finish()
canvas.circle(tc.vec(goal[t][0],
goal[t][1])).radius(10).color(0x3344cc).finish()
gui.update()
if output:
gui.screenshot('electric/{}/{:04d}.png'.format(output, t))
def rand():
return 0.2 + random.random() * 0.6
tasks = [((rand(), rand()), (rand(), rand())) for i in range(10)]
def lerp(x, a, b):
return (1 - x) * a + x * b
def initialize():
# x[0] = [rand(), rand()]
segments = steps // seg_size
points = []
for i in range(segments + 1):
points.append([rand(), rand()])
for i in range(segments):
for j in range(steps // segments):
k = steps // segments * i + j
goal[k] = [
lerp(j / seg_size, points[i][0], points[i + 1][0]),
lerp(j / seg_size, points[i][1], points[i + 1][1])
]
goal_v[k] = [
points[i + 1][0] - points[i][0], points[i + 1][1] - points[i][1]
]
x[0] = points[0]
# x[0] = [0.3, 0.6]
# goal[None] = [0.5, 0.2]
# i = random.randrange(2)
# x[0] = tasks[i][0]
# goal[None] = tasks[i][1]
def optimize():
initialize()
forward(visualize=True, output='initial')
losses = []
for iter in range(200000):
initialize()
vis = iter % 200 == 0
output = None
if vis:
output = 'iter{:05d}'.format(iter)
with ti.Tape(loss):
forward(visualize=vis, output=output)
losses.append(loss[None])
# print(iter, "loss", loss[None])
if vis:
print(iter, sum(losses))
losses.clear()
tot = 0
for i in range(8):
for j in range(n_hidden):
weight1[i, j] = weight1[i, j] - weight1.grad[i, j] * learning_rate
tot += weight1.grad[i, j]**2
# print(tot)
for j in range(n_hidden):
bias1[j] = bias1[j] - bias1.grad[j] * learning_rate
for i in range(n_hidden):
for j in range(n_gravitation):
weight2[i, j] = weight2[i, j] - weight2.grad[i, j] * learning_rate
for j in range(n_gravitation):
bias2[j] = bias2[j] - bias2.grad[j] * learning_rate
forward(visualize=True, output='final')
if __name__ == '__main__':
for i in range(8):
for j in range(n_hidden):
weight1[i, j] = (random.random() - 0.5) * 0.3
for i in range(n_hidden):
for j in range(n_gravitation):
weight2[i, j] = (random.random() - 0.5) * 0.3
optimize()
import taichi as ti
import math
import numpy as np
import cv2
import os
import matplotlib.pyplot as plt
real = ti.f32
ti.set_default_fp(real)
max_steps = 1024
vis_interval = 256
output_vis_interval = 8
steps = 1024
vis_resolution = 1024
n_objects = 3
mass = 1
n_springs = 3
spring_stiffness = 10
damping = 20
scalar = lambda: ti.var(dt=real)
vec = lambda: ti.Vector(2, dt=real)
loss = scalar()
x = vec()
v = vec()
force = vec()
spring_anchor_a = ti.global_var(ti.i32)
spring_anchor_b = ti.global_var(ti.i32)
spring_length = scalar()
@ti.layout
def place():
ti.root.dense(ti.l, max_steps).dense(ti.i, n_objects).place(x, v, force)
ti.root.dense(ti.i, n_springs).place(spring_anchor_a, spring_anchor_b,
spring_length)
ti.root.place(loss)
ti.root.lazy_grad()
dt = 0.001
learning_rate = 5
@ti.kernel
def apply_spring_force(t: ti.i32):
# Kernels can have parameters. there t is a parameter with type int32.
for i in range(n_springs): # A parallel for, preferably on GPUs
a, b = spring_anchor_a[i], spring_anchor_b[i]
x_a, x_b = x[t - 1, a], x[t - 1, b]
dist = x_a - x_b
length = dist.norm() + 1e-4
F = (length - spring_length[i]) * spring_stiffness * dist / length
# apply spring impulses to mass points. Use atomic_add for parallel safety.
ti.atomic_add(force[t, a], -F)
ti.atomic_add(force[t, b], F)
friction = 0.01
@ti.kernel
def time_integrate(t: ti.i32):
for i in range(n_objects):
s = math.exp(-dt * damping)
new_v = s * v[t - 1, i] + dt * force[t, i] / mass
new_x = x[t - 1, i] + dt * new_v
if new_x[0] > 0.4 and new_v[0] > 0:
# friction projection
if new_v[1] > 0:
new_v[1] -= ti.min(new_v[1], friction * new_v[0])
if new_v[1] < 0:
new_v[1] += ti.min(-new_v[1], friction * new_v[0])
new_v[0] = 0
v[t, i] = new_v
x[t, i] = new_x
@ti.kernel
def compute_loss(t: ti.i32):
x01 = x[t, 0] - x[t, 1]
x02 = x[t, 0] - x[t, 2]
area = ti.abs(
0.5 * (x01[0] * x02[1] - x01[1] * x02[0])) # area from cross product
target_area = 0.1
loss[None] = ti.sqr(area - target_area)
def visualize(output, t):
img = np.ones(
shape=(vis_resolution, vis_resolution, 3),
dtype=np.float32) * (216 / 255.0)
def circle(x, y, color):
radius = 0.02
cv2.circle(
img,
center=(int(vis_resolution * x), int(vis_resolution * (1 - y))),
radius=int(radius * vis_resolution),
color=color,
thickness=-1)
for i in range(n_objects):
color = (0.24, 0.3, 0.25)
circle(x[t, i][0], x[t, i][1], color)
for i in range(n_springs):
def get_pt(x):
return int(
x[0] * vis_resolution), int(vis_resolution - x[1] * vis_resolution)
cv2.line(
img,
get_pt(x[t, spring_anchor_a[i]]),
get_pt(x[t, spring_anchor_b[i]]), (0.2, 0.75, 0.48),
thickness=4)
cv2.imshow('img', img)
cv2.waitKey(1)
if output:
cv2.imwrite('mass_spring_simple/{}/{:04d}.png'.format(output, t), img * 255)
def forward(output=None):
interval = vis_interval
if output:
interval = output_vis_interval
os.makedirs('mass_spring_simple/{}/'.format(output), exist_ok=True)
for t in range(1, steps):
apply_spring_force(t)
time_integrate(t)
if (t + 1) % interval == 0:
visualize(output, t)
compute_loss(steps - 1)
@ti.kernel
def clear_states():
for t in range(0, max_steps):
for i in range(0, n_objects):
x.grad[t, i] = ti.Vector([0.0, 0.0])
v.grad[t, i] = ti.Vector([0.0, 0.0])
force[t, i] = ti.Vector([0.0, 0.0])
force.grad[t, i] = ti.Vector([0.0, 0.0])
@ti.kernel
def clear_springs():
for i in range(n_springs):
spring_length.grad[i] = 0.0
def clear_tensors():
clear_states()
clear_springs()
def main():
x[0, 0] = [0.3, 0.5]
x[0, 1] = [0.3, 0.4]
x[0, 2] = [0.4, 0.4]
spring_anchor_a[0], spring_anchor_b[0], spring_length[0] = 0, 1, 0.1
spring_anchor_a[1], spring_anchor_b[1], spring_length[1] = 1, 2, 0.1
spring_anchor_a[2], spring_anchor_b[2], spring_length[2] = 2, 0, 0.1 * 2**0.5
clear_tensors()
forward('initial')
losses = []
for iter in range(25):
clear_tensors()
with ti.Tape(loss):
forward()
print('Iter=', iter, 'Loss=', loss[None])
losses.append(loss[None])
for i in range(n_springs):
spring_length[i] -= learning_rate * spring_length.grad[i]
for i in range(n_springs):
print(i, spring_length[i])
fig = plt.gcf()
fig.set_size_inches(4, 3)
plt.plot(losses)
plt.title("Spring Rest Length Optimization")
plt.xlabel("Gradient descent iterations")
plt.ylabel("Loss")
plt.tight_layout()
plt.show()
clear_tensors()
forward('final')
if __name__ == '__main__':
main()
import taichi as ti
import os
import math
import numpy as np
import cv2
import matplotlib
import matplotlib.pyplot as plt
real = ti.f32
ti.set_default_fp(real)
num_iterations = 240
n_grid = 128
dx = 1.0 / n_grid
num_iterations_gauss_seidel = 10
p_dims = num_iterations_gauss_seidel + 1
steps = 100
learning_rate = 400
scalar = lambda: ti.var(dt=real)
vector = lambda: ti.Vector(2, dt=real)
v = vector()
div = scalar()
p = scalar()
v_updated = vector()
target = scalar()
smoke = scalar()
loss = scalar()
ti.cfg.arch = ti.cuda
@ti.layout
def place():
ti.root.dense(ti.l, steps * p_dims).dense(ti.ij, n_grid).place(p)
ti.root.dense(ti.l, steps).dense(ti.ij, n_grid).place(v, v_updated, smoke,
div)
ti.root.dense(ti.ij, n_grid).place(target)
ti.root.place(loss)
ti.root.lazy_grad()
# Integer modulo operator for positive values of n
@ti.func
def imod(n, divisor):
ret = 0
if n > 0:
ret = n - divisor * (n // divisor)
else:
ret = divisor + n - divisor * (-n // divisor)
return ret
@ti.func
def dec_index(index):
new_index = index - 1
if new_index < 0:
new_index = n_grid - 1
return new_index
@ti.func
def inc_index(index):
new_index = index + 1
if new_index >= n_grid:
new_index = 0
return new_index
@ti.kernel
def compute_div(t: ti.i32):
for y in range(n_grid):
for x in range(n_grid):
div[t, y, x] = -0.5 * dx * (
v_updated[t, inc_index(y), x][0] - v_updated[t, dec_index(y), x][0] +
v_updated[t, y, inc_index(x)][1] - v_updated[t, y, dec_index(x)][1])
@ti.kernel
def compute_p(t: ti.i32, k: ti.i32):
for y in range(n_grid):
for x in range(n_grid):
a = k + t * num_iterations_gauss_seidel
p[a + 1, y, x] = (
div[t, y, x] + p[a, dec_index(y), x] + p[a, inc_index(y), x] +
p[a, y, dec_index(x)] + p[a, y, inc_index(x)]) / 4.0
@ti.kernel
def update_v(t: ti.i32):
for y in range(n_grid):
for x in range(n_grid):
a = num_iterations_gauss_seidel * t - 1
v[t, y, x][0] = v_updated[t, y, x][0] - 0.5 * (
p[a, inc_index(y), x] - p[a, dec_index(y), x]) / dx
v[t, y, x][1] = v_updated[t, y, x][1] - 0.5 * (
p[a, y, inc_index(x)] - p[a, y, dec_index(x)]) / dx
@ti.kernel
def advect(field: ti.template(), field_out: ti.template(),
t_offset: ti.template(), t: ti.i32):
"""Move field smoke according to x and y velocities (vx and vy)
using an implicit Euler integrator."""
for y in range(n_grid):
for x in range(n_grid):
center_x = y - v[t + t_offset, y, x][0]
center_y = x - v[t + t_offset, y, x][1]
# Compute indices of source cell
left_ix = ti.cast(ti.floor(center_x), ti.i32)
top_ix = ti.cast(ti.floor(center_y), ti.i32)
rw = center_x - left_ix # Relative weight of right-hand cell
bw = center_y - top_ix # Relative weight of bottom cell
# Wrap around edges
# TODO: implement mod (%) operator
left_ix = imod(left_ix, n_grid)
right_ix = left_ix + 1
right_ix = imod(right_ix, n_grid)
top_ix = imod(top_ix, n_grid)
bot_ix = top_ix + 1
bot_ix = imod(bot_ix, n_grid)
# Linearly-weighted sum of the 4 surrounding cells
field_out[t, y, x] = (1 - rw) * (
(1 - bw) * field[t - 1, left_ix, top_ix] +
bw * field[t - 1, left_ix, bot_ix]) + rw * (
(1 - bw) * field[t - 1, right_ix, top_ix] +
bw * field[t - 1, right_ix, bot_ix])
@ti.kernel
def compute_loss():
for i in range(n_grid):
for j in range(n_grid):
ti.atomic_add(
loss,
ti.sqr(target[i, j] - smoke[steps - 1, i, j]) * (1 / n_grid**2))
@ti.kernel
def apply_grad():
# gradient descent
for i in range(n_grid):
for j in range(n_grid):
v[0, i, j] -= learning_rate * v.grad[0, i, j]
def forward(output=None):
for t in range(1, steps):
advect(v, v_updated, -1, t)
compute_div(t)
for k in range(num_iterations_gauss_seidel):
compute_p(t, k)
update_v(t)
advect(smoke, smoke, 0, t)
if output:
smoke_ = np.zeros(shape=(n_grid, n_grid), dtype=np.float32)
for i in range(n_grid):
for j in range(n_grid):
smoke_[i, j] = smoke[t, i, j]
cv2.imshow('smoke', smoke_)
cv2.waitKey(1)
os.makedirs(output, exist_ok=True)
cv2.imwrite("{}/{:04d}.png".format(output, t), 255 * smoke_)
compute_loss()
def main():
target_img = cv2.resize(cv2.imread('taichi.png'),
(n_grid, n_grid))[:, :, 0] / 255.0
for i in range(n_grid):
for j in range(n_grid):
target[i, j] = target_img[i, j]
smoke[0, i, j] = (i // 16 + j // 16) % 2
for opt in range(num_iterations):
with ti.Tape(loss):
output = "outputs/opt{:03d}".format(opt) if opt % 10 == 0 else None
forward(output)
velocity_field = np.ones(shape=(n_grid, n_grid, 3), dtype=np.float32)
for i in range(n_grid):
for j in range(n_grid):
s = 0.2
b = 0.5
velocity_field[i, j, 0] = v[0, i, j][0] * s + b
velocity_field[i, j, 1] = v[0, i, j][1] * s + b
cv2.imshow('velocity', velocity_field)
cv2.waitKey(1)
print('Iter', opt, ' Loss =', loss[None])
apply_grad()
forward("output")
if __name__ == '__main__':
main()
参考文档
1.[link](https://github.com/taichi-dev/taichi)
2.[link](https://github.com/yuanming-hu/taichi_mpm#88-line-version-mit-license-download-c--javascript-versions)
3.[link](https://github.com/yuanming-hu/difftaichi/tree/master/examples)
4.[link](https://mp.weixin.qq.com/s/lS5u7LK1_0Abf9grf8wElw)
5.[link](https://mp.weixin.qq.com/s/H7YAcOTjM1RSEU4HpQRkkA)
6.[link](https://taichi.readthedocs.io/en/latest/meta.html)