圆方树/广义圆方树学习小记（gradually update...）
前言
日前，B组混进了几道仙人掌/无向图上乱搞的问题。正解就是这种我之前听都没听说过的数据结构——圆方树。
定义
仙人掌
先允许我介绍一下仙人掌。
一般而言，仙人掌的定义是：1）无向图；2）每条边最多在一个简单环中。这样就很毒瘤。
但有一些题不大一样，它的定义是这样的（据说国外的定义都是这样）：1）无向图；2）每个点最多在一个简单环中。
不过，你不必太担心，不论它的定义如何，圆方树的构建方法都是别无二致的。
圆方树
圆方树是一种树的结构，用以解决仙人掌相关的问题。
首先，定义原仙人掌上的点为圆点。我们对于每个环，都构建一个方点，令方点向环中的每个节点连边，并删去环上的原有的边。这样，就可以形成一个树的结构。
这里盗一张图：
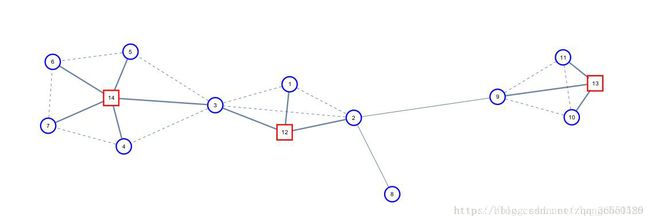
图中的虚边代表原仙人掌中的边；实边代表新建的圆方树中的边。
构造
圆方树的构造方法可以有很多种，因为只要可以缩环就可以。这里介绍两种。
- 类似tarjan求点双的方法。直接贴图。
注意一点，普通圆方树的构造中，一条边连两个点的情况不算作一个点双，也就是说对于这种情况我们不会给它建一个方点。
模板
void tarjan(ll x,ll fa){
ll i,yy,z;
vis[x]=true,dfn[x]=low[x]=++tim,pre[++pre[0]]=x;
fb(i,x){
yy=tov[i];
if (!vis[yy]){
tarjan(yy,i),low[x]=min(low[x],low[yy]);
if (low[yy]>=dfn[x]){
cnt++;
while (pre[pre[0]+1]!=yy){
z=pre[pre[0]--];
link(z,cnt),link(cnt,z);
}
link(x,cnt),link(cnt,x);
}
}else if(i!=(fa^1)) low[x]=min(low[x],dfn[yy]);
}
}
2. 还有一种可能更短比较神奇的方法，连low都不用求。
记ring[i]表示点i是否在一个环里。对于某个点x，我们要从它遍历到它的子节点y时，先将ring[x]赋为0；然后，我们在tarjan的时候，若有某个点x，对于其一条连向点y的出边，满足dfn[y]＜dfn[x]，则表明y为其祖先，我们就找到了一个环，于是建方点、连新边，并使该环中每个节点的ring变为1；于是，回溯回那个点x，若ring依然=0，则表明那个y没有与之形成环，故边(x,y)是树边，在 TG T G 中连上它。
模板
int tim,dfn[N],fat[N];
bool ring[N];
void tarjan(int x)
{
dfn[x]=++tim;
rep(i,final[x])
{
int y=i->v;
if(y!=fat[x])
if(!dfn[y])
{
fat[y]=x; ring[x]=0; tarjan(y);
if(!ring[x]) link(x,y,fin);
}
else
if(dfn[y]int z=x; num++;
for(;z!=y;z=fat[z]) link(num,z,fin), ring[z]=1;
link(num,y,fin); ring[y]=1;
}
}
} 广义圆方树
不要看到“广义”两个字就被吓到了。广义圆方树其实就是把圆方树建到无向图中去。
它的构造方法与普通圆方树略有差异。构造它时，就完完全全地用tarjan跑点双，两点一线的情况也算作一个点双；然后，对于每个点双都建一个方点。
来形象地理解下：
模板
int tim,dfn[N],low[N],fat[N],top,sq;
edge *st[N];
void tarjan(int x)
{
dfn[x]=low[x]=++tim;
repe(i,final[x])
{
int y=i->v;
if(y!=fat[x])
if(!dfn[y])
{
fat[y]=x;
st[++top]=i; tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x])
{
Link(n+(++sq),x);
do
Link(n+sq,st[top]->v);
while(st[top--]!=i);
}
}
else low[x]=min(low[x],dfn[y]);
}
}
性质
圆方树有许多优美的性质。这里列几个出来：
1. 圆方树是一棵无根树，换根不影响形态。
2. 方点间不会相连，一定会有圆点隔开。
3. 圆方树上两点间的路径对应原图中两点的必经路径。
4. ……
对于普通圆方树和广义圆方树，它们还各有一些性质：
普通圆方树
- 圆方树的子树=原仙人掌的子仙人掌。
子仙人掌：以 r 为根的仙人掌上的点 p 的子仙人掌是从仙人掌中除掉 p 到 r 的简单路径上的所有边后， p 所在的连通块。
- 每个方点的父亲均为所在环的根。
- ……
广义圆方树
- 圆点和方点相间分布。圆点间不可能有连边；方点间不可能有连边。
……
总之，具体问题具体分析了。
应用
圆方树有什么用？圆方树大有用处。基本上，仙人掌之类的题，或者是某些无向图上的题，都需要用到圆方树。
比较裸的是计数问题。当然，它还可以与最短路算法、树形DP、虚仙人掌、点分治、树链剖分、动态仙人掌等鬼东西有机结合，形成各种毒瘤题。
例题
然后我也没有做过多少圆方树的题。不过我会慢慢加一些。
【JZOJ3325】【BJOI2013 load】压力（广义圆方树+LCA+树上差分）
【JZOJ3336】【NOI2013模拟】坑带的树（圆方树+计数问题+hashing）