高斯消元法Java、C、Fortran实现代码
Java实现:
package zz;
public class Gauss {
// 高斯消元法
public float[] guass(float[][] arr) {
float[] result = solution(arr);
for (int i = 0; i < arr.length; i++) {
result[i] = arr[i][arr[0].length - 1];
}
System.out.println("高斯消元之后:");
printArr(arr);
for (float f : result) {
System.out.print(f + " ");
}
return result;
}
/*
* 结果在行列式中 所以 列式比行数多1
*/
public float[] solution(float[][] arr) {
int row = arr.length; // 行数
int col = arr[0].length; // 列数
// System.out.println("row = " + row + " col = " + col);
float[] result = new float[row]; // 有多少个方程就有多少个未知数, 所以结果的个数为 行数
for (int i = 0; i < row; i++) {
int maxRow = SelectIndex(arr, i);
// 寻找最大行、交换
if (maxRow != i) {
swapRow(arr, i, maxRow);
}
// 归一化 当前行 每一个元素都除以当前 arr[i][i] 上的元素,归一化
float divNum = arr[i][i];
for (int k = i; k < col; k++) { // 当前行 的每一列元素都除以这个数
arr[i][k] /= divNum;
}
// 用这个1, 消去下面所有行的数
arr = elimination(arr, i);
}
// System.out.println("回代啦");
// 回代 从最后一行开始
backProgram(arr);
return result;
}
/*
* 从最后一行回代,得到结果
*/
public float[][] backProgram(float[][] arr) {
int row = arr.length; // 行
int col = arr[0].length; // 列
for (int i = row - 1; i >= 0; i--) {
for (int j = i - 1; j >= 0; j--) {
// System.out.println("arr[" + j + "][" + (col - 1) + "] = " + arr[j][col - 1]);
// System.out.println("arr[" + j + "][" + i + "] = " + arr[j][i]);
// System.out.println("arr[" + i + "][" + i + "] = " + arr[i][i]);
// System.out.println("arr[" + j + "][" + i + "] * arr[" + i + "][" + (col - 1) + "] = "
// + arr[j][i] * arr[i][col - 1]);
// printArr(arr);
arr[j][col - 1] -= arr[j][i] * arr[i][col - 1];
arr[j][i] = 0;
// printArr(arr);
}
}
return arr;
}
/*
* 用当前行消去下面的所有元素
*/
public float[][] elimination(float[][] arr, int i) {
int row = arr.length;
int col = arr[0].length;
float subNum;
for (int k = i + 1; k < row; k++) { // i行消去下面的行
subNum = arr[k][i];
for (int j = i; j < col; j++) {
arr[k][j] -= (arr[i][j] * subNum);
}
}
return arr;
}
/*
* arr 为行列式 i行,j列 寻找 i -> row 这些行中 j列上最大的元素 并返回该行的下标
*/
public int SelectIndex(float[][] arr, int j) {
int row = arr.length;
int index = j;
// 寻找 j列中最大的元素的下标
for (int k = j; k < row; k++) {
if (Math.abs(arr[k][j]) > Math.abs(arr[index][j])) {
index = k;
}
}
return index;
}
/*
* 交换 i, j 两行上的所有元素
*/
public float[][] swapRow(float[][] arr, int i, int j) {
int col = arr[0].length; // 行列式的列数
float tmp;
for (int k = 0; k < col; k++) {
tmp = arr[i][k];
arr[i][k] = arr[j][k];
arr[j][k] = tmp;
}
return arr;
}
public void printArr(float arr[][]) {
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr[0].length; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
System.out.println();
}
public static void main(String[] args) {
float arr[][] = { { 2, 3, 11, 5, 2 }, { 1, 1, 5, 2, 1 }, { 2, 1, 3, 2, -3 }, { 1, 1, 3, 3, -3 } };
Gauss gauss = new Gauss();
System.out.println("高斯消元求解前:");
gauss.printArr(arr);
gauss.guass(arr);
}
}
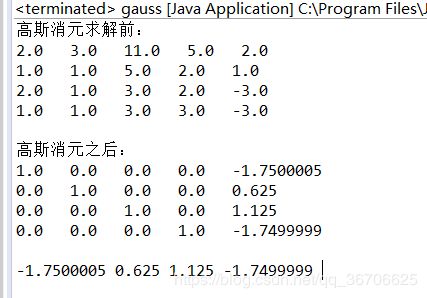
运行结果:
C语言实现:
#include "stdio.h"
#include "math.h"
float *gauss(float *arr, int row, int col);
float *solution(float *arr, int row, int col);
float *backProgram(float *arr, int row, int col);
float *elimination(float *arr, int row, int col, int i);
int SelectIndex(float *arr, int row, int col, int i);
float *swapRow(float *arr, int row, int col, int i, int j);
void printArr(float *arr)
{
for(int i = 0; i < 4; i++)
{
for(int j = 0; j < 5; j++)
{
printf("%f ", arr[i * 5 + j]);
}
printf("\n");
}
}
// 高斯消元函数
float *gauss(float *arr, int row, int col)
{
float *result = solution(arr, row, col);
return result;
}
// row 为行数, col为列数,
float *solution(float *arr, int row, int col)
{
for(int i = 0; i < row; i++)
{
// printf("变化前来一下\n");
// printArr(arr);
int maxRow = SelectIndex(arr, row, col, i);
if(maxRow != i)
{
swapRow(arr, row, col, i, maxRow);
}
float divNum = arr[i * col + i];
for(int k = i; k < col; k++)
{
arr[i * col + k] /= divNum;
}
// printf("变化后来一下\n");
// printArr(arr);
arr = elimination(arr, row, col, i);
}
backProgram(arr, row, col);
return arr;
}
// 回代、求值
float *backProgram(float *arr, int row, int col)
{
for(int i = row - 1; i>= 0; i--)
{
for(int j = i - 1; j >= 0; j--)
{
arr[j * col + col - 1] -= arr[j * col + i] * arr[i * col + col - 1];
arr[j * col + i] = 0;
}
}
return arr;
}
//消去当前行下面的所有元素
float *elimination(float *arr, int row, int col, int i)
{
float subNum;
for(int k = i + 1; k < row; k++) // 当前行到下面的所有行的循环
{
subNum = arr[k * col + i];
for(int kk = i; kk < col; kk++) // 这一行中 列的处理
{
arr[k * col + kk] -= (arr[i * col + kk] * subNum);
}
}
return arr;
}
// 求最大行
int SelectIndex(float *arr, int row, int col, int i)
{
int index = 0;
float max = 0;
for(int k = i * col + i; k < row * col; k += col)
{
if(fabs(max) < fabs(arr[k]))
{
max = arr[k];
index = k;
}
}
return index / col;
}
// 两行交换
float *swapRow(float *arr, int row, int col, int i, int j)
{
float tmp;
for(int k = 0; k < col; k++)
{
tmp = arr[i * col + k];
arr[i * col + k] = arr[j * col + k];
arr[j * col + k] = tmp;
}
return arr;
}
// 主函数
int main()
{
float arr[] = {2, 3, 11, 5, 2,
1, 1, 5, 2, 1,
2, 1, 3, 2, -3,
1, 1, 3, 3, -3};
printf("高斯消元之前:\n");
printArr(arr);
float *a = gauss(arr, 4, 5);
printf("\n高斯消元求解后:\n");
printArr(arr);
return 0;
}
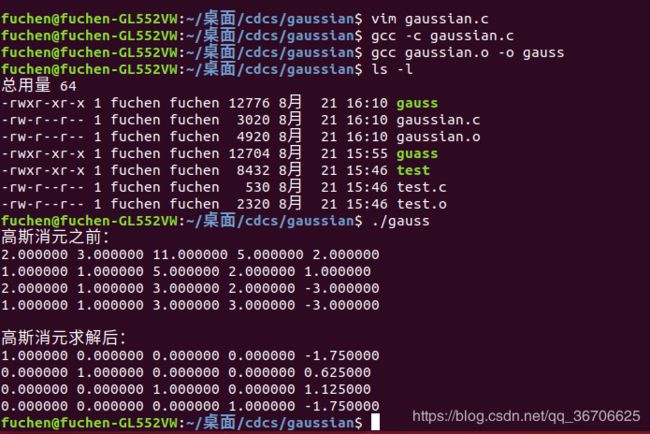
运行结果如图:
Fortran实现:
SUBROUTINE printArr(arr, row, col) ! 数组打印输出函数
IMPLICIT NONE
INTEGER, INTENT(IN) :: row, col ! 行列式的行列
REAL, DIMENSION(row * col), INTENT(INOUT) :: arr
INTEGER :: i, j
forCol: DO i = 1, row
forRow: DO j = 1, col
WRITE(*, 100, advance='no') arr(i * col + j - col)
100 FORMAT (1F10.4)
END DO forRow
WRITE(*,*)
END DO forCol
END SUBROUTINE printArr
! 高斯消元主程序
SUBROUTINE solution(arr, row, col)
IMPLICIT NONE
INTEGER, INTENT(IN) :: row, col
REAL, DIMENSION(row * col), INTENT(INOUT) :: arr
INTEGER :: i, j, maxRow, k
REAL :: divNum
forROW: DO i = 1, row
! 寻找最大元
maxRow = i
! WRITE(*,*) '打印出来,找bug'
! CALL PrintArr(arr, 4, 5)
CALL selectIndex(arr, row, col, maxRow)
IF (maxRow /= i) THEN
CALL swapRow(arr, row, col, i, maxRow)
END IF
! WRITE(*,*) '行交换之后是咋样子的呢'
! CALL PrintArr(arr, 4, 5)
! WRITE(*,*)
divNum = arr(i * col - col + i)
DO k = i, col
arr(i * col - col + k) = arr(i * col - col + k) / divNum
END DO
CALL elimination(arr, row, col, i)
END DO forRow
CALL backProgram(arr, row, col)
END SUBROUTINE solution
! 回代、求解
SUBROUTINE backProgram(arr, row, col)
IMPLICIT NONE
INTEGER, INTENT(IN) :: row, col
REAL, DIMENSION(row * col), INTENT(INOUT) :: arr
INTEGER :: i, j
forRow : DO i = row, 1, -1
forCol : DO j = i - 1, 1, -1
! WRITE(*,*) 'i =', i, ' j =', j
arr(j * col) = arr(j * col) - arr(j * col - col + i) * arr(i * col)
arr(j * col - col + i) = 0
END DO forCol
! WRITE(*,*)
END DO forRow
END SUBROUTINE backProgram
!消去当前行下面的元素
SUBROUTINE elimination(arr, row, col, k)
IMPLICIT NONE
INTEGER, INTENT(IN) :: row, col, k
REAL, DIMENSION(row * col), INTENT(INOUT) :: arr
INTEGER :: i, j
REAL :: subNum ! 临时变量,用于消去其他的数
!WRITE(*,*)'消去元素前'
!CALL PrintArr(arr, 4, 5)
forRow : DO i = k + 1, row
subNum = arr(i * col - col + k)
forCol : DO j = k, col
arr(i * col - col + j) = arr(i * col - col + j) - (arr(k * col - col + j) * subNum)
END DO forCol
END DO forRow
!WRITE(*,*) '消除完毕!'
!CALL PrintArr(arr, 4, 5)
!WRITE(*,*)
END SUBROUTINE elimination
! 寻找最大元的方法
SUBROUTINE selectIndex(arr, row, col, k)
IMPLICIT NONE
INTEGER, INTENT(IN) :: row, col
INTEGER, INTENT(INOUT) :: k
REAL, DIMENSION(row * col), INTENT(INOUT) :: arr
INTEGER :: index, i
REAL :: max = 0
index = k ! 初始化一下, 找不到自己就是最大的
max = 0 ! 不初始化一下, 值一直是上一次的值 zz
!WRITE(*,*)'初始化一下 max =', max
forMax: DO i = k, row
! WRITE(*,*) 'max =', max, 'ABS(arr(i)) =', ABS(arr(i * col - col + k)), 'max < arr ?',&
! (ABS(max) < ABS(arr(i * col - col + k)))
IF (ABS(max) < ABS(arr(i * col - col + k))) THEN
max = arr(i * col - col + k)
! WRITE(*,*)'进来了比他小进来了 i = ', i, 'max =', max, ' arr = ', arr(i * col -col +k)
index = i
! WRITE(*,*) '这个是大于还是小于嘛 max =', max
END IF
END DO forMax
k = index ! 传递回去
END SUBROUTINE selectIndex
! 交换两行的函数
SUBROUTINE swapRow(arr, row, col, i, j)
IMPLICIT NONE
INTEGER, INTENT(IN) :: row, col, i, j
REAL, DIMENSION(row * col), INTENT(INOUT) :: arr
REAL :: tmp ! 临时变量,用于交换两个数
INTEGER :: k
!WRITE(*,*) '真的需要交换吗? i =', i, ' j =', j
DO k = 1, col
! WRITE(*,*) '在行交换里面输出'
! CALL PrintArr(arr, 4, 5)
! WRITE(*,*)
tmp = arr(i * col - col + k)
arr(i * col - col + k) = arr(j * col - col + k)
arr(j * col - col + k) = tmp
END DO
END SUBROUTINE swapRow
PROGRAM gaussian ! 高斯消元主体函数
IMPLICIT NONE
REAL, DIMENSION(20):: arr
arr = [2, 3, 11, 5, 2, &
1, 1, 5, 2, 1, &
2, 1, 3, 2, -3,&
1, 1, 3, 3, -3]
WRITE(*,*) '高斯消元前:'
CALL printArr(arr, 4, 5)
CALL solution(arr, 4, 5)
WRITE(*,*) '高斯消元后:'
CALL printArr(arr, 4, 5)
END PROGRAM gaussian
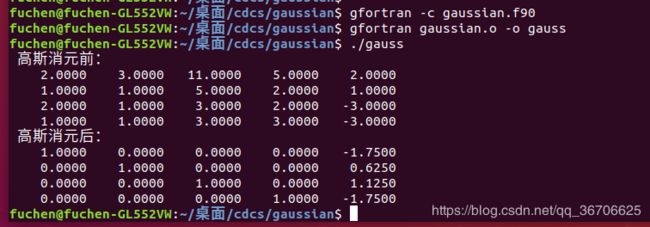
运行结果图: