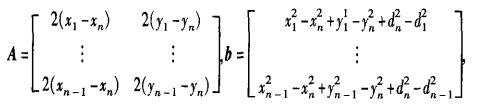【UWB 定位】室内定位 三边定位算法
最近在整UWB室内定位,看到一些简单的测距数据解算算法,记录一下。
测
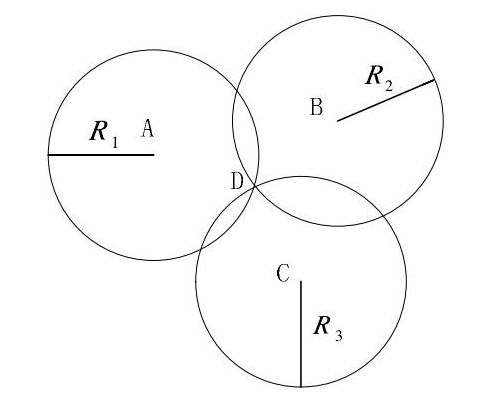
在基于测距的定位算法中,三边测量法是比较简单的算法,算法原理为:平面上有三个不共线的基站 A,B,C,和一个未知终端 D,并已测出三个基站到终端D的距离分别为R1,R2,R3,则以三个基站坐标为圆心,三基站到未知终端距离为半径可以画出三个相交的圆,如图下图所示,未知节点坐标即为三圆相交点。
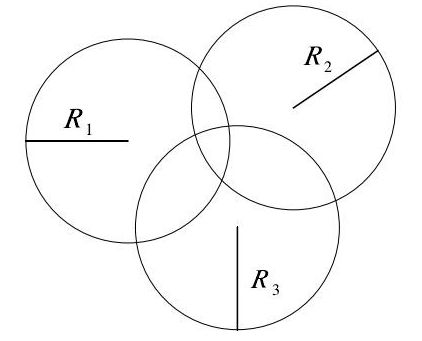
然而,在实际测量中,往往由于测量的误差,使三个圆并不交于一点,而相交于一块区域,如下图所示。在此种情况下,便需用其他算法进行求解,如极大似然估计法,最小二乘法进行估计,或者使用三角形质心算法。
这里,我们的算法采用最小二乘法求近似解,并针对n个基站(n≥3),已知n个基站的坐标分别为 (),(),…,() ,未知终端坐标为() ,由以下步骤求解:
①:建立信标节点与未知节点距离方程组
②:上边方程组为非线性方程组,用方程组中前n-1个方程减去第n个方程后,得到线性化的方程:
![]()
其中:
③:用最小二乘法求解上边方程得:
X 便是未知终端的坐标计算值。
3.2.2 加权三边定位算法
由无线信号强度渐变模型可以发现,当定位终端离基站距离越远时,接收到的RSSI值变化会越来越小,这就会导致距离越远,基站与定位终端的距离误差越大,相应的造成定位误差变大,由此,我们可以采取加权的思想,将距离小的(精确度高)赋予较大的权值,距离大的(精确度低)的赋予较小的权值。
首先将基站分组。对收集到的所有基站,经由id分为组n后,求组合数C(n,3),并对每组分别进行三边定位;接着根据距离越大定位误差越大的原则,赋以权值(为每个基站到定位终端测得的距离)。最后,由每个组合得到的结果加权得到最终的定位结果。
3.2.3 加权三角形质心定位算法
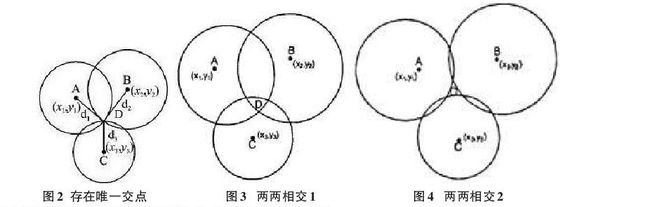
该算法的思想是对收集到的所有基站,经由id分为组n后,求组合数C(n,3),然后对每一个组合的三个基站,以每个基站坐标为圆心,测得的基站到定位终端距离为半径画圆,然后根据交点组成的三角形,求其质心,即为测得的终端坐标。大体如下:
然后,根据距离越大定位误差越大的原则,赋以权值(为每个基站到定位终端测得的距离)。最后,由每个组合得到的结果加权得到最终的定位结果。 然而,由于误差的存在,且测量时位置并不在每个组合所构成的三角形中间位置,因此,当误差大时,往往所构成的圆是没有交点的(三个圆必须两两存在交点,否则不能用该方法)。
带推理公式版算法讲解:
Trilateration(三边测量)是一种常用的定位算法:
- 已知三点位置 (x1, y1), (x2, y2), (x3, y3)
- 已知未知点 (x0, y0) 到三点距离 d1, d2, d3
以 d1, d2, d3 为半径作三个圆,根据毕达哥拉斯定理,得出交点即未知点的位置计算公式:
( x1 - x0 )2 + ( y1 - y0 )2 = d12
( x2 - x0 )2 + ( y2 - y0 )2 = d22
( x3 - x0 )2 + ( y3 - y0 )2 = d32解法推导
![]()
设未知点位置为 (x, y), 令其中的第一个球形 P1 的球心坐标为 (0, 0),P2 处于相同纵坐标,球心坐标为 (d, 0),P3 球心坐标为 (i, j),三个球形半径分别为 r1, r2, r3,z为三球形相交点与水平面高度。则有:
r12 = x2 + y2 + z2
r22 = (x - d)2 + y2 + z2
r32 = (x - i)2 + (y - j)2 + z2当 z = 0 时, 即为三个圆在水平面上相交为一点,首先解出 x:
x = (r12 - r22 + d2) / 2d将公式二变形,将公式一的 z2 代入公式二,再代入公式三得到 y 的计算公式:
y = (r12 - r32 - x2 + (x - i)2 + j2) / 2j来自:https://github.com/megagao/IndoorPos
http://www.justinablog.com/archives/1066