线性回归算法小结

线性回归算法使用小结

利用sklearn实现

最小二乘法

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import pandas as pd

# 加载内置波士顿房价数据集
boston=load_boston()
x=pd.DataFrame(boston.data,columns=boston.feature_names)
y=pd.DataFrame(boston.target)

# 将数据切分成训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3)

# 建立线性回归模型
lr=LinearRegression()
lr.fit(x_train,y_train) # 拟合数据
print('特征系数：',lr.coef_,sep='\n')
print('截距：',lr.intercept_,sep='\n',end='\n\n')
print('获取建模所使用的参数：',lr.get_params())

# 预测数据
y_pred=lr.predict(x_test)

特征系数：
[[-1.24914533e-01  6.09059000e-02 -2.83820784e-02  1.38369307e+00
  -1.78307834e+01  2.81096780e+00 -3.40144761e-03 -1.71018904e+00
   4.29837992e-01 -1.80235782e-02 -1.01324531e+00  8.81491767e-03
  -5.21179038e-01]]
截距：
[46.65946307]

获取建模所使用的参数： {'copy_X': True, 'fit_intercept': True, 'n_jobs': 1, 'normalize': False}

此模型的评价指标是： R Squared

即：R^2 = 1 - [ (y_true-y_pred)^2.sum() - (y_true-y_true.mean())^2.sum() ]
解释：
分子是我们的模型预测产生的错误，分母是基础模型预测生产的错误，因此R2可以理解为，自己的模型拟合住的数据
推论：
1.R2 <= 1
2.R2越大越好，当自己的预测模型不犯任何错误时：R2 = 1
3.当我们的模型等于基准模型时：R2 = 0
4.如果R2 < 0，说明学习到的模型还不如基准模型。 # 注：很可能数据不存在任何线性关系，用线性回归之前可以先对数据进行相关性检验，或者先对数据的残差分布进行判定
3）公式变形

print(lr.score(x_test,y_test))

0.6990237712282111

Ridge回归

Ridge回归是在普通线性回归模型的基础上添加了 L2正则化惩罚项，即：|| y - Xw || ^ 2_2 + alpha * || w || ^ 2_2

目的是减小系数大小(一般认为，系数越大，数据偏移一点都会对结果造成很大影响)，防止过拟合，提高模型的泛化能力。
L2正则化即将系数求平方和再求平方根，可以看做系数向量的欧式距离，惩罚项系数alpha越小，惩罚力度越小

from sklearn.linear_model import Ridge
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
import pandas as pd

# 加载内置波士顿房价数据集
boston=load_boston()
x=pd.DataFrame(boston.data,columns=boston.feature_names)
y=pd.DataFrame(boston.target)

# 将数据切分成训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3)

# 建立Ridge回归模型
rd=Ridge(alpha=0.1) # 设置惩罚项系数
rd.fit(x_train,y_train) # 拟合数据
print('特征系数：',rd.coef_,sep='\n')
print('截距：',rd.intercept_)
print('模型参数：',rd.get_params())

# 预测数据
y_pred=rd.predict(x_test)

特征系数：
[[-1.20775318e-01  4.75727961e-02  2.18627981e-02  1.82571026e+00
  -1.62126817e+01  3.06646987e+00  1.08558784e-02 -1.14498346e+00
   3.31016659e-01 -1.35327244e-02 -9.92745408e-01  8.03019669e-03
  -5.73991996e-01]]
截距： [40.22858606]
模型参数： {'alpha': 0.1, 'copy_X': True, 'fit_intercept': True, 'max_iter': None, 'normalize': False, 'random_state': None, 'solver': 'auto', 'tol': 0.001}

此模型的评价指标是： R Squared

print(rd.score(x_test,y_test))

0.6809481000084785

Ridge回归超参数估计

使用的是留一交叉验证

from  sklearn.linear_model import RidgeCV

alphas=[0.01,0.1,1,10]
rdc=RidgeCV(alphas=alphas).fit(x_train,y_train)
print('特征系数',rdc.coef_,sep='\n')
print('截距',rdc.intercept_)
print('最优参数(惩罚系数)：',rdc.alpha_)
print('模型参数：',rdc.get_params)
print(' R Squared评价:',rdc.score(x_test,y_test))
y_pred=rdc.predict(x_test) # 用最优参数对模型进行预测

特征系数
[[-1.21387385e-01  4.74171306e-02  2.83970619e-02  1.83493901e+00
  -1.75717861e+01  3.06239113e+00  1.20527890e-02 -1.16219133e+00
   3.34070823e-01 -1.34285963e-02 -1.00666168e+00  7.92098925e-03
  -5.72686031e-01]]
截距 [41.12730195]
最优参数(惩罚系数)： 0.01
模型参数： 
 R Squared评价: 0.680996221102513

Lasso回归

Lasso是在普通线性回归的基础上添加了L1正则化惩罚项，即：(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1 ，使用坐标下降法进行优化

目的同样是减小系数大小，防止数据过拟合，提高模型的泛化能力
L1正则化即将系数取绝对值求和，可以产生稀疏矩阵

from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
import pandas as pd

# 加载内置波士顿房价数据集
boston=load_boston()
x=pd.DataFrame(boston.data,columns=boston.feature_names)
y=pd.DataFrame(boston.target)

# 将数据切分成训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3)

# 建立Lasso回归模型
ls=Lasso(alpha=0.1) # 设置学习率
ls.fit(x_train,y_train) # 拟合数据
print('特征系数：',ls.coef_,sep='\n')
print('截距：',ls.intercept_)
print('模型参数：',ls.get_params())

特征系数：
[-0.09911921  0.04747767 -0.04526676  0.96803671 -0.          3.40965512
 -0.00733181 -1.2155376   0.25825724 -0.01263228 -0.89275052  0.0110484
 -0.61670666]
截距： [29.59067791]
模型参数： {'alpha': 0.1, 'copy_X': True, 'fit_intercept': True, 'max_iter': 1000, 'normalize': False, 'positive': False, 'precompute': False, 'random_state': None, 'selection': 'cyclic', 'tol': 0.0001, 'warm_start': False}

此模型的评价指标是： R Squared

print(ls.score(x_test,y_test)) 

0.7409344439332732

Lasso回归的超参数估计

使用的是k折交叉验证

from sklearn.linear_model import LassoCV
import numpy as np

alphas=[0.01,0.1,1,10]
lscv=LassoCV(alphas=alphas)
lscv.fit(x_train,np.array(y_train).ravel())
print('特征系数',lscv.coef_,sep='\n')
print('截距',lscv.intercept_)
print('最优参数(惩罚系数)：',lscv.alpha_)
print('模型参数：',lscv.get_params)
print(' R Squared评价:',lscv.score(x_test,y_test))
y_pred=lscv.predict(x_test) # 使用最优参数进行预测

特征系数
[-1.07397859e-01  4.48454887e-02 -1.13456679e-03  2.86217142e+00
 -1.48199123e+01  3.50434179e+00 -6.19270015e-04 -1.52004725e+00
  2.98320063e-01 -1.17941801e-02 -1.05277149e+00  1.04166291e-02
 -5.69743141e-01]
截距 39.229289518988715
最优参数(惩罚系数)： 0.01
模型参数： 
 R Squared评价: 0.7544059532981564

手动实现

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
import numpy as np
import seaborn as sns

# 线性回归
class LinearRegression(object):
    
    # 正规方程 
    def ne_fit(self,X,y):
        X=np.c_[X,np.ones((X.shape[0],1))] # 将截距项加入特征矩阵
        X_T=X.T # 转置矩阵
        X_inv=np.linalg.inv(X_T.dot(X)) # 构造逆矩阵
        theta=X_inv.dot(X_T).dot(y) # 参数及截距矩阵
        LinearRegression.params= theta[:-1]
        LinearRegression.intercept=theta[-1]
        LinearRegression.theta=theta
        
    # 梯度下降
    def gd_fit(self,X,y,alpha,maxites):
        X=np.c_[X,np.ones((X.shape[0],1))]
        theta=np.ones((X.shape[1],1)) # 初始化参数值
        X_T=X.T
        for i in range(0,maxites):
            loss=X.dot(theta)-y # 损失函数
            gradient=X_T.dot(loss)/X.shape[0] # 梯度
            theta=theta-alpha*gradient # 迭代theta
        LinearRegression.params= theta[:-1]
        LinearRegression.intercept=theta[-1]
        LinearRegression.theta=theta
        
    def predict(self,X):
        X=np.c_[X,np.ones((X.shape[0],1))]
        return X.dot(self.theta)

# 加载内置波士顿房价数据集
boston=load_boston()
X=pd.DataFrame(boston.data,columns=boston.feature_names)
X=pd.DataFrame(X['RM'].head(100))
y=pd.DataFrame(boston.target).head(100)
x_train=X.values
y_train=y.values
print('x_train: ',x_train.shape)
print('y_train:',y_train.shape)

x_train:  (100, 1)
y_train: (100, 1)

x_test=np.arange(x_train.min(),x_train.max().max(),0.01)

# 正规方程
LR_ne=LinearRegression()
LR_ne=LinearRegression()
LR_ne.ne_fit(x_train,y_train)
y_pred_ne=LR_ne.predict(x_test)
print('正规方程：')
print('系数:',LR_ne.params)
print('截距:',LR_ne.intercept.shape,end='\n\n')

# 梯度下降
LR_gd=LinearRegression()
a=0.1
count=100
LR_gd.gd_fit(x_train,y_train,alpha=0.01,maxites=30000)
y_pred_gd=LR_gd.predict(x_test)
print('梯度下降：')
print('系数:',LR_gd.params)
print('截距:',LR_gd.intercept.shape)

正规方程：
系数: [[10.2234634]]
截距: (1,)

梯度下降：
系数: [[9.07742007]]
截距: (1,)

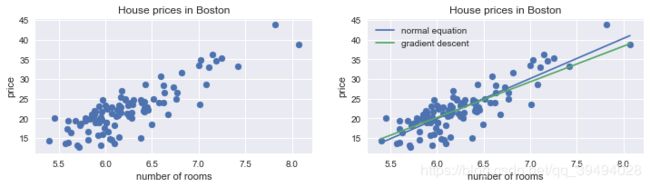
# 每栋住宅的房间数与房价的关系图
sns.set()
fig=plt.figure(figsize=(12,6))
ax1=fig.add_subplot(221)
ax1.scatter(X,y)
plt.title('House prices in Boston')
plt.xlabel('number of rooms')
plt.ylabel('price')

# 用一条直线来拟合数据
ax2=fig.add_subplot(222)
plt.scatter(X,y)                      
plt.plot(x_test,y_pred_ne,label='normal equation')
plt.plot(x_test,y_pred_gd,label='gradient descent')
plt.title('House prices in Boston')
plt.xlabel('number of rooms')
plt.ylabel('price')
plt.legend()

!png