CodeForces 1167 E.Range Deleting & F.Scalar Queries
(有任何问题欢迎留言或私聊 && 欢迎交流讨论哦
Catalog
文章目录
- Catalog
- Problem:传送门
- E.Range Deleting
- F.Scalar Queries
- Problem Description:
Problem:传送门
Portal
原题目描述在最下面。
E.Range Deleting
- 题意:
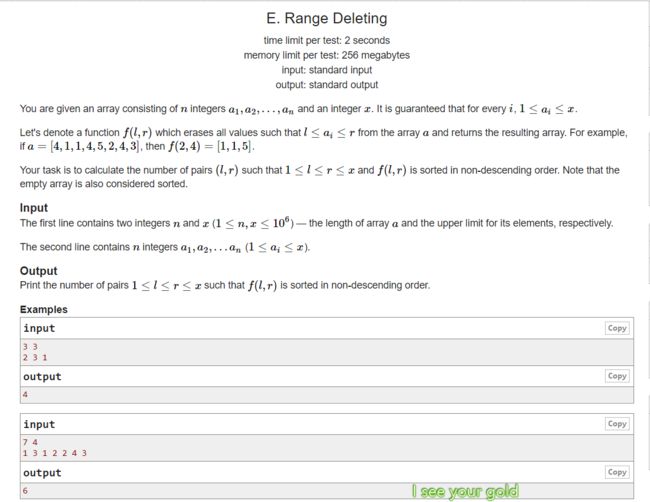
给你一段长度为 n n n值域为 [ 1 , m ] [1, m] [1,m]的序列, n , m ≤ 1 e 6 n,m\le 1e6 n,m≤1e6。
问有多少对 p a i r ( l , r ) pair(l,r) pair(l,r)满足,原序列删除值在 [ l , r ] [l,r] [l,r]范围内的数字后,序列单调不递减。 - 观察:
如果原序列本来就单调不递减,那答案就是 m ∗ ( m + 1 ) / 2 m*(m+1)/2 m∗(m+1)/2。
令 l s [ x ] ls[x] ls[x]表示值 x x x第一次出现的位置, r s [ x ] rs[x] rs[x]表示值 x x x最后一次出现的位置。
若序列本来不是单调不递减,就是存在 a , b a,b a,b满足: 1 ≤ a < b ≤ m , r s [ a ] > l s [ b ] 1\le a\lt b\le m,rs[a]\gt ls[b] 1≤a<b≤m,rs[a]>ls[b]。
我们找到第一次出现矛盾的值 x x x和最后一次出现矛盾的值 y y y。即 r s [ x − 1 ] > l s [ x ] rs[x-1]\gt ls[x] rs[x−1]>ls[x], r s [ y ] > l s [ y + 1 ] rs[y]\gt ls[y+1] rs[y]>ls[y+1]。
观察可知: p a i r ( l , r ) pair(l,r) pair(l,r)必须满足: l ≤ x ∣ ∣ r ≥ y l\le x\;||\;r\ge y l≤x∣∣r≥y。 - 解析:
从上面我们得到了 p a i r ( l , r ) pair(l,r) pair(l,r)种 l l l的上界和 r r r的下界。
考虑枚举 r r r,找到能满足条件的最大的 l l l,那么剩下的 1 , 2 , . . . , l − 1 1,2,...,l-1 1,2,...,l−1做左端点肯定也是满足条件的 p a i r pair pair。这个道理应该很明显。
显然如果你从大到小的枚举 r r r,他们满足条件的最大的 l l l肯定是单调不递增的。
然后就随便 O ( n ) O(n) O(n)计数了。就这样找 l l l,while(rs[x-1] > ls[i+1]) -- x;
因为你只要知道删除 p a i r ( l , r ) pair(l,r) pair(l,r)后,能满足 r s [ l − 1 ] < l s [ r + 1 ] rs[l-1]\lt ls[r+1] rs[l−1]<ls[r+1]即可。 - 细节:
因为有的数字没有出现过,所以找 x , y x,y x,y的时候,先离散化一下在找比较方便。
比如: 3 3 3 1 1 1。没有出现 2 2 2,这时候 x = 3 , y = 1 x=3,y=1 x=3,y=1。因为 r s [ 1 ] > l s [ 3 ] rs[1]\gt ls[3] rs[1]>ls[3]。
还有就是对于没出现过的数字他的 l s [ ] 和 r s [ ] ls[]和rs[] ls[]和rs[]怎么赋值呢?
因为在算答案贡献的时候,只关心小数字的 r s [ ] rs[] rs[]和大数字的 l s [ ] ls[] ls[]。
所以对不存在的数就: r s [ x ] = r s [ x − 1 [ , l s [ x ] = l s [ x + 1 ] rs[x]=rs[x-1[,ls[x]=ls[x+1] rs[x]=rs[x−1[,ls[x]=ls[x+1]。 - 总结:
只要你发现了那个观察,这个题就是一个傻逼题啊。
#includeF.Scalar Queries
- 题意:
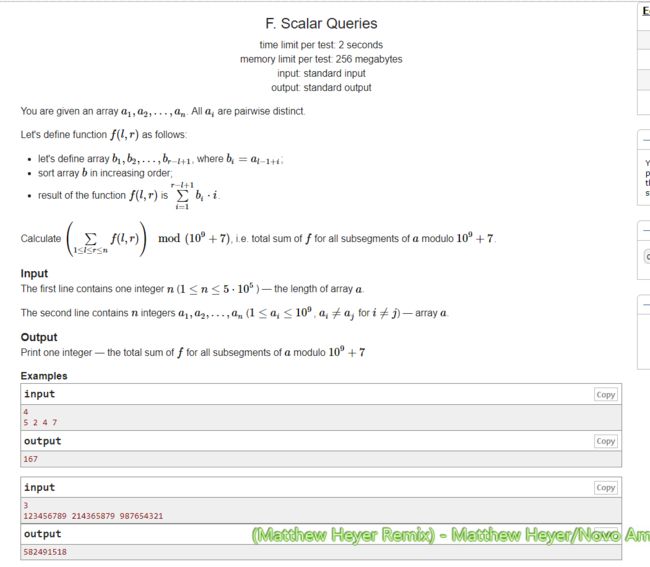
求 ∑ 1 ≤ l ≤ r ≤ n f ( l , r ) \sum_{1\le l\le r\le n}f(l,r) ∑1≤l≤r≤nf(l,r)。 f ( l , r ) = ∑ i = 1 r − l + 1 i ∗ a r [ i ] f(l,r)=\sum_{i=1}^{r-l+1} i*ar[i] f(l,r)=∑i=1r−l+1i∗ar[i],数组 a r ar ar是把原数组的 [ l , r ] [l,r] [l,r]部分从小到大排序后得到的新数组。 - 人尽皆知:
首先 ∑ 1 ≤ l ≤ r ≤ n g ( l , r ) \sum_{1\le l\le r\le n}g(l,r) ∑1≤l≤r≤ng(l,r), g ( l , r ) = ∑ i = l r a [ i ] g(l,r)=\sum_{i=l}^r a[i] g(l,r)=∑i=lra[i]。这个式子应该是随便算的吧?
对每个数字算贡献,数字 x x x包含它的区间有 c n t = i × ( n − i + 1 ) cnt=i\times (n-i+1) cnt=i×(n−i+1)个,贡献就是: x × c n t x\times cnt x×cnt。 - 解析:
还是算单个数字的贡献。
考虑如果有一个数字 y y y,它比 x x x小。那么只要 x , y x,y x,y在一个区间内,这个 y y y的存在肯定会让值 x x x的贡献增加一次。
那么这个 y y y使得 x x x增加的总贡献是多少次呢?
答案是:若 y y y在 x x x前面: p l a c e [ y ] × ( n − p l a c e [ x ] + 1 ) place[y]\times (n-place[x]+1) place[y]×(n−place[x]+1);若 y y y在 x x x后面: p l a c e [ x ] × ( n − p l a c e [ y ] + 1 ) place[x]\times (n-place[y]+1) place[x]×(n−place[y]+1)。
既然这样,我就从前往后和从后往前算两次算贡献即可。
很明显这个东西用一个树状数组维护就可以了。相当于权值线段树吧?就是每个点代表的是权值,维护的是他的下标值,就是他的位置。
看代码就懂了。
#include