第七章：摄像机标定和 3D 重构

第七章：摄像机标定和 3D 重构

本章节你将学习摄像机标定、姿态估计、对极集合和立体图像的深度图等OpenCV摄像机标定和3S重构的相关内容。

更多内容请关注我的GitHub库:TonyStark1997，如果喜欢，star并follow我！

---

一、摄像机标定

---

目标：

本章节你需要学习以下内容:

*我们将了解相机的畸变，相机的内部参数和外部参数等。
*我们将学习如何找到这些参数，和对畸变图像进行修复等。

1、基础

如今市面上便宜的针孔摄像头会给图像带来了很多畸变。两种主要的畸变有两：径向畸变和切向畸变。

由于径向变形，直线会出现弯曲。当我们远离图像中心时，它的效果就会更加明显了。例如，下面显示了一个图像，其中棋盘的两个边缘用红线标记。但是你可以看到图像中边框不是直线而且与红线不重合。所有应该是直线的地方都变成突出的曲线。访问Distortion（光学）了解更多详情。

这种畸变可以通过下面的方程组进行纠正：

$$x_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$

$$y_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)$$

类似地，另一种失真是发生切向失真，因为图像拍摄镜头未完全平行于成像平面对齐。因此，图像中的某些区域可能看起来比预期的更近。它表示如下：

$$x_{distorted}=x+[2p_{1}xy+p_2(r^2+2x^2)]$$

$$y_{distorted}=y+[p_1(r^2+2y^2)+2p_{2}xy]$$

简而言之，我们需要找到五个参数，称为失真系数，由下式给出：

$$Distortioncoefficients=(k_1{k}_2{p}_1{p}_2{k}_3)$$

除此之外，我们还需要找到更多信息，比如摄像机的内部参数和外部参数。内部参数特定于相机。它包括焦距($f_x,f_y$)，光学中心($c_x,c_y$)等信息。它也被称为相机矩阵，仅取决于相机，因此可以只计算一次，然后存储以备将来使用。它表示为3x3矩阵：

$$cameramatrix=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

外部参数对应于旋转向量和平移向量，它可以将3D点的坐标转换到坐标系中。

在 3D 相关应用中，必须要先校正这些畸变。为了找到这些参数，我们必须要提供一些包含明显图案模式的样本图片（比如说棋盘）。我们可以在上面找到一些特殊点（如棋盘的四个角点）。我们起到这些特殊点在图片中的位置以及它们的真是位置。有了这些信息，我们就可以使用数学方法求解畸变系数。这就是整个故事的摘要了。为了得到更好的结果，我们至少需要 10 个这样的图案模式。

2、代码实现

如上所述，我们至少需要 10 图案模式来进行摄像机标定。OpenCV 自带了一些棋盘图像（/sample/cpp/left001.jpg–left14.jpg）, 所以我们可以使用它们。为了便于理解，我们可以认为仅有一张棋盘图像。重要的是在进行摄像机标定时我们要输入一组 3D 真实世界中的点以及与它们对应 2D 图像中的点。2D 图像的点可以在图像中很容易的找到。（这些点在图像中的位置是棋盘上两个黑色方块相互接触的地方）

那么真实世界中的 3D 的点呢？这些图像来源与静态摄像机和棋盘不同的摆放位置和朝向。所以我们需要知道（X，Y，Z）的值。但是为了简单，我们可以说棋盘在 XY 平面是静止的，（所以 Z 总是等于 0）摄像机在围着棋盘移动。这种假设让我们只需要知道 X，Y 的值就可以了。现在为了求 X，Y 的值，我们只需要传入这些点（0,0），（1,0），（2,0）…，它们代表了点的位置。在这个例子中，我们的结果的单位就是棋盘（单个）方块的大小。但是如果我们知道单个方块的大小（加入说 30mm），我们输入的值就可以是（0,0），（30,0），（60,0）…，结果的单位就是 mm。（在本例中我们不知道方块的大小，因为不是我们拍的，所以只能用前一种方法了）。

3D 点被称为 对象点，2D 图像点被称为 图像点。

（1）设置

为了找到棋盘的图案，我们要使用函数 cv2.findChessboardCorners()。我们还需要传入图案的类型，比如说 8x8 的格子或 5x5 的格子等。在本例中我们使用的恨死 7x8 的格子。（通常情况下棋盘都是 8x8 或者 7x7）。它会返回角点，如果得到图像的话返回值类型（Retval）就会是 True。这些角点会按顺序排列（从左到右，从上到下）。

其他：这个函数可能不会找出所有图像中应有的图案。所以一个好的方法是编写代码，启动摄像机并在每一帧中检查是否有应有的图案。在我们获得图案之后我们要找到角点并把它们保存成一个列表。在读取下一帧图像之前要设置一定的间隔，这样我们就有足够的时间调整棋盘的方向。继续这个过程直到我们得到足够多好的图案。就算是我们举得这个例子，在所有的 14 幅图像中也不知道有几幅是好的。所以我们要读取每一张图像从其中找到好的能用的。

其他：除了使用棋盘之外，我们还可以使用环形格子，但是要使用函数cv2.findCirclesGrid() 来找图案。据说使用环形格子只需要很少的图像就可以了。

在找到这些角点之后我们可以使用函数 cv2.cornerSubPix() 增加准确度。我们使用函数 cv2.drawChessboardCorners() 绘制图案。所有的这些步骤都被包含在下面的代码中了：

import numpy as np
import cv2 as cv
import glob

# termination criteria
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)

# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

# Arrays to store object points and image points from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.

images = glob.glob('*.jpg')

for fname in images:
    img = cv.imread(fname)
    gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
    
    # Find the chess board corners
    ret, corners = cv.findChessboardCorners(gray, (7,6), None)
    
    # If found, add object points, image points (after refining them)
    if ret == True:
        objpoints.append(objp)
        
        corners2 = cv.cornerSubPix(gray,corners, (11,11), (-1,-1), criteria)
        imgpoints.append(corners)
        
        # Draw and display the corners
        cv.drawChessboardCorners(img, (7,6), corners2, ret)
        cv.imshow('img', img)
        cv.waitKey(500)
        
cv.destroyAllWindows()

其上绘制有图案的一幅图像如下所示：

（2）标定

在得到了这些对象点和图像点之后，我们已经准备好来做摄像机标定了。

我们要使用的函数是 cv2.calibrateCamera()。它会返回摄像机矩阵，畸变系数，旋转和变换向量等。

ret, mtx, dist, rvecs, tvecs = cv.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)

（3）畸变矫正

现在我们找到我们想要的东西了，我们可以找到一幅图像来对他进行校正了。OpenCV 提供了两种方法，我们都学习一下。不过在那之前我们可以使用从函数 cv2.getOptimalNewCameraMatrix() 得到的自由缩放系数对摄像机矩阵进行优化。如果缩放系数 alpha = 0，返回的非畸变图像会带有最少量的不想要的像素。它甚至有可能在图像角点去除一些像素。如果 alpha = 1，所有的像素都会被返回，还有一些黑图像。它还会返回一个 ROI 图像，我们可以用来对结果进行裁剪。

我们读取一个新的图像（left2.ipg）

img = cv.imread('left12.jpg')
h,  w = img.shape[:2]
newcameramtx, roi = cv.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h))

使用 cv2.undistort() 这是最简单的方法。只需使用这个函数和上边得到的 ROI 对结果进行裁剪。

# undistort
dst = cv.undistort(img, mtx, dist, None, newcameramtx)

# crop the image
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
cv.imwrite('calibresult.png', dst)

使用 remapping 这应该属于“曲线救国”了。首先我们要找到从畸变图像到非畸变图像的映射方程。再使用重映射方程。

# undistort
mapx, mapy = cv.initUndistortRectifyMap(mtx, dist, None, newcameramtx, (w,h), 5)
dst = cv.remap(img, mapx, mapy, cv.INTER_LINEAR)

# crop the image
x, y, w, h = roi
dst = dst[y:y+h, x:x+w]
cv.imwrite('calibresult.png', dst)

两种方法都给出了相同的结果。 请看下面的结果：

mean_error = 0
for i in xrange(len(objpoints)):
    imgpoints2, _ = cv.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv.norm(imgpoints[i], imgpoints2, cv.NORM_L2)/len(imgpoints2)
    mean_error += error
    
print( "total error: {}".format(mean_error/len(objpoints)) )

你会发现结果图像中所有的边界都变直了。

现在我们可以使用 Numpy 提供写函数（np.savez，np.savetxt 等）将摄像机矩阵和畸变系数保存以便以后使用。

3、反向投影误差

我们可以利用反向投影误差对我们找到的参数的准确性进行估计。得到的结果越接近 0 越好。有了内部参数，畸变参数和旋转变换矩阵，我们就可以使用 cv2.projectPoints() 将对象点转换到图像点。然后就可以计算变换得到图像与角点检测算法的绝对差了。然后我们计算所有标定图像的误差平均值。

mean_error = 0
for i in xrange(len(objpoints)):
    imgpoints2, _ = cv.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)
    error = cv.norm(imgpoints[i], imgpoints2, cv.NORM_L2)/len(imgpoints2)
    mean_error += error
    
print( "total error: {}".format(mean_error/len(objpoints)) )

二、姿态估计

---

目标：

本章节你需要学习以下内容:

*我们将学习利用calib3d模块在图像中创建一些3D效果。

1、基础

在上一节的摄像机标定中，我们已经得到了摄像机矩阵，畸变系数等。有了这些信息我们就可以估计图像中图案的姿态，或物体在空间中的位置，比如目标对象是如何摆放，如何旋转等。对一个平面对象来说，我们可以假设 Z=0，这样问题就转化成摄像机在空间中是如何摆放（然后拍摄）的。所以，如果我们知道对象在空间中的姿态，我们就可以在图像中绘制一些 2D 的线条来产生 3D 的效果。我们来看一下怎么做吧。

我们的问题是，在棋盘的第一个角点绘制 3D 坐标轴（X，Y，Z 轴）。X轴为蓝色，Y 轴为绿色，Z 轴为红色。在视觉效果上来看，Z 轴应该是垂直与棋盘平面的。

首先，让我们从先前的校准结果中加载相机矩阵和畸变系数。

import numpy as np
import cv2 as cv
import glob
# Load previously saved data
with np.load('B.npz') as X:
    mtx, dist, _, _ = [X[i] for i in ('mtx','dist','rvecs','tvecs')]

现在让我们创建一个函数，绘制它获取棋盘中的角（使用cv.findChessboardCorners()获得）和轴点来绘制3D轴。

def draw(img, corners, imgpts):
    corner = tuple(corners[0].ravel())
    img = cv.line(img, corner, tuple(imgpts[0].ravel()), (255,0,0), 5)
    img = cv.line(img, corner, tuple(imgpts[1].ravel()), (0,255,0), 5)
    img = cv.line(img, corner, tuple(imgpts[2].ravel()), (0,0,255), 5)
    return img

然后与前面的情况一样，我们创建终止标准，对象点（棋盘中的角点的3D点）和轴点。轴点是3D空间中用于绘制轴的点。我们绘制长度为3的轴（单位将以国际象棋方形尺寸表示，因为我们根据该尺寸校准）。所以我们的X轴是从（0,0,0）到（3,0,0）绘制的，同样。Y轴也一样。对于Z轴，它从（0,0,0）绘制到（0,0，-3）。负值表示它是朝着（垂直于）摄像机方向

criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 30, 0.001)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)

axis = np.float32([[3,0,0], [0,3,0], [0,0,-3]]).reshape(-1,3)

很通常一样我们需要加载图像。搜寻 7x6 的格子，如果发现，我们就把它优化到亚像素级。然后使用函数:cv2.solvePnPRansac() 来计算旋转和变换。但我们有了变换矩阵之后，我们就可以利用它们将这些坐标轴点映射到图像平面中去。简单来说，我们在图像平面上找到了与 3D 空间中的点（3,0,0）,(0,3,0),(0,0,3) 相对应的点。然后我们就可以使用我们的函数 draw() 从图像上的第一个角点开始绘制连接这些点的直线了。搞定！！！

for fname in glob.glob('left*.jpg'):
    img = cv.imread(fname)
    gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
    ret, corners = cv.findChessboardCorners(gray, (7,6),None)
    
    if ret == True:
        corners2 = cv.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)
        
        # Find the rotation and translation vectors.
        ret,rvecs, tvecs = cv.solvePnP(objp, corners2, mtx, dist)
        
        # project 3D points to image plane
        imgpts, jac = cv.projectPoints(axis, rvecs, tvecs, mtx, dist)
        img = draw(img,corners2,imgpts)
        cv.imshow('img',img)
        k = cv.waitKey(0) & 0xFF
        if k == ord('s'):
            cv.imwrite(fname[:6]+'.png', img)
            
cv.destroyAllWindows()

看下面的一些结果。请注意，每个轴的长度为3个方格：

三、渲染立方体

如果要绘制立方体，请按如下方式修改draw()函数和轴点。

修改了draw()函数：

def draw(img, corners, imgpts):
    imgpts = np.int32(imgpts).reshape(-1,2)
    
    # draw ground floor in green
    img = cv.drawContours(img, [imgpts[:4]],-1,(0,255,0),-3)
    
    # draw pillars in blue color
    for i,j in zip(range(4),range(4,8)):
        img = cv.line(img, tuple(imgpts[i]), tuple(imgpts[j]),(255),3)
        
    # draw top layer in red color
    img = cv.drawContours(img, [imgpts[4:]],-1,(0,0,255),3)
    
    return img

修改了轴点。它们是3D空间中立方体的8个角：

axis = np.float32([[0,0,0], [0,3,0], [3,3,0], [3,0,0],
                   [0,0,-3],[0,3,-3],[3,3,-3],[3,0,-3] ])

结果如下图所示：

如果你对计算机图形学和增强现实等感兴趣，可以使用OpenGL渲染更复杂的图形。

三、对极几何

---

目标：

本章节你需要学习以下内容:

*我们将了解多视角几何的基础知识
*我们将看到什么是极点，极线，对极约束等。

1、基础

当我们使用针孔相机拍摄图像时，我们会丢失一些重要的信息，比如图像的深度。或者是图像中的每个点距离相机有多远，因为它是3D到2D的转换。因此一个重要的问题就产生了，使用这样的摄像机我们能否计算除深度信息呢？答案是我们需要使用多个摄像头。我们的眼睛以类似的方式工作，我们使用两个相机（两只眼睛）来判断物体的距离，称为立体视觉。那么让我们看看OpenCV在这个领域提供了什么。

（《学习 OpenCV》一书有大量相关知识）

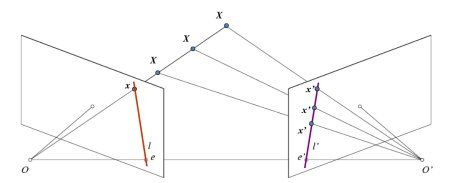
在进入深度图像之前，让我们先了解多视图几何中的一些基本概念。在本节中，我们将讨论极线几何。请参见下图，其中显示了使用两个相机拍摄同一场景图像的基本设置。

如果我们仅使用左侧相机，则无法找到与图像中的点x对应的3D点，因为线OX上的每个点都投影到图像平面上的相同点。但是如果我们也考虑上右侧图像的话，直线 OX 上的点将投影到右侧图像上的不同位置（x’）。所以根据这两幅图像，我们就可以使用三角测量计算出 3D 空间中的点到摄像机的距离（深度）。这就是整个思路。

OX上不同点的投影在右平面（线l’）上形成一条线。我们称它为对应于点x的极线。也就是说，要在右侧图像上找到点x，需要沿着此极线搜索。它应该在这个一维直线的某个地方（想象一下，要找到其他图像中的匹配点，你不需要搜索整个图像，只需沿着极线搜索。因此它提供了更好的性能和准确性）。这称为极线约束。类似地，所有点将在另一图像中具有其对应的极线。平面XOO’称为极线平面。

O和O’是摄像机中心。从上面给出的设置中，可以看到右侧摄像机O’的投影在该点的左侧图像上看到，例如。它被称为极点。极点是通过摄像机中心和图像平面的线的交叉点。类似地，e’是左相机的极点。在某些情况下，你将无法在图像中找到极点，它们可能位于图像之外（这意味着，一台摄像机看不到另一台摄像机）。

所有的极线都通过它的极点。所以为了找到极点的位置，我们可以先找到多条极线，这些极线的交点就是极点。

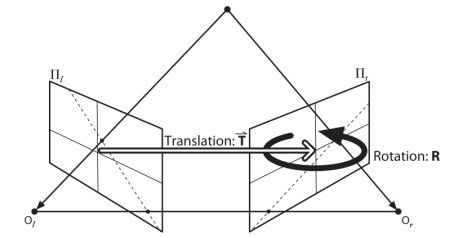
所以在本小节中，我们的重点就是寻找极线和极点。但要找到它们，我们需要另外两个元素，本征矩阵（F）和基本矩阵（E）。本征矩阵包含了物理空间中两个摄像机相关的旋转和平移信息。如下图所示（本图来源自：学习 OpenCV）：

但我们更喜欢用像素坐标进行测量，对吧？基础矩阵 F 除了包含 E 的信息外还包含了两个摄像机的内参数。由于 F包含了这些内参数，因此它可以它在像素坐标系将两台摄像机关联起来。（如果使用是校正之后的图像并通过除以焦距进行了归一化，F=E）。简单来说，基础矩阵 F 将一副图像中的点映射到另一幅图像中的线（极线）上。这是通过匹配两幅图像上的点来实现的。要计算基础矩阵至少需要 8 个点（使用 8 点算法）。点越多越好，可以使用 RANSAC 算法得到更加稳定的结果。

2、代码实现

首先，我们需要在两个图像之间找到尽可能多的匹配，以找到基本矩阵。为此，我们使用SIFT描述符和基于FLANN的匹配器和比率测试。

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

img1 = cv.imread('myleft.jpg',0)  #queryimage # left image
img2 = cv.imread('myright.jpg',0) #trainimage # right image

sift = cv.SIFT()

# find the keypoints and descriptors with SIFT
kp1, des1 = sift.detectAndCompute(img1,None)
kp2, des2 = sift.detectAndCompute(img2,None)

# FLANN parameters
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)

flann = cv.FlannBasedMatcher(index_params,search_params)
matches = flann.knnMatch(des1,des2,k=2)

good = []
pts1 = []
pts2 = []

# ratio test as per Lowe's paper
for i,(m,n) in enumerate(matches):
    if m.distance < 0.8*n.distance:
        good.append(m)
        pts2.append(kp2[m.trainIdx].pt)
        pts1.append(kp1[m.queryIdx].pt)

现在我们有两张图片的最佳匹配列表。让我们找到基本矩阵。

pts1 = np.int32(pts1)
pts2 = np.int32(pts2)
F, mask = cv.findFundamentalMat(pts1,pts2,cv.FM_LMEDS)

# We select only inlier points
pts1 = pts1[mask.ravel()==1]
pts2 = pts2[mask.ravel()==1]

下一步我们要找到极线。我们会得到一个包含很多线的数组。所以我们要定义一个新的函数将这些线绘制到图像中。

def drawlines(img1,img2,lines,pts1,pts2):
    ''' img1 - image on which we draw the epilines for the points in img2
        lines - corresponding epilines '''
    r,c = img1.shape
    img1 = cv.cvtColor(img1,cv.COLOR_GRAY2BGR)
    img2 = cv.cvtColor(img2,cv.COLOR_GRAY2BGR)
    for r,pt1,pt2 in zip(lines,pts1,pts2):
        color = tuple(np.random.randint(0,255,3).tolist())
        x0,y0 = map(int, [0, -r[2]/r[1] ])
        x1,y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ])
        img1 = cv.line(img1, (x0,y0), (x1,y1), color,1)
        img1 = cv.circle(img1,tuple(pt1),5,color,-1)
        img2 = cv.circle(img2,tuple(pt2),5,color,-1)
    return img1,img2

现在我们在两个图像中找到了极线并绘制它们。

# Find epilines corresponding to points in right image (second image) and
# drawing its lines on left image
lines1 = cv.computeCorrespondEpilines(pts2.reshape(-1,1,2), 2,F)
lines1 = lines1.reshape(-1,3)
img5,img6 = drawlines(img1,img2,lines1,pts1,pts2)

# Find epilines corresponding to points in left image (first image) and
# drawing its lines on right image
lines2 = cv.computeCorrespondEpilines(pts1.reshape(-1,1,2), 1,F)
lines2 = lines2.reshape(-1,3)
img3,img4 = drawlines(img2,img1,lines2,pts2,pts1)

plt.subplot(121),plt.imshow(img5)
plt.subplot(122),plt.imshow(img3)
plt.show()

结果如下图所示；

你可以在左侧图像中看到所有的极线都会聚合在右侧图像外部的一个点上，这个点就是极点。

为了得到更好的结果，我们应该使用分辨率比较高和很多非平面点的图像。

四、立体图像的深度图

---

目标：

本章节你需要学习以下内容:

*我们将学习如何从立体图像创建深度图。

1、基础

在上一节中我们学习了对极约束的基本概念和相关术语。如果同一场景有两幅图像的话我们在直觉上就可以获得图像的深度信息。下面是的这幅图和其中的数学公式证明我们的直觉是对的。（图像来源 image courtesy）

上图包含等效三角形。编写等效方程将产生以下结果：

$$disparity=x-x^{\prime }=\frac{Bf}{Z}$$

x 和 x’ 分别是图像中的点到 3D 空间中的点和到摄像机中心的距离。B 是这两个摄像机之间的距离，f 是摄像机的焦距。上边的等式告诉我们点的深度与x 和 x’ 的差成反比。所以根据这个等式我们就可以得到图像中所有点的深度图。

这样就可以找到两幅图像中的匹配点了。前面我们已经知道了对极约束可以使这个操作更快更准。一旦找到了匹配，就可以计算出 disparity 了。让我们看看在 OpenCV 中怎样做吧。

2、代码实现

下面的代码片段显示了创建视差图的简单过程。

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt

imgL = cv.imread('tsukuba_l.png',0)
imgR = cv.imread('tsukuba_r.png',0)

stereo = cv.StereoBM_create(numDisparities=16, blockSize=15)
disparity = stereo.compute(imgL,imgR)
plt.imshow(disparity,'gray')
plt.show()

下图包含原始图像（左）及其视差图（右）。如图所见，结果受到高度噪音的污染。通过调整numDisparities和blockSize的值，你可以获得更好的结果。