卷积神经网络详解(卷积,padding,strided,三维卷积,池化层等知识)
目录
一.边缘检测
1.1 卷积是如何运算的?
1.2 为什么卷积可以做垂直边缘检测呢?卷积是如何工作的?
1.3 如何区分垂直边缘是由深入浅,还是由浅入深的边缘?
二.padding
2.1 卷积中存在的缺点
2.2 问题解决
2.3 两个参数的含义
三.步长strided
3.1 输入和输出的维度
3.2 cross-correlation VS. correlation (深度学习中的卷 vs. 数学中的卷积)
四.立体卷积
4.1 立体卷积的计算
4.2 多个边缘检测器
五.单层卷积网络
5.1 如何构建卷积神经网络的卷积层?(卷积神经网络在某一次的工作原理)
5.2 如何让卷积层从一层传播到下一层?
5.3 卷积的标识
六、池化层
6.1 最大池化
6.2 平均池化(不太常用)
6.3 超级参数
七、卷积神经网络示例
7.1 示例的构建过程详述
7.2 示例中激活值的形状,大小,参数数量
八. 为什么使用卷积?
8.1 参数共享
8.2 稀疏连接
一.边缘检测
1.1 卷积是如何运算的?
对应位相乘,具体方法见另一博文https://blog.csdn.net/qq_40243295/article/details/104391755
卷积运算:
python中是conv_forward
TensorFlow中是td.nn.conv2d
kears中是Conv2D
1.2 为什么卷积可以做垂直边缘检测呢?卷积是如何工作的?
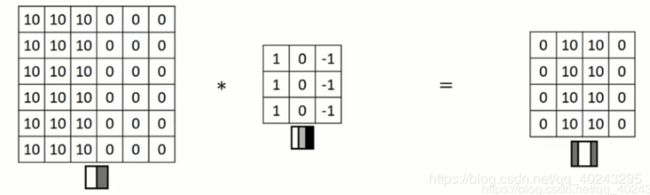
如下图所示:
左侧图:代表输入的6x6的灰度图,10表示白色,0表示灰色
中间图:代表卷积核1、0、-1分别表示白、灰、黑(或者可用浅色,中间不考虑,深色像素来表达)
右侧图:右侧图是通过卷积得到的结果,0、10分别代表灰、白;中间的白色就是检测出来的边缘。但是此时由于输入的图片大小是6x6的所以就会显得检测出来的边缘很宽,如果输入的图片是1000x1000的边缘就会很窄。
1.3 如何区分垂直边缘是由深入浅,还是由浅入深的边缘?
如果将卷积核的9个元素为以下取值,就分别是sobel核与scharr核:
如果将9个元素当做参数,然后进行反向传播算法,将输入图与卷积核进行得到理想的边缘检测,其目标就是理解这9个参数。相比较于这些单纯水平垂直的卷积核,这样的卷积核可以算出45°,75°,81°甚至是任意角度的边缘。所以通过将9个元素当做参数,通过数据反馈,让神经网络自动的去学习它所需的任何卷积核,并且在整幅图上运用此卷积核,依次检测任何的边缘。
要讨论反向传播我们还需要学习一下内容padding和各种卷积的发展,其是卷积神经网络中卷积模块重要的组成部分
二.padding
2.1 卷积中存在的缺点
已知输入像素(nxn),卷积核大小(f x f),可以得到卷积后的图像像素大小(n-f+1 x n-f+1),如图:
由于卷积过程中的两个缺点的存在:
1.原图每经过依次卷积之后,像素就会缩小,因此卷积很多次之后图像就会变得非常小。
2.角落或边缘的像素点信息容易丢失。例如下图:左上角的像素点只被包括了一次,但是中间的像素点被包括了很多次,那么左上角的像素点的数据卷积后就很容易丢失。
2.2 问题解决
因此,我们需要在给原图卷积之前填充一层像素(用0填充),使卷积之后的图片与原图像素相同。
例如原图为6x6,卷积核是3x3,则可以将原图扩充为8x8的(扩充后大小=n-f+1,其中n为原图大小,f为卷积核大小),因此输出还是6x6的图(8-3+1=6)
另外一种表示:将边缘用p表示(扩充了一层此时p=1)。但是计算时,扩充一层就是上下共两行(就是2p),所以表达式是n+2p-f-1 x n+2p-f-1,这就是卷积之后输出的大小,解决了卷积之后图像缩小的问题。
由n=n+2p-1解出p,
p=(f-1)/2
f是卷积层的大小(通常为奇数),n是原图的大小。
6x6的原图中左上角的像素点,扩充后进行卷积,也可以影响好几个框,所以保留了像素点的值,解决了边缘信息易丢失的问题。
2.3 两个参数的含义
三.步长strided
卷积中的步长是构建卷积神经网络的基本操作。
3.1 输入和输出的维度
其是由以下公式决定:
参数:
原图式:n x n
卷积核: f x f
padding: p
stride :s 此处s=2
输出图像像素表达式:[(n+2p-f)/s +1] x [(n+2p-f)/s +1]
如果计算出不是整数,则向下取整
3.2 cross-correlation VS. correlation (深度学习中的卷 vs. 数学中的卷积)
在数学中卷积运算要对原卷积核进行翻转再与原图进行计算。
但从技术上来讲,我们不进行翻转。因此两者是有区分的
省略旋转的原因是:旋转之后就会有(A*B)*C=A*(B*C)的性质,但对深度神经网络不重要,因此我们省略这个双重镜像操作以简化代码,并且神经网络也能正常工作。
四.立体卷积
4.1 立体卷积的计算
灰度图的是6*6*1是一维的
但是彩色图是6*6*3有三个通道数,因此是三维的。卷积核的通道数要与原图的通道数相同,因此卷积核也是三维的。
但是卷积之后的图片是二维的。
通道数channels,也叫三维立体图的深度
左侧27个数与卷积核对于位置数相乘求和,得到卷积后的一个值,移动卷积核对于位的27个值对于相乘求和,以此类推.....
红色边缘检测:R设置为正常,G、B设置为全0
任意颜色检测:R、G、B都设置为正常,具体如图:
4.2 多个边缘检测器
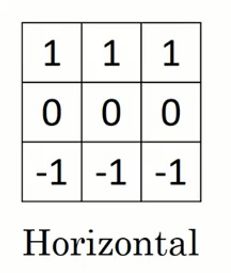
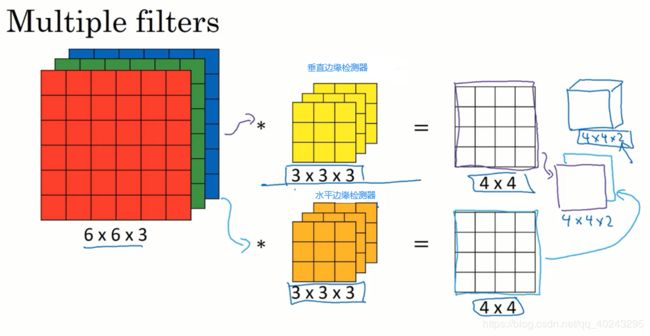
三维下,我们不仅仅想要垂直的边缘检测器,还想要同时检测水平,垂直的,或者45°,70°以及各个方向的边缘检测器,该如何实现?
我们可以使用多个卷积核与原图卷积,然后将卷积后的图依次叠加起来,第一个在叠加图的最上面.....,如图所示:
五.单层卷积网络
5.1 如何构建卷积神经网络的卷积层?(卷积神经网络在某一次的工作原理)
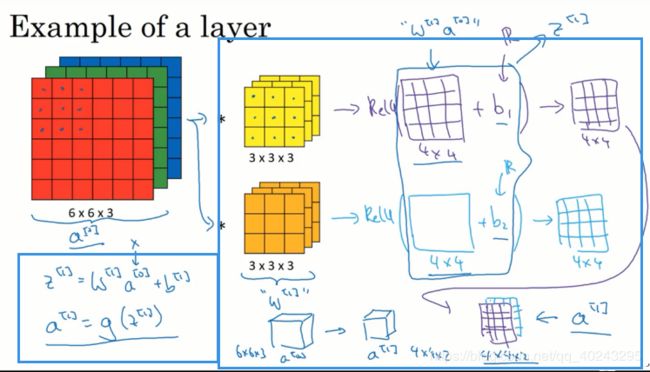
原图分别与各个卷积核卷积,最终各自形成一个卷积神经网络层,然后增加偏差(给卷积神经网络层的16个元素,每个都加同一个偏差),然后应用一个非线性激活函数ReLU,最终得到另一个4x4的矩阵。然后重复我们之前的操作,将这两个矩阵堆叠起来,就变成了一个4x4x2的的矩阵。
5.2 如何让卷积层从一层传播到下一层?
参数:
最初的输入层为a[0],下一层为a[1],第一层的过滤器表示为w[1]
1. 使用线性函数:a[0]w[1],卷积后的结果就是a[0]w[1],即原图与卷积核对应位相乘的结果。
2. 再加上偏差b:变为w[1]a[0]+b,记为z[1],z[1]就是应用激活函数之前的值。
3. 使用激活函数ReLU:g(z[1])就是应用激活函数之后的值,记为a[1],成为神经网络的下一层。
z[1]=w[1]a[0]
然后执行非线性激活函数得到a[1]=g(z[1])
假设有10个过滤器(可以提取10个特征),每个是3x3x3,那么这一层有多少个参数呢?
1个过滤器:3x3x3=27+一个偏差b=28个参数
28x10个=280个参数
注意:无论输入的图片是多大的,参数始终是280个
5.3 卷积的标识
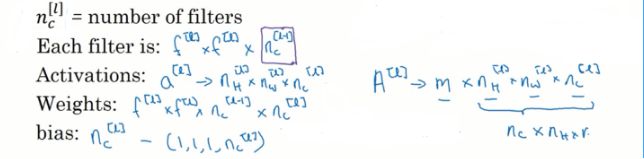
f[l]:l层中过滤器的大小filter size
p[l]:l层的padding
s[l]:l层的步长stride
l层的输入值:即上层的输出层,nh[l-1] x nw[l-1] x nc[l-1](三个分别代表高、宽、通道数)
l层的输出层:nh[l] x nw[l] x nc[l]
输出图片的大小:nh[l] = [(nh[l-1]+2p[l]-f[l])/s[l]]+1向下取整
nw[l] = [(nw[l-1]+2p[l]-f[l])/s[l]]+1向下取整
nc[l]=该层过滤器的数量,过滤器的通道数必须与输入的通道数保持一致
过滤器大小:f[l] x f[l] x nc[l-1]
应用偏差和非线性函数之后,l层的输出的激活值就是a[l],a[l]是一个三维体,即nh[l] x nw[l] x nc[l]
如果执行批量梯度下降,如果有m个例子,就是有m个激活值,A[l]=m x nh[l] x nw[l] x nc[l]
权重参数Weights:f[l] x f[l] x nc[l-1] x nc[l]
偏差bias:每个过滤器都有一个偏差参数,1x1x1xnc[l]
简单卷积网络示意:
典型的卷积网络通常有三层:
-Convolution (Conv)卷积层
-Pooling(pool)池化层
-Fully connected(FC)全连接层
虽然仅适用卷积层也有可能构建出很好的神经网络,但大部分神经网络架构师依然会添加池化层和全连接层。
六、池化层
卷积网络除了卷积层也经常使用池化层,来缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性。
池化类型:最大池化,平均池化
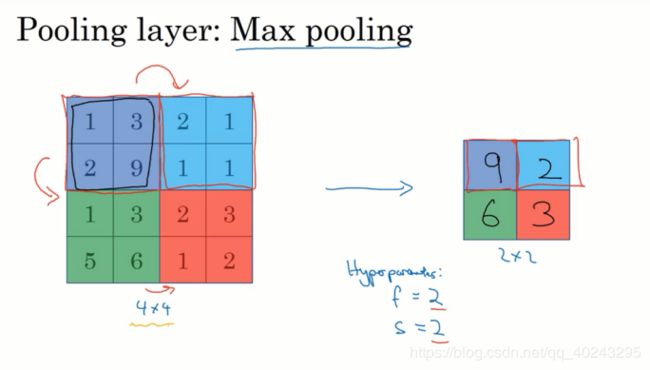
6.1 最大池化
假如输入是一个4x4矩阵,执行最大池化输出的是一个2x2矩阵
执行过程:把4x4输入拆分成不同的区域(图中用不同颜色标记4个区域),对于2x2的输出,输出的每个元素都是其对应颜色区域中的最大元素值。
这就像应用了一个规模为2X2,步长为2的过滤器,这就是最大池化的超级参数。
数字大意味着可能提取了某些特定特征,左上象限具有这个特征,其可能是一个垂直边缘;右上象限并不存在这个特征。
最大化操作的功能就是只要在任何一个象限内提取到某个特征,它就会保留在最大池化的输出里。最大化运算的实际作用就是如果在过滤器中提取到某个特征,那么就保留其最大值。如果没有提取到这个特征,其区域内最大值也是很小的,
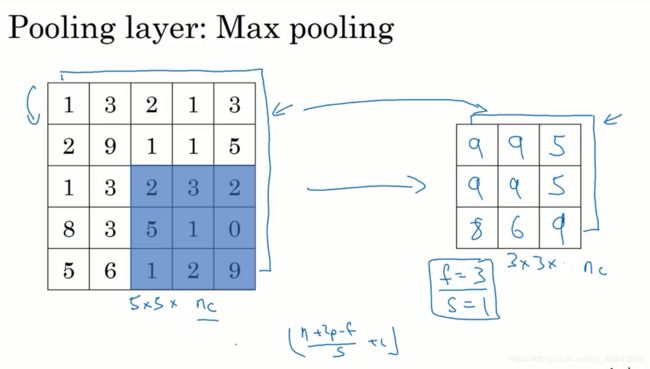
卷积层输出大小的公式,同样适用于池化层
6.2 平均池化(不太常用)
6.3 超级参数
池化的超级参数包括过滤器的大小f和步长s,常用参数是f=2,s=2,其效果相当于高度和宽度缩减一半,其他参数就要看你使用的是最大池化还是平均池化。它有一组超级参数,但是并没有参数需要学习,一旦f和s确定,它就是一个固定运算。
注意:池化过程中没有需要学习的参数,执行反向传播时,反向传播没有参数适用于最大池化;最大池化知识计算神经网络某一层的静态属性。
七、卷积神经网络示例
7.1 示例的构建过程详述
识别RGB图中的数字,输入是32x32x3,第一层过滤器大小是5x5,步长是1,padding是0,过滤器个数是6个,那么输出是28x28x6,增加偏差,应用非线性函数后输出,将这一层标记为CONV1;
然后构建一个池化层,选择最大池化,参数f=2,s=2(表示层的高度和宽度会减少一半)因此变为了14x14,通道数量保持不变,最终输出的为14x14x6,将该输出标记为POOL1;
在文献中卷积的分类有两种,这与所谓层的划分存在一致性,一类卷积是一个卷积层和一个池化层一起作为一层,这就是神经网络的Layer1,另一类卷积是吧卷积层作为一层,而池化层单独作为一层,人们在计算神经网络有多少层,通常只是统计具有权值和参数的层。因为池化层没有权重和参数,只有一些超级参数,这里我们把CONV1和POOL1共同作为一个卷积,并标记为Layer1。
此时Layer1的输出为14x14x6。
再构建一个卷积层,过滤器大小是5x5,步长是1,有16个过滤器,最后输出的是10x10x16的矩阵,记为CONV2;
然后做最大池化,超级参数f=2,s=2,结果是5x5x16,记为POOL2。
CONV2与POOL2组成一个卷积,记为Layer2。
5x5x16=400个元素,将POOL2平整化为一个大小为400的一维向量,将整平化的结果想象成一个神经元集合,然后利用这400个单元构建下一层,下一层含有个120个单元,这就是我们第一个全连接层,标记为FC3。
因为这400个单元与120个单元每一个相连接,这就是全连接层。这是一个标准的神经网络,它在120x400的维度上具有一个权重矩阵w[3],最后输出120个维度。
然后我们对这120个单元再添加一个全连接层,假设FC4有84个单元,用这84个单元填充一个softmax单元,其有10个输出(功能是识别0—9的10个数字)。
超级参数尽量采用文献中别人使用过的参数,这样效果比较好。
另外一种模型是一个或多个卷积层后面跟随一个池化层,然后一个或多个卷积层后面再跟随一个池化层,然后后面再跟几个全连接层。最后是softmax,这是神经网络的另一种常见模式。
7.2 示例中激活值的形状,大小,参数数量
输入层:32x32x3=3072,输入层没有参数
注意:
(1)池化层和最大池化层没有参数,
(2)卷积层的参数相对较少
(3)大多数参数存在于神经网络的全连接层,随着神经网络的加深,激活值会逐渐变小,若激活值下降太快,也会影响网络性能。
许多计算机视觉研究正在探索如何把这些基本模块(卷积层,池化层,全连接层)整合起来,构建高效的神经网络。
5x5=25,25+偏移量1=26个参数,26x8=208
5x5=25,25+偏移量1=26个参数,26x16=416
全连接层:400x120+1=48001
120x84+1=10081
84x10+1=841
八. 为什么使用卷积?
与只使用连接层相比,卷积层的两个主要优势在于参数共享和稀疏连接,假设有一张32x32x3维度的照片,用6个5x5的过滤器,输出的维度为28x28x6,32x32x3=3072,28x28x6=4704,我们构建一个神经网络,其中一层含有3072个单元,下一层含有4074个单元,,两层中的每个神经元彼此相连,然后计算权重矩阵,它等于3072x4704越等于1400万。因此要训练的参数很多,如果图片更大,权重矩阵就会变得非常大。
卷积层的参数数量:每个过滤器是5x5的,再加上偏差,因此每个过滤器有25+1=26个参数,一共6个过滤器,参数共计26x6=156个,参数数量还是很少的。
卷积网络映射参数少有两个原因:参数分享与稀疏连接。
8.1 参数共享
特征检测如垂直检测,如果其适用于某一区域,则它也可能适用于图片的其他区域,换而言之,就是你用一个3
x3的过滤器检测垂直边缘,那么图片左上角区域,以及旁边的各个区域都可以使用这个3x3的过滤器,每个特征检测器以及输出,都可以在输入图片的不同区域用使用相同的参数卷积,以便提取垂直边缘或其他特征。
整张照片共享一个特征检测器。提取效果也很好
8.2 稀疏连接
例如输出矩阵中的的第一个元素0,它只依赖输入中左上角3x3的单元格,即此0只与36个输入特征中的9个相连接。
神经网络可以通过参数分享,稀疏连接这两种机制减少参数。并且卷积神经网络善于捕捉平移不变。