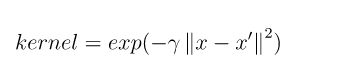scikit-learn代码实现SVM分类与SVR回归以及调参

分类

二分类：

from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
import mglearn.datasets
import matplotlib.pyplot as plt
#forge数据集是一个二维二分类数据集
X,y=mglearn.tools.make_handcrafted_dataset()
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2, random_state=33)
svm=SVC(kernel='rbf',C=10,gamma=0.1,probability=True).fit(X_train,y_train)

print(svm.predict(X_test))
#输出分类概率
print(svm.predict_proba(X_test))
print(svm.score(X_test,y_test))

[0 0 1 1 1 0]
[[0.91919503 0.08080497]
 [0.94703815 0.05296185]
 [0.04718756 0.95281244]
 [0.08991918 0.91008082]
 [0.18789225 0.81210775]
 [0.83350967 0.16649033]]
0.6666666666666666

多分类：

用的是鸢尾花数据集，其实代码和分类差不多

from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
import mglearn.datasets
from sklearn.datasets import load_iris
lr=load_iris()
X_train,X_test,y_train,y_test=train_test_split(lr.data,lr.target,test_size=0.2, random_state=33)
svm=SVC(kernel='rbf',C=10,gamma=0.1,probability=True).fit(X_train,y_train)

print(svm.predict(X_test))
#输出分类概率
print(svm.predict_proba(X_test))
print(svm.score(X_test,y_test))

[1 1 0 1 2 2 0 0 2 2 2 0 2 1 2 1 1 0 1 2 0 0 2 0 2 1 1 1 2 2]
[[0.00854955 0.97805528 0.01339518]
 [0.02046015 0.96924699 0.01029286]
 [0.95821345 0.02958702 0.01219953]
 [0.01262418 0.9436578  0.04371802]
 [0.01150194 0.21819026 0.7703078 ]
 [0.01106185 0.0025207  0.98641745]
 [0.93603376 0.04933543 0.01463081]
 [0.97333858 0.01668576 0.00997566]
 [0.01176501 0.10464775 0.88358724]
 [0.01189284 0.01007565 0.97803151]
 [0.01141951 0.0055538  0.98302669]
 [0.96745325 0.01936203 0.01318472]
 [0.01085658 0.0074639  0.98167952]
 [0.00991103 0.934642   0.05544697]
 [0.01539224 0.07365073 0.91095703]
 [0.01314571 0.9801558  0.00669849]
 [0.01167736 0.56576966 0.42255298]
 [0.97030247 0.01935948 0.01033805]
 [0.01612402 0.9036916  0.08018438]
 [0.01584532 0.03144821 0.95270647]
 [0.96485254 0.02414839 0.01099907]
 [0.95276015 0.03287629 0.01436357]
 [0.00943625 0.00639159 0.98417216]
 [0.96755483 0.02137253 0.01107264]
 [0.00979122 0.52403131 0.46617748]
 [0.01150947 0.57310996 0.41538057]
 [0.01065238 0.95469906 0.03464856]
 [0.01084855 0.98409152 0.00505992]
 [0.0121375  0.12769585 0.86016666]
 [0.01086478 0.25277848 0.73635675]]
0.9333333333333333

 

回归

回归的调参和分类是一样的。

# 导入库
import numpy as np  # numpy库
from sklearn.linear_model import BayesianRidge, LinearRegression, ElasticNet  # 批量导入要实现的回归算法
from sklearn.svm import SVR  # SVM中的回归算法
from sklearn.ensemble.gradient_boosting import GradientBoostingRegressor  # 集成算法
from sklearn.model_selection import cross_val_score  # 交叉检验
from sklearn.metrics import explained_variance_score, mean_absolute_error, mean_squared_error, r2_score  # 批量导入指标算法
import pandas as pd  # 导入pandas
import matplotlib.pyplot as plt  # 导入图形展示库
# 数据准备
raw_data = np.loadtxt('regression.txt')  # 读取数据文件
X = raw_data[:, :-1]  # 分割自变量
y = raw_data[:, -1]  # 分割因变量
# 训练回归模型
n_folds = 6  # 设置交叉检验的次数
model_br = BayesianRidge()  # 建立贝叶斯岭回归模型对象
model_lr = LinearRegression()  # 建立普通线性回归模型对象
model_etc = ElasticNet()  # 建立弹性网络回归模型对象
model_svr = SVR()  # 建立支持向量机回归模型对象
model_gbr = GradientBoostingRegressor()  # 建立梯度增强回归模型对象
model_names = ['BayesianRidge', 'LinearRegression', 'ElasticNet', 'SVR', 'GBR']  # 不同模型的名称列表
model_dic = [model_br, model_lr, model_etc, model_svr, model_gbr]  # 不同回归模型对象的集合
cv_score_list = []  # 交叉检验结果列表
pre_y_list = []  # 各个回归模型预测的y值列表
for model in model_dic:  # 读出每个回归模型对象
    scores = cross_val_score(model, X, y, cv=n_folds)  # 将每个回归模型导入交叉检验模型中做训练检验
    cv_score_list.append(scores)  # 将交叉检验结果存入结果列表
    pre_y_list.append(model.fit(X, y).predict(X))  # 将回归训练中得到的预测y存入列表
# 模型效果指标评估
n_samples, n_features = X.shape  # 总样本量,总特征数
#explained_variance_score:解释回归模型的方差得分，其值取值范围是[0,1]，越接近于1说明自变量越能解释因变量
    #的方差变化，值越小则说明效果越差。
#mean_absolute_error:平均绝对误差（Mean Absolute Error，MAE），用于评估预测结果和真实数据集的接近程度的程度
    #，其其值越小说明拟合效果越好。
#mean_squared_error:均方差（Mean squared error，MSE），该指标计算的是拟合数据和原始数据对应样本点的误差的
    #平方和的均值，其值越小说明拟合效果越好。
#r2_score:判定系数，其含义是也是解释回归模型的方差得分，其值取值范围是[0,1]，越接近于1说明自变量越能解释因
    #变量的方差变化，值越小则说明效果越差。
model_metrics_name = [explained_variance_score, mean_absolute_error, mean_squared_error, r2_score]  # 回归评估指标对象集
model_metrics_list = []  # 回归评估指标列表
for i in range(5):  # 循环每个模型索引
    tmp_list = []  # 每个内循环的临时结果列表
    for m in model_metrics_name:  # 循环每个指标对象
        tmp_score = m(y, pre_y_list[i])  # 计算每个回归指标结果
        tmp_list.append(tmp_score)  # 将结果存入每个内循环的临时结果列表
    model_metrics_list.append(tmp_list)  # 将结果存入回归评估指标列表
df1 = pd.DataFrame(cv_score_list, index=model_names)  # 建立交叉检验的数据框
df2 = pd.DataFrame(model_metrics_list, index=model_names, columns=['ev', 'mae', 'mse', 'r2'])  # 建立回归指标的数据框
print ('samples: %d \t features: %d' % (n_samples, n_features))  # 打印输出样本量和特征数量
print (70 * '-')  # 打印分隔线
print ('cross validation result:')  # 打印输出标题
print (df1)  # 打印输出交叉检验的数据框
print (70 * '-')  # 打印分隔线
print ('regression metrics:')  # 打印输出标题
print (df2)  # 打印输出回归指标的数据框
print (70 * '-')  # 打印分隔线
print ('short name \t full name')  # 打印输出缩写和全名标题
print ('ev \t explained_variance')
print ('mae \t mean_absolute_error')
print ('mse \t mean_squared_error')
print ('r2 \t r2')
print (70 * '-')  # 打印分隔线
# 模型效果可视化
plt.figure()  # 创建画布
plt.plot(np.arange(X.shape[0]), y, color='k', label='true y')  # 画出原始值的曲线
color_list = ['r', 'b', 'g', 'y', 'c']  # 颜色列表
linestyle_list = ['-', '.', 'o', 'v', '*']  # 样式列表
for i, pre_y in enumerate(pre_y_list):  # 读出通过回归模型预测得到的索引及结果
    plt.plot(np.arange(X.shape[0]), pre_y_list[i], color_list[i], label=model_names[i])  # 画出每条预测结果线
plt.title('regression result comparison')  # 标题
plt.legend(loc='upper right')  # 图例位置
plt.ylabel('real and predicted value')  # y轴标题
plt.show()  # 展示图像
# 模型应用
print ('regression prediction')
new_point_set = [[1.05393, 0., 8.14, 0., 0.538, 5.935, 29.3, 4.4986, 4., 307., 21., 386.85, 6.58],
                 [0.7842, 0., 8.14, 0., 0.538, 5.99, 81.7, 4.2579, 4., 307., 21., 386.75, 14.67],
                 [0.80271, 0., 8.14, 0., 0.538, 5.456, 36.6, 3.7965, 4., 307., 21., 288.99, 11.69],
                 [0.7258, 0., 8.14, 0., 0.538, 5.727, 69.5, 3.7965, 4., 307., 21., 390.95, 11.28]]  # 要预测的新数据集
for i, new_point in enumerate(new_point_set):  # 循环读出每个要预测的数据点
    new_point = np.array(new_point).reshape(1, 13)
    new_pre_y = model_gbr.predict(new_point)  # 使用GBR进行预测
    print ('predict for new point %d is:  %.2f' % (i + 1, new_pre_y))  # 打印输出每个数据点的预测信息

E:\anaconda\anacoda\python.exe E:/py文件/机器学习算法/SVC/SVR回归.py
samples: 506 	 features: 13
----------------------------------------------------------------------
cross validation result:
                         0         1         2         3         4         5
BayesianRidge     0.662422  0.677079  0.549702  0.776896 -0.139738 -0.024448
LinearRegression  0.642240  0.611521  0.514471  0.785033 -0.143673 -0.015390
ElasticNet        0.582476  0.603773  0.365912  0.625645  0.437122  0.200454
SVR              -0.000799 -0.004447 -1.224386 -0.663773 -0.122252 -1.374062
GBR               0.749808  0.806579  0.769107  0.865624  0.379249  0.555424
----------------------------------------------------------------------
regression metrics:
                        ev       mae        mse        r2
BayesianRidge     0.731143  3.319204  22.696772  0.731143
LinearRegression  0.740608  3.272945  21.897779  0.740608
ElasticNet        0.686094  3.592915  26.499828  0.686094
SVR               0.173548  5.447960  71.637552  0.151410
GBR               0.975126  1.151773   2.099835  0.975126
----------------------------------------------------------------------
short name 	 full name
ev 	 explained_variance
mae 	 mean_absolute_error
mse 	 mean_squared_error
r2 	 r2
----------------------------------------------------------------------
regression prediction
predict for new point 1 is:  21.49
predict for new point 2 is:  16.84
predict for new point 3 is:  19.50
predict for new point 4 is:  19.16

Process finished with exit code 0

 

调参

sklearn.svm.SVC(C=1.0,kernel='rbf', degree=3, gamma='auto',coef0=0.0,shrinking=True,probability=False,tol=0.001,cache_size=200, class_weight=None,verbose=False,max_iter=-1,decision_function_shape=None,random_state=None)

下面部分引用自https://blog.csdn.net/HHTNAN/article/details/79500003 

参数：

l C：C-SVC的惩罚参数C?默认值是1.0

C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

l kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’

　　0 – 线性核函数：u’v                           kernel=‘linear’

　　1 – 多项式核函数：(gamma*u’*v + coef0)^degree kernel=‘poly’

　　2 – 径向基核函数：exp(-gamma|u-v|^2)          kernel=‘rbf’

　　3 – sigmod核函数：tanh(gamma*u’*v + coef0)    kernel=‘sigmod’

l degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。

l gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features

l coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。

l probability ：是否采用概率估计？.默认为False

l shrinking ：是否采用shrinking heuristic方法，默认为true

l tol ：停止训练的误差值大小，默认为1e-3

l cache_size ：核函数cache缓存大小，默认为200

l class_weight ：类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)

l verbose ：允许冗余输出？

l max_iter ：最大迭代次数。-1为无限制。

l decision_function_shape ：‘ovo’, ‘ovr’ or None, default=None3

l random_state ：数据洗牌时的种子值，int值

主要调节的参数有：C、kernel、degree、gamma、coef0。

对上述参数的分析：

#参数shrinking中说的“启发式收缩”是指SMO算法中每一步选择变量的方式，可以参见周志华老师的《机器学习》第125页最上面的一段话，不过SMO算法讲的更详细的可以参见李航老师的《统计学习方法》。 参数decision_function_shape的意义可以参见周志华老师的《机器学习》第63页“多分类学习”部分

#decision_function_shape='ovo'时，为one v one分类问题，即将类别两两之间进行划分，用二分类的方法模拟多分类的结果。一对多法（one-versus-rest,简称1-v-r SVMs, OVR SVMs）训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类，这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类

#decision_function_shape='ovr'时，为one v rest分类问题，即一个类别与其他类别进行划分。一对一法（one-versus-one,简称1-v-1 SVMs, OVO SVMs, pairwise）。其做法是在任意两类样本之间设计一个SVM，因此k个类别的样本就需要设计k(k-1)/2个SVM。当对一个未知样本进行分类时，最后得票最多的类别即为该未知样本的类别。Libsvm中的多类分类就是根据这个方法实现的。 

#probability=True可以输出分类概率，不设置True会报错

#输出分类概率
print(svm.predict_proba(X_test))

# C是惩罚系数，即对误差的宽容度。c越高，说明越不能容忍出现误差,容易过拟合。C越小，容易欠拟合。C过大或过小，泛化能力变差 

#gamma是选择RBF函数作为kernel后，该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布，gamma越大，支持向量越少，gamma值越小，支持向量越多。支持向量的个数影响训练与预测的速度。 

#对各个核函数及其对应的参数进行分析：

1）对于线性核函数，没有专门需要设置的参数 

采用线性核kernel='linear’的效果和使用sklearn.svm.LinearSVC实现的效果一样，但采用线性核时速度较慢，特别是对于大数据集，推荐使用线性核时使用LinearSVC
2）对于多项式核函数，

有三个参数。-d用来设置多项式核函数的最高此项次数degree，也就是公式中的d，默认值是3。-g用来设置核函数中的gamma参数设置，也就是公式中的第一个r(gamma)，默认值是1/k（k是类别数）。-r用来设置核函数中的coef0，也就是公式中的第二个r，默认值是0。 
3）对于RBF核函数，有一个参数。

-g用来设置核函数中的gamma参数设置，也就是公式中的第一个r(gamma)，默认值是1/k（k是类别数）。 可以将gamma理解为支持向量影响区域半径的倒数，gamma越大，支持向量影响区域越小，决策边界倾向于只包含支持向量，模型复杂度高，容易过拟合；gamma越小，支持向量影响区域越大，决策边界倾向于光滑，模型复杂度低，容易欠拟合；
gamma的取值非常重要，即不能过小，也不能过大
4）对于sigmoid核函数，

有两个参数。-g用来设置核函数中的gamma参数设置，也就是公式中的第一个r(gamma)，默认值是1/k（k是类别数）。-r用来设置核函数中的coef0，也就是公式中的第二个r，默认值是0。

#关于核函数的选择问题：

SVM核函数的选择对于其性能的表现有至关重要的作用，尤其是针对那些线性不可分的数据，因此核函数的选择在SVM算法中就显得至关重要。

线性核，主要用于线性可分的情况，我们可以看到特征空间到输入空间的维度是一样的，其参数少速度快，对于线性可分数据，其分类效果很理想，因此我们通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的

多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，但是多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。

高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。

采用sigmoid核函数，支持向量机实现的就是一种多层神经网络。
因此，在选用核函数的时候，如果我们对我们的数据有一定的先验知识，就利用先验来选择符合数据分布的核函数；如果不知道的话，通常使用交叉验证的方法，来试用不同的核函数，误差最下的即为效果最好的核函数，或者也可以将多个核函数结合起来，形成混合核函数。在吴恩达的课上，也曾经给出过一系列的选择核函数的方法：

如果特征的数量大到和样本数量差不多，则选用LR或者线性核的SVM；
如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；
如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况
本人认为：样本数量相对于特征数偏少时，容易线性可分；比如说2*2，那么两个维度，两个样本，线性可分就非常简单；如果另外一个极端，即线性可分的概率就会很低；一种方法采用高斯核，另外一种方法增加特征；说白了本质上就是增加维度；缩小特征数与样本数之间的差距，来达到线性可分 ；

再来看看：

sklearn.svm包中的SVC(kernel="linear")和LinearSVC的区别

1、LinearSVC使用的是平方hinge loss，SVC使用的是绝对值hinge loss
（我们知道，绝对值hinge loss是非凸的，因而你不能用GD去优化，而平方hinge loss可以）

2、LinearSVC使用的是One-vs-All（也成One-vs-Rest）的优化方法，而SVC使用的是One-vs-One

3、对于多分类问题，如果分类的数量是N，则LinearSVC适合N模型，而SVC适合N(N-1)/2模型

4、LinearSVC基于liblinear，罚函数是对截矩进行惩罚；SVC基于libsvm，罚函数不是对截矩进行惩罚。

5、我们知道SVM解决问题时，问题是分为线性可分和线性不可分问题的，liblinear对线性可分问题做了优化，故在大量数据上收敛速度比libsvm快
一句话，大规模线性可分问题上LinearSVC更快,所以，整体而言，如果你决定使用线性SVM，就使用LinearSVC，但如果你要是用其他核的SVM，就只能使用SVC。

同样，LinearSVR和SVR也是这个道理

调参

此类支持密集和稀疏输入，并且多类支持根据one-vs-the-rest方案处理。

Sklearn.svm.LinearSVC(penalty=’l2’, loss=’squared_hinge’, dual=True, tol=0.0001, C=1.0, multi_class=’ovr’,fit_intercept=True, intercept_scaling=1, class_weight=None, verbose=0, random_state=None, max_iter=1000)

penalty : string, ‘l1’ or ‘l2’ (default=’l2’)

指定惩罚中使用的规范。 'l2'惩罚是SVC中使用的标准。 'l1'导致稀疏的coef_向量。

loss : string, ‘hinge’ or ‘squared_hinge’ (default=’squared_hinge’)

指定损失函数。 “hinge”是标准的SVM损失（例如由SVC类使用），而“squared_hinge”是hinge损失的平方。

dual : bool, (default=True)

选择算法以解决双优化或原始优化问题。 当n_samples> n_features时，首选dual = False。

tol : float, optional (default=1e-4)

公差停止标准

C : float, optional (default=1.0)

错误项的惩罚参数

multi_class : string, ‘ovr’ or ‘crammer_singer’ (default=’ovr’)

如果y包含两个以上的类，则确定多类策略。 “ovr”训练n_classes one-vs-rest分类器，而“crammer_singer”优化所有类的联合目标。 虽然crammer_singer在理论上是有趣的，因为它是一致的，但它在实践中很少使用，因为它很少能够提高准确性并且计算成本更高。 如果选择“crammer_singer”，则将忽略选项loss，penalty和dual。

fit_intercept : boolean, optional (default=True)

是否计算此模型的截距。 如果设置为false，则不会在计算中使用截距（即，预期数据已经居中）。

intercept_scaling : float, optional (default=1)

当self.fit_intercept为True时，实例向量x变为[x，self.intercept_scaling]，即具有等于intercept_scaling的常量值的“合成”特征被附加到实例向量。 截距变为intercept_scaling *合成特征权重注意！ 合成特征权重与所有其他特征一样经受l1 / l2正则化。 为了减小正则化对合成特征权重（并因此对截距）的影响，必须增加intercept_scaling。

class_weight : {dict, ‘balanced’}, optional

将类i的参数C设置为SVC的class_weight [i] * C. 如果没有给出，所有课程都应该有一个重量。 “平衡”模式使用y的值自动调整与输入数据中的类频率成反比的权重，如n_samples /（n_classes * np.bincount（y））

verbose : int, (default=0)

启用详细输出。 请注意，此设置利用liblinear中的每进程运行时设置，如果启用，可能无法在多线程上下文中正常工作。

random_state : int, RandomState instance or None, optional (default=None)

在随机数据混洗时使用的伪随机数生成器的种子。 如果是int，则random_state是随机数生成器使用的种子; 如果是RandomState实例，则random_state是随机数生成器; 如果为None，则随机数生成器是np.random使用的RandomState实例。

max_iter : int, (default=1000)

要运行的最大迭代次数。
原文出自：https://blog.csdn.net/ustbclearwang/article/details/81236732

对象：
coef_:各特征的系数（重要性）。
intercept_:截距的大小（常数值）

再看看：NUSVC

class sklearn.svm.NuSVC(nu=0.5, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', random_state=None))

SVC和 NuSVC差不多，区别仅仅在于对损失的度量方式不同，什么特殊场景需要使用NuSVC分类 和 NuSVR 回归呢？如果我们对训练集训练的错误率或者说支持向量的百分比有要求的时候，可以选择NuSVC分类 和 NuSVR 。它们有一个参数来控制这个百分比。

调参

nu:训练误差部分的上限和支持向量部分的下限，取值在（0，1）之间，默认是0.5
kernel:核函数，核函数是用来将非线性问题转化为线性问题的一种方法，默认是“rbf”核函数，常用的核函数有以下几种：

表示

解释

linear

线性核函数

poly

多项式核函数

rbf

高斯核函数

sigmod

sigmod核函数

precomputed

自定义核函数

关于不同核函数之间的区别，可以参考这篇文章：https://blog.csdn.net/batuwuhanpei/article/details/52354822

degree:当核函数是多项式核函数的时候，用来控制函数的最高次数。（多项式核函数是将低维的输入空间映射到高维的特征空间）
gamma:核函数系数，默认是“auto”，即特征维度的倒数。
coef0:核函数常数值(y=kx+b中的b值)，只有‘poly’和‘sigmoid’核函数有，默认值是0。
max_iter:最大迭代次数，默认值是-1，即没有限制。
probability:是否使用概率估计，默认是False。
decision_function_shape:与'multi_class'参数含义类似。
cache_size:缓冲大小，用来限制计算量大小，默认是200M。

对象
support_:以数组的形式返回支持向量的索引。
support_vectors_:返回支持向量。
n_support_:每个类别支持向量的个数。
dual_coef_:支持向量系数。
coef_:每个特征系数（重要性），只有核函数是LinearSVC的时候可用。
intercept_:截距值（常数值）。