数据结构------堆(二、堆的实现)
一、堆的定义
我们知道堆是一个树形结构,其实堆的底层是一棵完全二叉树。而完全二叉树是一层一层按照进入的顺序排成的。按照这个特性,我们可以用数组来按照完全二叉树实现堆。
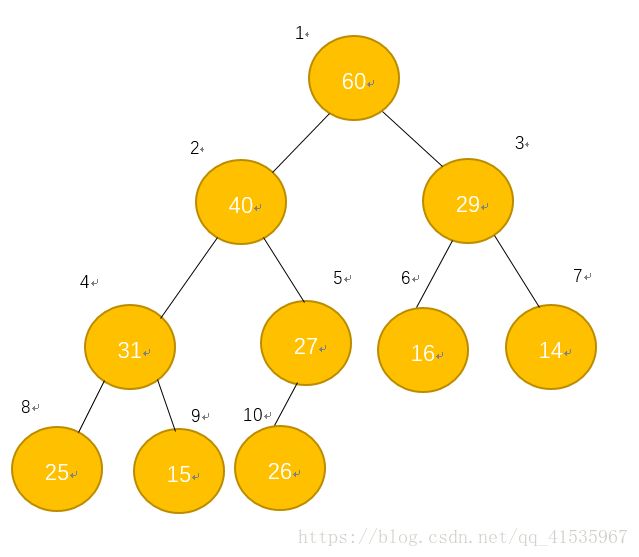
上面的图片就是一个完全二叉树,也是一个最大堆。而最大堆有一个性质:每一个节点的值都小于它父节点的值。我们也可以从上面的图片中看出来。但是需要注意的是,每一个节点的值的大小与它所处的深度没有必然的联系。因为我们可以看到第三层的六号和七号节点都小于处于最后一层的八号和十号节点。
我们如果将这个最大堆存入数组中,就需要按照索引顺序存入:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 60 | 40 | 29 | 31 | 27 | 16 | 14 | 25 | 15 | 26 |
我们可以很容易的根据任意一个节点的索引(除去根节点)找到它的父节点的索引,如果当前节点的索引为index,那么:
当前节点的父节点 = index / 2(这里我们将结果取整)。
我们也可以很容易的找到它左右子节点的索引:
当前节点的左子节点 = index * 2
当前节点的右子节点 = index * 2 + 1。
但是现在就会出现一个问题,索引为0的空间空出来了。不过这也不是一个太大的问题,因为我们知道,在循环队列或者在一个拥有虚拟头结点的链表中都会有一个空间不存放数据,但如果我们不想空出一个空间,那我们的数据就会变成:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 60 | 40 | 29 | 31 | 27 | 16 | 14 | 25 | 15 | 26 |
虽然数据的位置变了,但是我们的公式也只是发生了很小的改变:
当前节点的父节点 = (index - 1) / 2
当前节点的左子节点 = index * 2 + 1
当前节点的左子节点 = index * 2 + 2
二、如何去实现一个堆
下面,我们来用代码实现一个堆。
首先,我先自定义了一个动态数组,因为自定义的动态数组可以在其类中增加一些其他的辅助方法,而且因为我们要将最大堆在数组中存放。然后定义一个最大堆类,类名叫作MaxHeap,然后将动态数组实例化,之后我们就可以调用动态数组中的方法来更容易的实现堆的逻辑。
public class MaxHeap> {//因为堆中元素需要比较,所以泛型E实现Comparable接口
private Array data;
//如果传入一个参数,动态数组就会按传入的参数规定数组的初始大小
public MaxHeap(int capacity) {
data = new Array<>(capacity);
}
//如果不传入参数,动态数组规定默认大小
public MaxHeap() {
data = new Array<>();
}
//获得堆中的元素个数
public int getSize() {
return data.getSize();
}
//判断堆中是否为空
public boolean isEmpty() {
return data.isEmpty();
} 然后我们可以通过刚才的通过当前索引查找父节点和子节点索引的公式写出代码:
//根据堆中元素的索引获得其父亲节点的索引
private int parent(int index) {
if (index == 0)
throw new IllegalArgumentException("Index-0 doesn't have parent");
return (index - 1) / 2;
}
//根据堆中元素的索引获得其左孩子节点的索引
private int leftChild(int index) {
return index * 2 + 1;
}
//根据堆中元素的索引获得其右孩子节点的索引
private int rightChild(int index) {
return index * 2 + 2;
}private void siftUp(int k) {
//如果当前索引所对应的元素的值大于其父亲节点所对应的值,两个元素交换位置
while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
data.swap(parent(k), k);
k = parent(k);
}
}这个方法可以称为“上浮”,因为如果插入的节点的值大于它的父节点的值,那么两个节点就交换位置,相当于是一个上浮的操作。
之后我们就可以定义一个添加节点的方法,在添加节点之后再加上siftUp操作就可以实现最大堆的定义:
//向堆中添加元素
public void add(E e) {
data.addLast(e);
siftUp(data.getSize() - 1);
}//查看堆中的最大元素
public E findMax() {
if (data.getSize() == 0)
throw new IllegalArgumentException("Cannot findMax when heap is empty.");
return data.get(0);
}private void siftDown(int k) {
//判断左孩子是否大于数组的大小
while (leftChild(k) < data.getSize()) {
int j = leftChild(k);
//如果该节点还有右孩子而且右孩子大于左孩子那么将右孩子与该节点互换
if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0)
j = rightChild(k);
if (data.get(k).compareTo(data.get(j)) >= 0)
break;
data.swap(j, k);
k = j;
}
}这个方法的作用就是如果当前节点小于它的子节点,就与子节点中最大的节点互换位置,所以这个方法也可以叫做“下沉”。
之后我们就可以取出堆中最大的元素了:
//取出堆中的最大元素
public E extractMax() {
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}这个取出最大元素的方法是:先将最大的节点与最后一个节点交换位置,然后再进行“下沉”操作,这样就可以将取出最大值之后的最大堆构建出来了。