数据结构——内部排序算法比较(冒泡排序、直接插入排序、简单选择排序、希尔排序、快速排序、堆排序、归并排序)
[运行环境]
Codeblocks
程序语言:C语言
为了便于算法描述,扩展了C++语言的引用调用的参数传递方法。用&打头的参数即为引用参数,所以在codeblocks中,需要将主程序修改为cpp后缀才能使用引用参数。
[问题描述]
在教科书中,各种内部排序算法的时间复杂度分析结果只给出了算法执行时间的阶,或大概执行时间。试通过随机数据比较各算法的关键字比较次数和关键字移动次数,以取得直观感受。
[基本要求]
- 对以下6种常用的内部排序算法进行比较:起泡排序,直接插入排序,简单选择排序,快速排序,希尔排序,堆排序。
- 待排序表的表长不小于100;其中的数据要用伪随机数产生程序产生;至少要用5组不同的输入数据作比较;比较的指标为有关键字参加的比较次数和关键字的移动次数(关键字交换计为3次移动)。
- 最后要对结果作出简单分析,包括对各组数据得出结果波动大小的解释。
[测试数据]
由随机数产生器生成。
[实现提示]
主要工作是设法在已知算法中的适当位置插入对关键字的比较次数和移动次数的计数操作。程序还可以考虑几组数据的典型性,如,正序、逆序和不同程度的乱序。注意采用分块调试的方法。
[选做内容]
归并排序
1.需求分析
- 输入的形式和输入值的范围:
数据用伪随机数产生程序产生,输入数据的表长不小于100,输入字符的ASCII范围在97-122之间,即大写字母。 - 输出的形式:
输出各类排序算法关键字参加的比较次数和关键字的移动次数(关键字交换计为3次移动)的数据。 - 程序所能达到的功能:
通过随机数据比较各算法的关键字比较次数和关键字移动次数,取得对各种排序算法性能的直观感受。 - 测试数据:
用户输入最短表长,并选择进行哪种(正序,逆序,无序)排序算法测试。
输出:原始字符串,各种排列算法测试的结果,排列后的字符串,字符串的长度。
2.概要设计
程序利用顺序表和堆结构进行排序算法测试。
主程序利用随机数种子创建随机数表长度,根据用户的选择创建正序表、逆序表和无序表,然后进行排序算法测试,输出测试结果。
主要函数功能及调用关系:
Copy_L(SqList &Lin, SqList &Lo, int Length):函数复制顺序表,用于不用的排序算法。
Status Print(SqList &L):函数打印顺序表内容。
void BubbleSort(SqList &L, int &bubble_c, int &bubble_s):冒泡排序算法
void InsertSort(SqList &L, int &insert_c, int &insert_s):直接插入排序算法
void SelectEasy(SqList &L, int &Easy_c, int &Easy_s):简单选择排序算法
void ShellSort(SqList &L, int d[], int t, int &shell_c, int &shell_s): 希尔排序算法,其调用ShellInsert()函数进行一趟希尔排序
void QuickSort(SqList &L, int &quick_c, int &quick_s):快速排序算法,其调用QSort()进行快速排序,QSort()中调用Partition()对数据进行一次划分,输出枢轴值
void HeapSort(SqList &L, int &Heap_c, int &Heap_s):堆排序算法,其调用建堆函数MakeHeap()和删除堆顶结点函数RemoveFirstHeap()
void MergeSort(SqList &L, int &merge_c, int &merge_s):归并排序算法,调用MSort()进行递归归并,MSort()调用Merge()进行一次归并排序
3.详细设计
//顺序表结构定义
typedef char KeyType;
typedef struct {
KeyType key; //记录中的关键字类型元素
} RcdType;
typedef struct {
RcdType * rcd; //存储空间的基址
int length; //当前长度,不包括下标为0的元素
int size; //存储容量
int increment; //扩容容量
} SqList; //顺序表
//堆数据结构类型定义:
typedef struct {
RcdType *rcd; //堆基址,0号单元闲置
int n; //堆长度
int size; //堆容量
int tag; //小顶堆和大顶堆标志,0->小,1->大
int (*prior)(KeyType, KeyType); //函数指针,用于关键字的优化
} Heap; //堆
调用关系图
4.调试分析
调式过程中遇到的问题:
- 调试过程中遇到不少问题,一般通过查看报错信息解决。
- 利用printf输出语句检查变量的变化,发现错误的逻辑位置
- 在主程序while循环中没有调用顺序表的Destroy()函数,导致重新进入while循环时,顺序表非空,元素插入非空顺序表出错。
- 在删除堆顶结点的算法实现中,没有在每次交换堆顶元素与堆尾元素后,将堆长度减1,导致筛选出错。
算法的时空分析(默认复杂度为最坏情况):
| 排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 冒泡排序 | O(n^2) | O(1) | 稳定 |
| 直接插入排序 | O(n^2) | O(1) | 稳定 |
| 简单选择排序 | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | 尚难准确分析 | O(1) | 不稳定 |
| 快速排序 | O(n^2) | O(n) | 不稳定 |
| 堆排序 | O(nlogn) | O(1) | 不稳定 |
| 归并排序 | O(nlogn) | O(n) | 稳定 |
经验与体会:
事先确定好整体程序的框架,构思好所要实现的数据结构和函数模块,可以尽量避免在实现程序过程中出现的前后矛盾问题。
5.用户使用说明
用户根据界面中的提示输入顺序表长度最小值,然后选择功能(输入1,2,3),比如1表示执行随机无序顺序表的排序算法比较并输出结果,用户可以多次输入,对排序结果进行分析比较,输入1,2,3之外的数据,程序退出。(每次进入程序,顺序表长度为不小于100的整数)
6.测试结果
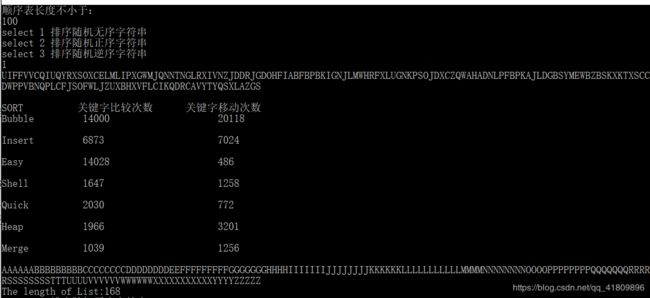
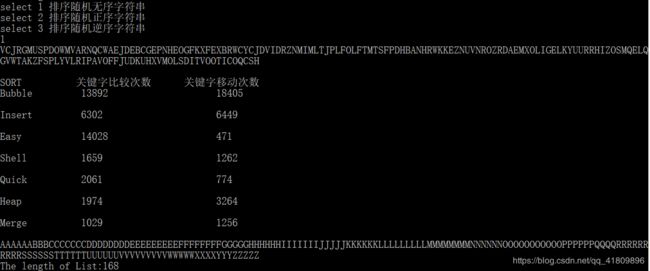
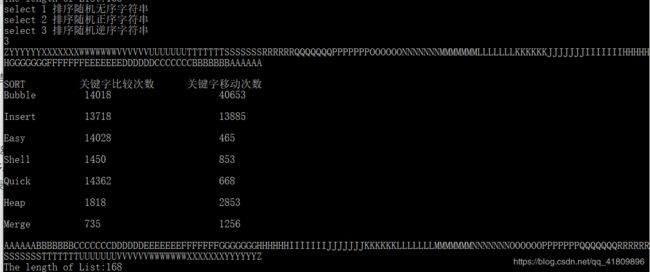
输入长度最小值100,然后连续输入5次1:
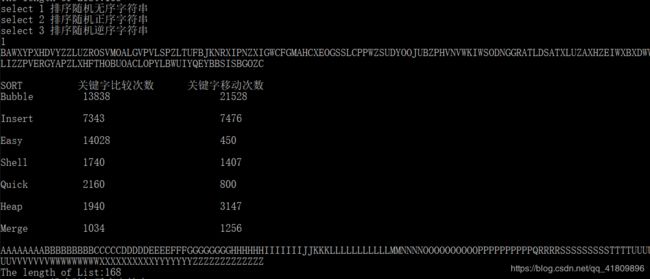
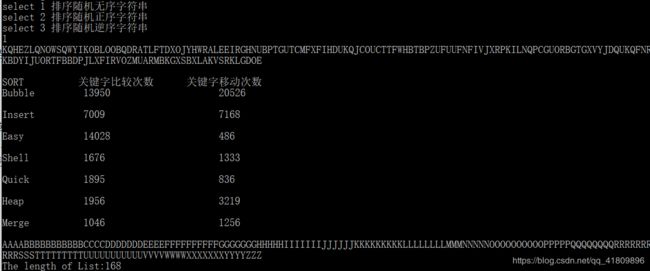
然后再输入2和3查看正序与逆序排序算法测试结果:
- 数据表明,简单选择排序中关键字的比较次数不会波动,因为无论数据如何变化,只要总数不变,简单选择排序都要执行循环中的比较语句。本程序冒泡排序是对传统算法的改进,如果在一趟比较中,未进行任何关键字的交换,则顺序表已经有序,退出循环,跟传统算法比较,减少了比较的次数(传统算法的比较次数应该跟简单选择排序算法一致)
- 希尔排序和快排中关键字的移动次数波动较大。是由于这两种排序进行数据之间交换位置的动作较大,因此当数据较混乱和较整齐时,移动次数的结果会相差较大。
- 希尔排序是直接插入排序的一种改进算法,算法的关键字比较次数和交换次数都显著减少。因为希尔排序前面各趟的调整可以看作是最后一趟的预处理,比只做一次直接插入排序效率更高。
- 堆排序关键字的移动次数不变,是因为在每次归并排序中,无论要归并的子序列是什么,都要将所有子序列的元素复制到新的序列上,每个关键字都移动一次。
- 对正序字符串和逆序字符串进行快速排序,关键字移动次数和比较次数都一样,且比较次数较多,这是因为在执行划分算法的时候,每一次序列的0号元素都是最大或者是最小,序列中的每个元素都需要跟0号位置元素进行比较,因此快速排序算法在进行执行划分算法寻找枢轴的时候,序列的第一个元素太大或太小都会影响算法效率。
7.附录
-
公用头文件DS0.h:
//公用头文件
#include <conio.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <values.h>
#include "time.h"
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define IBFEASIBLE -1
#define OVERFLOW -2
#define MAXLEN 20
#define MAXSIZE 20
typedef int Status;
-
定义数据结构DS1.h:
//定义数据结构
#define LIST_INIT_SIZE 150 /*线性表存储空间的初始分配量*/
#define LISTINCREMENT 50 /*线性表存储空间的分配增量*/
typedef char KeyType;
typedef struct {
KeyType key; //记录中的关键字类型元素
} RcdType;
typedef struct {
RcdType * rcd; //存储空间的基址
int length; //当前长度,不包括下标为0的元素
int size; //存储容量
int increment; //扩容容量
} SqList; //顺序表
Status InitList(SqList &L){
L.rcd = (RcdType*)malloc(sizeof(RcdType)*(LIST_INIT_SIZE));
if(NULL == L.rcd)return OVERFLOW;
L.length=0;
L.size = LIST_INIT_SIZE;
L.increment = LISTINCREMENT;
return OK;
}
Status Destroy(SqList &L){
free(L.rcd);
L.rcd = NULL;
return OK;
}
Status Append(SqList &L, KeyType e){
RcdType *newbase;
//如果长度大于顺序表存储容量,进行扩容
if(L.length+1 >= L.size){
newbase = (RcdType*)realloc(L.rcd, (L.size+L.increment)*
sizeof(RcdType));
if(NULL==newbase)return OVERFLOW;
L.rcd = newbase;
L.size += L.increment;
}
L.rcd[L.length+1].key=e;
L.length++;
return OK;
}
Status Print(SqList &L){
int i;
for(i=1; i<L.length+1; i++){
printf("%c",L.rcd[i].key);
}
printf("\n");
}
typedef struct {
RcdType *rcd; //堆基址,0号单元闲置
int n; //堆长度
int size; //堆容量
int tag; //小顶堆和大顶堆标志,0->小,1->大
int (*prior)(KeyType, KeyType); //函数指针,用于关键字的优化
} Heap; //堆
Status greatPrior(KeyType x,KeyType y){ //大顶堆优先函数
return x>=y;
}
Status swapHeapElem(Heap &H, int a, int b){
//堆元素交换位置
if(a<=0 || a>H.n || b<=0 || b>H.n)return ERROR;
RcdType temp;
temp = H.rcd[a];
H.rcd[a] = H.rcd[b];
H.rcd[b] = temp;
return OK;
}
void ShiftDown(Heap &H, int pos, int &Heap_c, int &Heap_s){
//堆的筛选操作
//对堆中位置为pos的结点做筛选,将以POS为根的子树调整为子堆
int c,rc;
while(pos <= H.n/2){ //若pos结点为叶子结点,循环结束
c = pos*2; //c为pos结点的左孩子位置
rc = pos*2+1; //rc为pos结点的右孩子位置
Heap_c++;//关键字比较一次
if(rc <= H.n && H.prior(H.rcd[rc].key, H.rcd[c].key) ){
c = rc; //c为pos结点的左右孩子中较优先者的位置
}
Heap_c++;//关键字比较一次
if(H.prior(H.rcd[pos].key, H.rcd[c].key)){
return; //若pos结点较优先,则筛选结束
}
swapHeapElem(H, pos, c); //否则pos和较优先者c交换位置
Heap_s += 3;//关键字交换一次
pos = c; //继续向下调整
}
}
void MakeHeap(Heap &H, RcdType *E, int n, int size, int tag,int (*prior)(KeyType, KeyType), int &Heap_c, int &Heap_s){
//用E建长度为n的堆H,容量为size,当tag为0或1时分别表示小顶堆或者大顶堆
//prior为优先函数
int i;
H.rcd = E; //E是堆的n个结点,0号单元闲置
H.n = n;
H.size = size;
H.tag = tag;
H.prior = prior;
for(i=n/2; i>0; i--){
ShiftDown(H, i, Heap_c, Heap_s); //对以i为根的子树进行筛选
}
}
Status RemoveFirstHeap(Heap &H, RcdType &e, int &Heap_c, int &Heap_s){
//删除堆顶结点
if(H.n<=0)return ERROR;
e = H.rcd[1]; //取出堆顶结点
swapHeapElem(H, 1, H.n); //交换堆顶与堆尾结点
Heap_s += 3;//关键字交换
H.n--; //堆长度减一
if(H.n>1)ShiftDown(H, 1, Heap_c, Heap_s); //从堆顶位置向下筛选,堆顶元素置为最大值
return OK;
}
-
排序算法DS2.h:
//排序算法
void BubbleSort(SqList &L, int &bubble_c, int &bubble_s){
//冒泡排序算法
int i,j;
RcdType temp;
int reg=1; //改进的冒泡排序中增加的reg变量,用于判断循环是否继续
for(i=L.length; i>1&® i--){
reg=0; //reg赋值为0
for(j=1; j<i; j++){
bubble_c++; //比较一次
if(L.rcd[j].key > L.rcd[j+1].key){
bubble_s += 3; //交换一次
temp = L.rcd[j];
L.rcd[j] = L.rcd[j+1];
L.rcd[j+1] = temp;
reg=1; //如果没有进入该for循环,则reg为0,最外层循环将结束
}
}
}
}
void InsertSort(SqList &L, int &insert_c, int &insert_s){
//直接插入排序
int i,j;
for(i=1; i<L.length; i++){
insert_c++; //比较一次
if(L.rcd[i+1].key < L.rcd[i].key){ //需要将L.elem[i+1]插入有序序列
L.rcd[0] = L.rcd[i+1]; //先将L.elem[i+1]保存在空闲的0号单元
insert_s++; //关键字移动一次
j=i+1;
do{
//循环将关键字后移,直到找到合适的位置进行0号元素的插入操作
j--;
L.rcd[j+1]=L.rcd[j];
insert_s++; //移动一次
insert_c++; //在while中将会比较一次
}while(L.rcd[0].key < L.rcd[j-1].key);
L.rcd[j] = L.rcd[0];
insert_s++; //移动一次
}
}
}
void SelectEasy(SqList &L, int &Easy_c, int &Easy_s){
//简单选择排序
int i,j,k;
RcdType temp;
for(i=1; i<L.length; i++){
for(j=i,k=i; j<L.length; j++){
Easy_c++;//比较一次
if(L.rcd[k].key > L.rcd[j+1].key){
k=j+1;//记录最小值下标
}
}
if(k!=i){
temp = L.rcd[i];
L.rcd[i] = L.rcd[k];
L.rcd[k] = temp;
Easy_s += 3;//关键字交换
}
}
}
void ShellInsert(SqList &L, int dk, int &shell_c, int &shell_s){
//一趟希尔排序算法
int i,j;
for(i=1; i<=L.length-dk; i++){
shell_c++;//比较一次
if(L.rcd[i+dk].key < L.rcd[i].key){ //需要将L.elem[i+1]插入有序序列
L.rcd[0] = L.rcd[i+dk]; //先将L.elem[i+1]保存在空闲的0号单元
shell_s++;//关键字移动一次
j=i+dk;
do{
//循环将关键字后移,直到找到合适的位置进行0号元素的插入操作
j -= dk;
L.rcd[j+dk]=L.rcd[j];
shell_s++;//移动一次
shell_c++;//while将会比较一次
}while(j-dk>0&&L.rcd[0].key < L.rcd[j-dk].key);
//(j-dk>0)注意数组越界问题
L.rcd[j] = L.rcd[0];
shell_s++;//移动一次
}
}
}
void ShellSort(SqList &L, int d[], int t, int &shell_c, int &shell_s){
//希尔排序
int k;
for(k=0; k<t; k++){
ShellInsert(L, d[k], shell_c, shell_s);
}
}
int Partition(RcdType rcd[], int low, int high, int &quick_c, int &quick_s){
//对子列elem进行一次划分,并返回返回枢轴应当所处的位置
//使得枢轴前的关键字均不大于它的关键字,枢轴之后的关键字均不小于它的关键字
rcd[0]=rcd[low]; //将默认枢轴移至0号位置
quick_s++;//关键字移动一次
while(low<high){
while(low<high && rcd[high].key
>= rcd[0].key){
--high;
quick_c++;//关键字进行比较一次
}
quick_c++;//容易忽略,退出循环前关键字比较一次
rcd[low]=rcd[high];
quick_s++;//关键字移动一次
while(low<high && rcd[low].key <= rcd[0].key){
quick_c++;//关键字进行比较一次
++low;
}
quick_c++;//容易忽略,退出循环前关键字比较一次
rcd[high]=rcd[low];
quick_s++;//关键字移动一次
}
rcd[low]=rcd[0];//当low等于high,枢轴的位置下标为low或high
quick_s++;//移动一次
return low;
}
void QSort(RcdType rcd[], int s, int t, int &quick_c, int &quick_s){
//快速排序
int pivotloc;
if(s<t){
pivotloc = Partition(rcd, s, t, quick_c, quick_s);
QSort(rcd, s, pivotloc-1, quick_c, quick_s);
QSort(rcd, pivotloc+1, t, quick_c, quick_s);
}
}
void QuickSort(SqList &L, int &quick_c, int &quick_s){
QSort(L.rcd, 1, L.length, quick_c, quick_s);
}
void HeapSort(SqList &L, int &Heap_c, int &Heap_s){
//堆排序
Heap H;
int i,j;
RcdType e;
MakeHeap(H, L.rcd, L.length, L.size, 1, greatPrior, Heap_c, Heap_s);//待排列建大顶堆
for(i=H.n; i>0; i--){
RemoveFirstHeap(H, e, Heap_c, Heap_s); //堆顶与堆尾结点交换,堆长度减一,筛选新的堆顶结点
L.rcd[i] = e; //给原来的顺序表重新赋值好排序后的元素
}
}
void Merge(RcdType SR[], RcdType TR[], int i, int m, int n, int &merge_c, int &merge_s){
//一次归并排序
//将相邻的有序区间SR[i.m]和SR[m+1.n]归并为有序的TR[i.n]
int k,j;
for(j=m+1,k=i; i<=m && j<=n; k++){
//将SR中记录按关键字从小到大地赋值到TR中
merge_c++; //关键字比较一次
if(SR[i].key<=SR[j].key){
merge_s++; //关键字移动一次
TR[k] = SR[i++];
}
else{
merge_s++; //关键字移动一次
TR[k] = SR[j++];
}
}
while(i<=m){
TR[k++] = SR[i++]; //将剩余的SR[i.m]复制到TR
merge_s++; //关键字移动一次
}
while(j<=n){
TR[k++] = SR[j++]; //将剩余的SR[m+1.n]复制到TR
merge_s++; //关键字移动一次
}
}
void MSort(RcdType R1[], RcdType R2[], int i, int s, int t, int &merge_c, int &merge_s){
//递归归并排序
//对R1归并排序,若i%2==1,则排序后的记录存入R2,否则存入R1
int m;
if(s==t){
if(1==i%2)R2[s] = R1[s];
}else{
m = (s+t)/2; //将区间平分为[s..m]和[m+1..t]
MSort(R1, R2, i+1, s, m, merge_c, merge_s); //对区间[s..m]递归
MSort(R1, R2, i+1, m+1, t, merge_c, merge_s); //对区间[m+1..t]递归
if(1==i%2){ //将R1[s..m]和R2[m+1..t]归并到R2[s..t]
Merge(R1, R2, s, m, t, merge_c, merge_s);
}
else //将R2[s..m]和R1[m+1..t]归并到R2[s..t]
Merge(R2, R1, s, m, t, merge_c, merge_s);
}
}
void MergeSort(SqList &L, int &merge_c, int &merge_s){
//对顺序表进行2-路归并排序
RcdType *R;
R = (RcdType*)malloc((L.length+1)*sizeof(RcdType)); //分配辅助空间
MSort(L.rcd, R, 0, 1, L.length, merge_c, merge_s); //对L进行归并排序
free(R);
}
-
程序主函数main.cpp:
#include <stdio.h>
#include <stdlib.h>
#include "DS0.h"
#include "DS1.h"
#include "DS2.h"
void Copy_L(SqList &Lin, SqList &Lo, int Length){
int i;
char c;
for(i=0; i<Length; i++){
c = Lin.rcd[i+1].key;
Append(Lo, c);
}
}
int main()
{
srand((unsigned)time(NULL));//随机数种子
int Length=0,i;
KeyType c;
SqList l,l2,l3,l4,l5,l6,l7;
Heap h;
int ListL=0;
printf("顺序表长度不小于:\n");
scanf("%d",&ListL);
Length = 0;
while(Length<=ListL){
Length += rand()%150;//产生数值小于50的随机栈元素个数
}
Length = 168;
int select=0;
int bubble_c=0,bubble_s=0;
int insert_c=0,insert_s=0;
int easy_c=0,easy_s=0;
int shell_c=0,shell_s=0;
int quick_c=0,quick_s=0;
int heap_c=0,heap_s=0;
int merge_c=0,merge_s=0;
do{
InitList(l); //随机序列顺序表
InitList(l2);InitList(l3);InitList(l4);InitList(l5);InitList(l6);InitList(l7);
printf("select 1 排序随机无序字符串\n");
printf("select 2 排序随机正序字符串\n");
printf("select 3 排序随机逆序字符串\n");
scanf("%d",&select);
switch (select){
case 1:
for(i=0; i<Length; i++){
c = 'A'+ rand()%26;
Append(l, c); //产生随机的大写字符串插入线性表
}
break;
case 2:
for(i=0; i<Length; i++){
c = 'A'+ i*1.0/Length*26;
Append(l, c); //产生正序的大写字符串插入线性表
}
break;
case 3:
for(i=0; i<Length; i++){
c = 'Z'- i*1.0/Length*25;
Append(l, c); //产生逆序的大写字符串插入线性表
}
break;
}
Copy_L(l, l2, Length);Copy_L(l, l3, Length);Copy_L(l, l4, Length);Copy_L(l, l5, Length);
Copy_L(l, l6, Length);Copy_L(l, l7, Length);
Print(l);
BubbleSort(l, bubble_c, bubble_s);
InsertSort(l2, insert_c, insert_s);
SelectEasy(l3, easy_c, easy_s);
int d[]={40,30,20,10,5,3,1};
int t=7;
ShellSort(l4, d, t, shell_c, shell_s);
QuickSort(l5, quick_c, quick_s);
HeapSort(l6, heap_c, heap_s);
MergeSort(l7, merge_c, merge_s);
printf("\nSORT 关键字比较次数 关键字移动次数 \n");
printf("Bubble %-25d%-20d\n\n",bubble_c, bubble_s);
printf("Insert %-25d%-20d\n\n",insert_c, insert_s);
printf("Easy %-25d%-20d\n\n",easy_c, easy_s);
printf("Shell %-25d%-20d\n\n",shell_c, shell_s);
printf("Quick %-25d%-20d\n\n",quick_c, quick_s);
printf("Heap %-25d%-20d\n\n",heap_c, heap_s);
printf("Merge %-25d%-20d\n\n",merge_c, merge_s);
Print(l);
printf("The length of List:%d\n",Length);
bubble_c=0,bubble_s=0;
insert_c=0,insert_s=0;
easy_c=0,easy_s=0;
shell_c=0,shell_s=0;
quick_c=0,quick_s=0;
heap_c=0,heap_s=0;
merge_c=0,merge_s=0;
Destroy(l);Destroy(l2);Destroy(l3);Destroy(l4);Destroy(l5);Destroy(l6);Destroy(l7);
}while(select<=3 && select >=1);
return 0;
}