【比赛报告】牛客OI周赛1-提高组 NOIP练习赛卷六

比赛链接

A.分组

链接：https://www.nowcoder.com/acm/contest/199/A
来源：牛客网

---

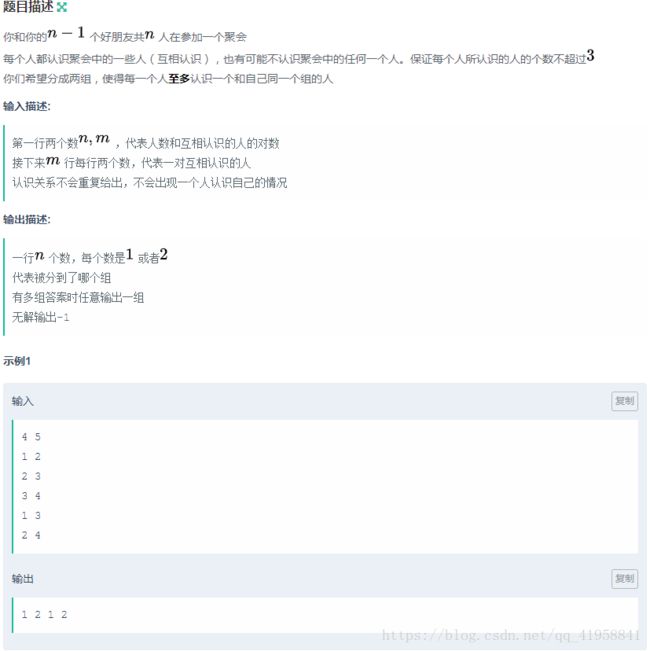
将认识关系转化为图中的边。dfs这张图，对每一个没有被访问过的点，将它标记为源点的反色，回溯的时候统计每个点有多少同色相邻点，个数等于2时将其颜色转换。

#include
#include
const int N=1e5+10,M=2e5+10;
int n,m,tot,vis[N],hd[N];
struct Edge{
	int v,nx;
}e[M<<1];
void dfs(int u)
{
	int cnt=0;
	for(int i=hd[u];~i;i=e[i].nx)
	    if(!vis[e[i].v])vis[e[i].v]=vis[u]^3,dfs(e[i].v);
	for(int i=hd[u];~i;i=e[i].nx)
	    cnt+=(vis[e[i].v]==vis[u]);
	if(cnt==2)vis[u]^=3;
}
void add(int u,int v)
{
	e[tot].v=v;
	e[tot].nx=hd[u];
	hd[u]=tot++;
}
int main()
{
	//freopen("in.txt","r",stdin);
	memset(hd,-1,sizeof(hd));
	scanf("%d%d",&n,&m);
    int u,v;
	for(int i=1;i<=m;i++)
    	scanf("%d%d",&u,&v),add(u,v),add(v,u);
    for(int i=1;i<=n;i++)
    	if(!vis[i])vis[i]=1,dfs(i);
    for(int i=1;i<=n;i++)
        printf("%d ",vis[i]);
    puts("");
    return 0;
}

总结

初看比赛结果发现这题只有1人满分，然后就被吓着了。在想会不会是并查集，或者在图中找环，后来发现这里的认识关系不会传递，且节点度数不超过3，肯定会存在一种解。

---

B.树

链接：https://www.nowcoder.com/acm/contest/199/B
来源：牛客网

---

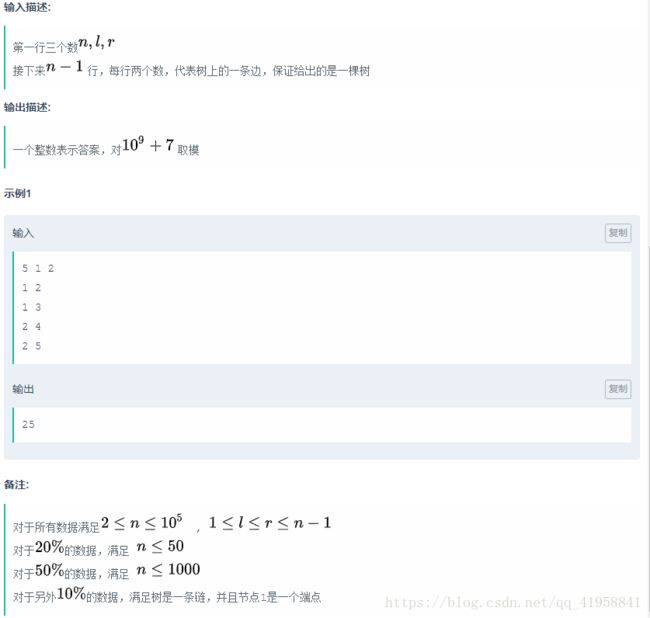
学习了大佬代码。对着这份代码看了一个多小时好像有点点明白。大概就是在这头选两个端点在那头选两个端点更新答案（说了等于没说）。选子树内那一头是不能在同一个子节点的子树内部选两个（会多占一些边），选子树外那头也得把共了边的部分减去，保证最后往上跳之后求出来的路径组合长度是在范围内的。

#include
#include
const int N=1e5+10,mod=1e9+7;
int hd[N],tot,n,sz[N],dep[N],fa[N][20],a[N],l,r,b[N],ans;
struct Edge{
	int v,nx;
}e[N<<1];
int C2(int x){return 1ll*x*(x-1)/2%mod;}//返回C(x,2) 
void add(int u,int v)
{
	e[tot].v=v;
	e[tot].nx=hd[u];
	hd[u]=tot++;
}
void dfs(int u)
{
	sz[u]=1;
	for(int i=1;(1<=0;i--)if(d&(1<

总结

看了个似懂非懂，但是时间非常有限，不能再继续看了。（我连样例答案都推不出来）

---

C.序列

链接：https://www.nowcoder.com/acm/contest/199/C
来源：牛客网

---

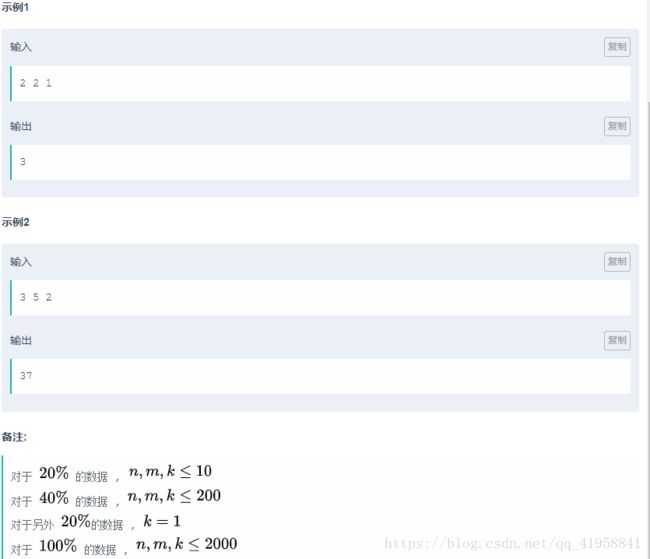
我们枚举不同数字的个数 $x$ 。此时等价于这个问题，有 $x$ 个箱子排成一排，任
意两个箱子之间距离不超过 $k$（超过 $k$ 意味着可以把这个间距减小到 $k$，且是一个等价的序
列），第一个箱子和最后一个箱子的距离不超过 $m$ 的方案数。设 $F[i,j]$ 表示放置了 $i$ 个箱子，第 $1$ 个箱子和最后一个箱子的距离为 $j$ 的方案数。
$$F[i,j]=\sum _{l=1}^{j-1}F[i-1,l]$$
注意要减去超过 $k$ 的那些方案数。观察到这个状态转移方程可以利用前缀和优化至 $O(n^2)$ 。
将 $n$ 个位置放入 $x$ 种不同数字一共有 $S[n,k]$ 种不同的方法，其中 $S$ 代表第二类斯特林数。
然后还要对 $x$ 个数字进行大小定位，共有 $x!$ 种不同方法。
目标：
$$\sum _{i=1}^n\sum _{j=0}^{m}S[n,i]\ast i!\ast f[i,j]$$

#include
#include
using namespace std;
typedef long long ll;
const ll mod=998244353;
const int N=2e3+10;
int n,m,k;
ll fac[N],sum[N],f[N][N],s[N][N],ans;
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    fac[0]=1;
    for(int i=1;i<=n;i++)
    {
    	s[i][1]=s[i][i]=1;fac[i]=(fac[i-1]*i)%mod;
    	for(int j=2;j

总结

初拿到这道题毫无头绪。这题转化为一个放箱子的模型，通过一系列分析利用DP求解，很巧妙。

---

比赛总结

这三题我几乎都没什么好的思路。T1难度其实并不高，但是思维走偏了。应该要充分发掘题目隐藏的性质。T2T3都是求方案数，自己在这方面比较薄弱。T2枚举端点那个地方不好懂，不过这种方法确实很好，利用倍增直接往上跳然后更新答案。T3的模型很好，把它转化为一个放箱子的问题然后就可以动态规划。而DP时通过观察状态转移方程发现 $i-1$ 阶段全都已经计算过，可以直接维护一个前缀和来优化时间复杂度。还有第二类斯特林数和阶乘来计算方案数，感觉确实很复杂。
出题人是个狼人。