2019 南京网络赛 E. K Sum(莫比乌斯反演 + 杜教筛)
化简 f n ( k ) = ∑ l 1 = 1 n ∑ l 2 = 1 n . . . ∑ l k = 1 n ( g c d ( l 1 , l 2 , . . . , l k ) ) 2 f_n(k)=\sum_{l_1 = 1}^n\sum_{l_2 = 1}^n...\sum_{l_k = 1}^n(gcd(l_1,l_2,...,l_k))^2 fn(k)=l1=1∑nl2=1∑n...lk=1∑n(gcd(l1,l2,...,lk))2 = ∑ d = 1 n ∑ l 1 = 1 n ∑ l 2 = 1 n . . . ∑ l k = 1 n d 2 ∗ [ g c d ( l 1 , l 2 , . . . , l k ) = d ] =\sum_{d = 1}^n\sum_{l_1 = 1}^n\sum_{l_2 = 1}^n...\sum_{l_k = 1}^nd^2*[gcd(l_1,l_2,...,l_k) = d] =d=1∑nl1=1∑nl2=1∑n...lk=1∑nd2∗[gcd(l1,l2,...,lk)=d] = ∑ d = 1 n ∑ l 1 = 1 ⌊ n d ⌋ ∑ l 2 = 1 ⌊ n d ⌋ . . . ∑ l k = 1 ⌊ n d ⌋ d 2 ∗ [ g c d ( l 1 , l 2 , . . . , l k ) = 1 ] =\sum_{d = 1}^n\sum_{l_1 = 1}^{\lfloor\frac{n}{d}\rfloor}\sum_{l_2 = 1}^{\lfloor\frac{n}{d}\rfloor}...\sum_{l_k = 1}^{\lfloor\frac{n}{d}\rfloor}d^2*[gcd(l_1,l_2,...,l_k) = 1] =d=1∑nl1=1∑⌊dn⌋l2=1∑⌊dn⌋...lk=1∑⌊dn⌋d2∗[gcd(l1,l2,...,lk)=1] = ∑ d = 1 n d 2 ∑ l 1 = 1 ⌊ n d ⌋ ∑ l 2 = 1 ⌊ n d ⌋ . . . ∑ l k = 1 ⌊ n d ⌋ ∑ p ∣ g c d ( l 1 , l 2 , . . . , l k ) μ ( p ) =\sum_{d = 1}^nd^2\sum_{l_1 = 1}^{\lfloor\frac{n}{d}\rfloor}\sum_{l_2 = 1}^{\lfloor\frac{n}{d}\rfloor}...\sum_{l_k = 1}^{\lfloor\frac{n}{d}\rfloor}\sum_{p |gcd(l_1,l_2,...,l_k)}\mu(p) =d=1∑nd2l1=1∑⌊dn⌋l2=1∑⌊dn⌋...lk=1∑⌊dn⌋p∣gcd(l1,l2,...,lk)∑μ(p) = ∑ d = 1 n d 2 ∑ p = 1 ⌊ n d ⌋ μ ( p ) ∑ l 1 = 1 ⌊ n p ∗ d ⌋ ∑ l 2 = 1 ⌊ n p ∗ d ⌋ . . . ∑ l k = 1 ⌊ n p ∗ d ⌋ =\sum_{d = 1}^nd^2\sum_{p = 1}^{\lfloor\frac{n}{d}\rfloor}\mu(p)\sum_{l_1 = 1}^{\lfloor\frac{n}{p * d}\rfloor}\sum_{l_2 = 1}^{\lfloor\frac{n}{p *d}\rfloor}...\sum_{l_k = 1}^{\lfloor\frac{n}{p * d}\rfloor} =d=1∑nd2p=1∑⌊dn⌋μ(p)l1=1∑⌊p∗dn⌋l2=1∑⌊p∗dn⌋...lk=1∑⌊p∗dn⌋ = ∑ T = 1 n ∑ d ∣ T d 2 ∗ μ ( T d ) ∗ ( ⌊ n T ⌋ ) k =\sum_{T = 1}^n\sum_{d|T}d^2 * \mu(\frac{T}{d})*(\lfloor\frac{n}{T}\rfloor)^k =T=1∑nd∣T∑d2∗μ(dT)∗(⌊Tn⌋)k
化简答案式子
∑ i = 2 k f n ( i ) = ∑ i = 2 k ∑ T = 1 n ∑ d ∣ T d 2 ∗ μ ( T d ) ∗ ( ⌊ n T ⌋ ) i \sum_{i = 2}^kf_n(i) = \sum_{i = 2}^k\sum_{T = 1}^n\sum_{d|T}d^2 * \mu(\frac{T}{d})*(\lfloor\frac{n}{T}\rfloor)^i i=2∑kfn(i)=i=2∑kT=1∑nd∣T∑d2∗μ(dT)∗(⌊Tn⌋)i = ∑ T = 1 n ∑ d ∣ T d 2 ∗ μ ( T d ) ∗ ∑ i = 2 k ( ⌊ n T ⌋ ) i =\sum_{T = 1}^n\sum_{d|T}d^2 * \mu(\frac{T}{d})*\sum_{i = 2}^k(\lfloor\frac{n}{T}\rfloor)^i =T=1∑nd∣T∑d2∗μ(dT)∗i=2∑k(⌊Tn⌋)i
后一项是等比数列求和,可用欧拉定理降幂,特判公比为1的情况。
令 g ( T ) = ∑ d ∣ T d 2 ∗ μ ( T d ) g(T) = \sum_{d|T}d^2 * \mu(\frac{T}{d}) g(T)=∑d∣Td2∗μ(dT),需要预处理 g g g的前缀和。
首先很明显 g ( T ) g(T) g(T)是一个积性函数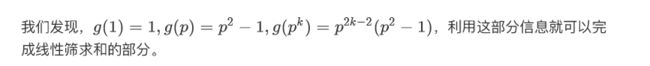
需要预处理大概 1 0 6 10^6 106的前缀和
(不会线性筛也可以用 n log n n\log n nlogn的暴力筛,比如我)
因为 g = μ ∗ I d 2 g = \mu*Id^2 g=μ∗Id2, g ∗ I = μ ∗ I ∗ I d 2 = I d 2 g * I = \mu * I * Id^2 =Id^2 g∗I=μ∗I∗Id2=Id2(狄力克雷卷积满足交换律,结合律)
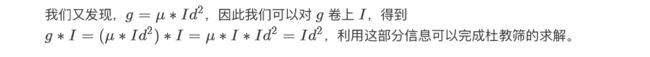
复杂度: O ( 1 0 6 log 1 0 6 + n 2 3 + n log ( 1 0 9 ) ) O(10^6\log 10^6 + n^{\frac{2}{3}} +\sqrt n \log (10^9)) O(106log106+n32+nlog(109)),第一项取决于筛的方法
代码:
#include