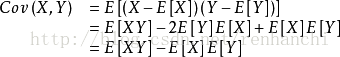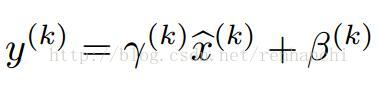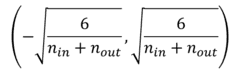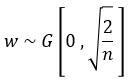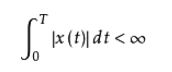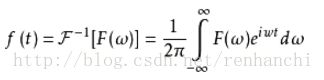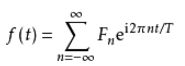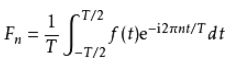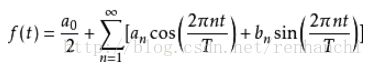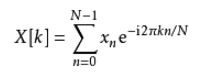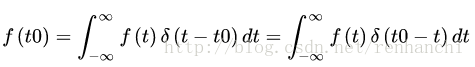【Machine Learning】【Math】常用定义备忘录(线性代数、概率论、统计学)
不断学习大量新知识,有些内容掌握的快,遗忘的也快。所以弄个备忘录,方便快速查看。
【2017.6.14 开始记录】--------------------------------------------------------------------------------------------------------------------------------------------------------------
期望(数学期望):
均值。 试验中每次可能结果的概率乘以其结果的总和。
标准差(均方差):
与均值差的平方和的平方根,用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据,标准差未必相同。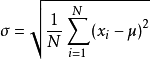
方差:
表示数据的离散程度,就是变量和期望的离散程度。标准差的平方。
协方差:
用于衡量两个变量的总体误差。 方差是协方差的一种特殊情况,即当两个变量是相同的情况。期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为:
L-1范数:
绝对值的和
L-2范数:
平方和的平方根
L-N范数:
N次方和的N方根
曼哈顿距离:
L-1距离
欧式距离(欧几里得度量):
L-2距离
交叉熵:
可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。 ![]() ,也可以写作: -Ep(xi)*log(q(xi))
,也可以写作: -Ep(xi)*log(q(xi))
【2017.6.23 更新】--------------------------------------------------------------------------------------------------------------------------------------------------------------
最小二乘(最小平方,OLS):
最小化误差平方和,寻求参数。拟合,回归。通过求偏导解参数,带入原函数得到数学模型。L-2距离
最大似然估计(MLE):
在已知试验结果(即是样本)的情况下,用来估计满足这些样本分布的参数,把可能性最大的那个参数θ作为真实θ*的参数估计。反推最大概率能达到已知结果的参数值。Kullback-Leibler距离(相对熵)。
Kullback-Leibler距离(相对熵):
DKL(P|Q)用于度量同一概率空间两个概率分布P,Q之间的距离,在实际应用中P往往代表的是数据真实的分布,而Q一般是对P的逼近.![]()
【2017.7.6 更新】--------------------------------------------------------------------------------------------------------------------------------------------------------------
径向基函数:
径向基函数是一个取值仅仅依赖于离原点距离的实值函数,也就是Φ(x)=Φ(‖x‖),或者还可以是到任意一点c的距离,c点称为中心点,也就是Φ(x,c)=Φ(‖x-c‖)。任意一个满足Φ(x)=Φ(‖x‖)特性的函数Φ都叫做径向基函数,标准的一般使用欧氏距离(也叫做欧式径向基函数),尽管其他距离函数也是可以的。在神经网络结构中,可以作为全连接层和ReLU层的主要函数。在支持向量机中,作为核函数。SVM中参数gamma就是径向基函数的参数。
【2017.7.27 更新】--------------------------------------------------------------------------------------------------------------------------------------------------------------
决定记一些ML的内容,平时工作只是使用框架工具。底层知识看了很多,还是会忘。
初始化:
让数据具有0均值和单位方差,减去均值,除以方差。
1. 卷积神经网络训练和测试的时候会将输入减去均值,目的是让输入分布在原点周围,加快拟合速度。
2. 输入数据初始化一般还有白化,就是去相关性。常用的方法有PCA白化:对数据PCA操作后,在进行方差归一化。白化计算量大,反向传播不一定可导,所以不推荐使用。
3. Batch Normalization:只是下面算法,随着层数加深会降低模型的表达能力。所以加了两个参数(图2)。
图1 图2
以上参考自:http://blog.csdn.net/elaine_bao/article/details/50890491
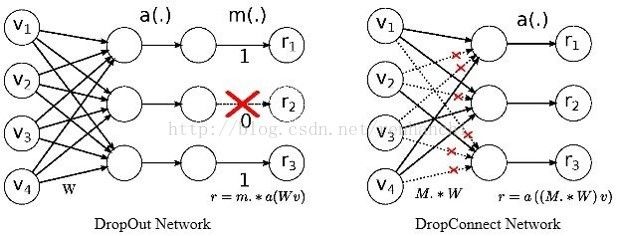
DropOut:
作用是防止过拟合。加深网络层数和增加神经元数量(deeper and wider)可以提高CNN的表达和分类能力,但会更容易过拟合。
这个方法可以使用在任意层之后。
具体点说,就是在训练的时候,随机让部分网络节点不工作,即输出为0。
DropConnect:
训练的时候,随机让部分权重为0。其他同上。
以上参考自: http://blog.csdn.net/elaine_bao/article/details/50890473
【2017.8.31 更新】--------------------------------------------------------------------------------------------------------------------------------------------------------------
卷积网络参数初始化
如果参数初始化太小,那么数据在每层传递时逐渐缩小而难以产生作用。如果初始化数值太大,那么数据在每层间传递时逐渐放大而导致发散和失效。
1. xavier初始化就是将参数在下面范围均匀分布。与ReLU搭配效果突出。in表示当前层输入维度,out表示当前层输出维度。
2. MSRAFiler初始化,只考虑输入个数时,初始化是一个0均值,2/n方差的高斯分布。
3. uniform初始化就是把参数进行均匀分布初始化,用min和max控制上下限,默认为(0,1)。
4. Gaussian初始化,根据给定的均值和标准差生成高斯分布。
5. constant初始化,根据给定常数初始化参数,默认为0。
【2017.11.14 更新】--------------------------------------------------------------------------------------------------------------------------------------------------------------
第一类间断点(discontinuity point of the first kind)
如果x0是函数f(x)的间断点,且左极限和右极限都存在,则称x0为函数f(x)的第一类间断点。
在第一类间断点中,左右极限相等且不等于f(x0)者称为可去间断点,不相等者称为跳跃间断点。
非第一类间断点即为第二类间断点(discontinuity point of the second kind)
狄里赫利条件(Dirichlet Conditions)
有的地方会写成“狄里赫莱条件”
狄里赫利认为,只有在满足一定条件时,周期信号才能展开成傅里叶级数。其内容为:
1.函数在任意有限区间内连续,或只有有限个第一类间断点。
2.在一个周期内,函数有有限个极大值或极小值。
3.x(t)在单个周期内绝对可积,即
傅里叶变换(Fourier Transform)
定义:f(t)是t的周期函数,如果t满足狄里赫利条件,则有下式成立。称为积分运算f(t)的傅里叶变换
下列公式的积分运算叫做F(ω)的傅里叶逆变换。
F(ω)叫做f(t)的 像函数,
f(t)叫做F(ω)的 像原函数。
F(ω)是f(t)的 像,
f(t)是F(ω)的 原像。
傅里叶级数(Fourier Series)
连续形式的傅里叶变换其实是傅里叶级数的推广,因为积分其实是一种极限形式的求和算子。
对于周期函数,它的傅里叶级数表示被定义为:
其中T为函数的周期,Fn为傅里叶展开系数:
对于实值函数(值域为实数的函数),函数的傅里叶级数可以写成:
其中,an和bn是实频率分量的振幅。
离散傅里叶变换(Discrete Fourier Transform,DFT)
为了在科学计算和数字信号处理等领域使用计算机进行傅里叶变换,必须将函数定义在离散点上而非连续域内,且须满足有限性或周期性条件。
这种情况下,序列![]() 的离散傅里叶变换为:
的离散傅里叶变换为:
其逆变换为:
直接使用DFT的定义计算的计算复杂度为O(N的平方),而快速傅里叶变换(Fast Fourier Transform,FFT)可以将复杂度改进为O(nlogn)。
以上内容参考自《百度百科》
更详细的傅里叶变换公式理解,可以参考:https://www.zhihu.com/question/19714540
含义、意义理解,可以参考:https://zhuanlan.zhihu.com/wille/19763358
复数运算
加法:实部相加,虚部相加。
减法:实部相减,虚部相减。
乘法:
(a,ib)×(c,id)
=ac + aid + ibc + i^2bd
=(ac - db)+ i(ad + bc)
(i^2 = -1)
如果放在坐标系中表示复数,则横轴为实数部分,纵轴为虚数部分。
复数(a,ib)的模长为 sqrt(a^2 + b^2)
同理可以得出复数的乘法运算在坐标系中体现为:模长相乘,幅角相加。
多项式的系数表示与点值表示
一个最高次项为n的多项式,有n+1个系数。(0 ~ n)
1.如果将这n+1个系数构成一个n+1维的向量,可以唯一的确定出一个多项式。这个向量就是系数表达式。
2.如果带入n个数字,求算出n个对应的值,可以唯一的确定出一个多项式,这些数字和值就构成了点值表达式。
克罗内克积(Kronecker Product)
A 圈乘B,如果A是一个m×n的矩阵,而B是一个p×q的矩阵,克罗内克积则是一个mp×nq的分块矩阵。
【2017.11.15 更新】--------------------------------------------------------------------------------------------------------------------------------------------------------------
狄拉克δ函数(Dirac Delta Function)
定义:
性质:
根据其性质,δ(t)可以用来表示任意一个信号。
并且在傅里叶变换公式推导中,有用到此性质。
未完待续…