Word2Vec 与《Distributed Representations of Words and Phrases and their Compositionality》学习笔记
什么是Word2Vec
目录
- 词嵌入 ( w o r d (word (word e m b e d d i n g ) embedding) embedding)
- 词嵌入的特点
- 嵌入矩阵
- S k i p − g r a m Skip-gram Skip−gram模型
- 分层 S o f t m a x Softmax Softmax ( H i e r a r c h i c a l (Hierarchical (Hierarchical S o f t m a x ) Softmax) Softmax)
- 负采样
- 其他细节
词嵌入 ( w o r d (word (word e m b e d d i n g ) embedding) embedding)
简单来说, e m b e d d i n g embedding embedding就是用一个低维的向量表示一个词。在词向量提出之前,人们经常采用 o n e one one h o t hot hot e n c o d i n g encoding encoding对词语进行编码。但由于 o n e one one h o t hot hot e n c o d i n g encoding encoding的维度等于词语的总数,比如阿里的商品 o n e one one h o t hot hot e n c o d i n g encoding encoding的维度就至少是千万量级的。这样的编码方式对于商品来说是极端稀疏的,而深度学习的特点以及工程方面的原因使其不利于稀疏特征向量的处理,因此,如果能把物体编码为一个低维稠密向量再喂给神经网络,自然是一个高效的基本操作,词嵌入应运而生。
词嵌入的特点
词向量中的值并不是随意给出的而是经过训练得到的,是可以表示一定特征的,所以两个词向量之间的距离可以表示两个词相似的程度;词向量还可以进行类比操作。比如已知 m a n man man类比于 w o m a n woman woman,问 k i n g king king类比于什么,显然我们知道是 q u e e n ( 王 后 ) queen(王后) queen(王后),如果用词向量, m a n man man与 w o m a n woman woman是向量空间的两个点,两者连成一个向量应该和 k i n g king king这个点与未知点所连向量是相等向量(或者相差很小),我们可以遍历一下,便最终可以得到 q u e e n queen queen这个点。这就是词向量的类比操作。

如上图所示,我们假设上面的六个单词经过词嵌入得到了4维向量,词向量每一个维度都可以表现出一定的具体意义,在上图中分别是性别,王室信息,年龄和食物属性。我们对男人女人两个向量做差得到的向量和皇帝与皇后两个向量做差得到向量,相差很小,这就是一种类比关系。

在向量空间中两个向量是平行的。
嵌入矩阵
那么用什么来表示词向量呢?答案是嵌入矩阵。
我们假设在字典中有 10000 10000 10000个单词,每一个单词都有一个 o n e one one h o t hot hot v e c t o r vector vector与之对应,这样就有 10000 10000 10000个向量与字典中的单词构成一一映射。我们假设我们要经过词嵌入,将这些 o n e one one h o t hot hot v e c t o r vector vector转化成 300 300 300维词向量,那么我们就定义一个 10000 ∗ 300 10000 * 300 10000∗300的嵌入矩阵W:
e = x W e =xW e=xW
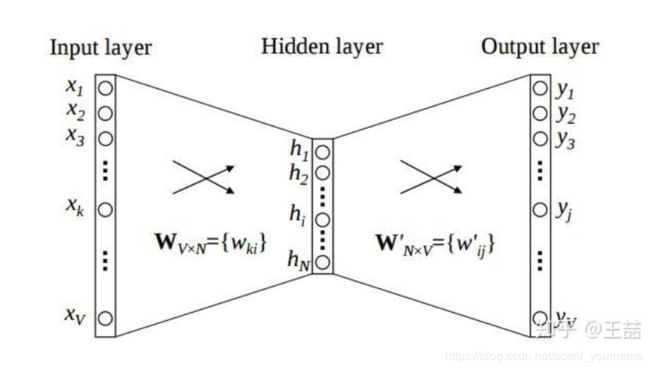
上图神经网络模型中 I n p u t Input Input l a y e r layer layer代表的是 o n e one one h o t hot hot v e c t o r vector vector而隐藏层 ( H i d d e n (Hidden (Hidden l a y e r ) layer) layer)则代表词向量, W V ∗ N W_{V*N} WV∗N则是嵌入矩阵,所以获得词向量的过程就是通过一个神经网络定义损失函数,训练嵌入矩阵的过程。
S k i p − g r a m Skip-gram Skip−gram模型
- S k i p − g r a m Skip-gram Skip−gram是一种获得词嵌入的模型,也是 W o r d 2 V e c Word2Vec Word2Vec最基础的方法之一。
- 我们假定训练样本是一个句子,这个句子由 T T T个词构成 w 1 w 2 . . . . . . w T w_{1}w_{2}......w_{T} w1w2......wT,每个词都跟其相邻的词的关系最密切,换句话说每个词都是由相邻的词决定的 ( C B O W (CBOW (CBOW模型的动机 ) ) ),或者每个词都决定了相邻的词 ( S k i p − g r a m (Skip-gram (Skip−gram模型的动机 ) ) )。如下图所示,输入一个词周边的几个词,预测这个词的模型是 C B O W CBOW CBOW模型,而输入是这个词本身,预测这个词周围的词的模型则是 S k i p − g r a m Skip-gram Skip−gram模型。
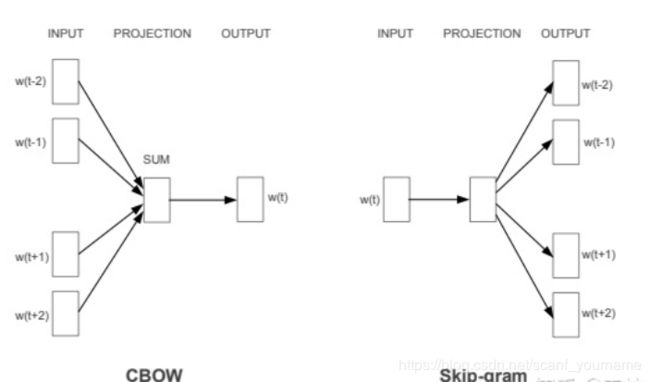
举个例子,现在有一个句子: I I I w a n t want want a a a g l a s s glass glass o f of of j u i c e juice juice t o to to g o go go a l o n g along along w i t h with with m y my my c e r e a l . cereal. cereal.如果输入是 a a a g l a s s glass glass o f of of ∗ ∗ ∗ ∗ ∗ ***** ∗∗∗∗∗ t o to to g o go go a l o n g , along, along, 出是 j u i c e juice juice则是 C B O W CBOW CBOW模型;如果输入是 j u i c e , juice, juice,输出是 a a a g l a s s glass glass o f of of和 t o to to g o go go a l o n g along along ,则是 S k i p − g r a m Skip-gram Skip−gram模型。我们主要介绍的是 S k i p − g r a m Skip-gram Skip−gram模型。 - 那么为了产生模型的正样本,我们选一个长度为 2 c + 1 2c+1 2c+1(目标词前后各选 c c c个词)的滑动窗口,从句子左边滑倒右边,每滑一次,窗口中的词就形成了我们的一个正样本。
- 有了训练样本之后我们就可以着手定义优化目标了,既然每个词 w t w_{t} wt都决定了相邻词 w t + j w_{t+j} wt+j基于极大似然,我们希望所有样本的条件概率 P ( w t + j ∣ w t ) P(w_{t+j}|w_{t}) P(wt+j∣wt)之积最大,这里我们使用log probability。我们的目标函数有了:

接下来的问题是怎么定义 P ( w t + j ∣ w t ) P(w_{t+j}|w_{t}) P(wt+j∣wt) ,作为一个多分类问题,最简单最直接的方法当然是直接用 S o f t m a x Softmax Softmax函数,公式如下图所示:

其中 W W W代表的是字典的大小, v w i v_{wi} vwi和 v w ′ v_{w}^{'} vw′是由一个神经网络产生的,如下图所示:
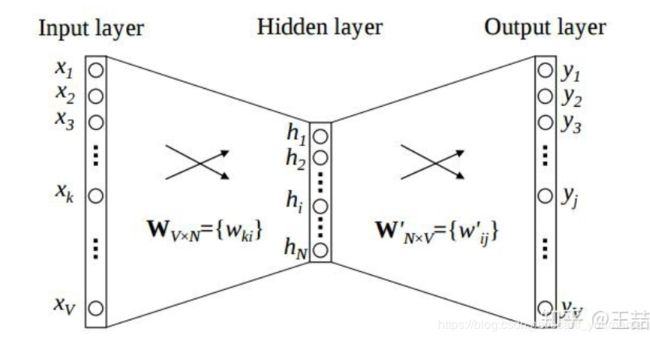
这个图在刚才介绍嵌入矩阵的时候向大家展示过,其中 v w i v_{wi} vwi代表的是隐藏层的向量 h = ( h 1 h 2 . . . . h N ) h=(h_{1}h_{2}....h_{N}) h=(h1h2....hN)而 v w ′ v_{w}^{'} vw′代表的是系数矩阵 W N ∗ V ′ W_{N*V}^{'} WN∗V′的一列参数(第w列),那么隐藏层向量 h h h与系数矩阵 W N ∗ V ′ W_{N*V}^{'} WN∗V′做向量乘法得到的是什么呢?很简单,就是输出层向量 y = y 1 y 2 . . . . y V y=y_{1}y_{2}....y_{V} y=y1y2....yV,所以上面的 S o f t m a x Softmax Softmax公式的意思就是对于输出层向量 y y y再经过一个 S o f t m a x Softmax Softmax层得到的就是每一个词对应的概率。用正样本定义的损失函数来反向传播,使定义的公式的值尽可能大,从而训练了嵌入矩阵。 - 以上就是最基本的 S k i p − g r a m Skip-gram Skip−gram模型,这个模型的缺点就是在字典大小特别大的时候,训练难度会急剧增加,因为根据定义 S o f t m a x Softmax Softmax需要依次计算所有单词与特定单词之间的内积,这样计算量会非常大,不利于训练大规模数据模型。
分层 S o f t m a x Softmax Softmax ( H i e r a r c h i c a l S o f t m a x ) (Hierarchical Softmax) (HierarchicalSoftmax)
- 分层 S o f t m a x Softmax Softmax ( H i e r a r c h i c a l S o f t m a x ) (Hierarchical Softmax) (HierarchicalSoftmax)是对于之前 S o f t m a x Softmax Softmax的一种优化,用于解决在大规模数据上难以训练的问题。
- 分层 S o f t m a x Softmax Softmax使用二叉树表示输出层,其中 W W W个单词作为其叶子节点,并且对于每个内部节点,显式地表示其子节点的相对概率。举个例子: I I I w a n t want want a a a g l a s s glass glass o f of of j u i c e juice juice t o to to g o go go a l o n g along along w i t h with with m y my my c e r e a l . cereal. cereal. 我们现在想要知道 p ( g l a s s ∣ o r a n g e ) p(glass|orange) p(glass∣orange),根据建立的二叉树,我们已知走到叶子节点 g l a s s glass glass的路径,现在我们从根节点出发,根据每一个内部节点为glass分配的概率,一步步的走到 g l a s s glass glass对应的叶子节点,我们将所有的概率相乘就得到了 p ( g l a s s ∣ o r a n g e ) p(glass|orange) p(glass∣orange)。具体公式如下:

L ( w ) L(w) L(w)代表的是w对应的叶子节点是深度,设 n ( w , j ) n(w,j) n(w,j)为从root到单词 w w w的路径上的第 j j j个节点,则 n ( w , 1 ) = r o o t , n ( w , L ( w ) ) = w 。 n(w,1)=root,n(w,L(w))=w。 n(w,1)=root,n(w,L(w))=w。 [ [ x ] ] = 1 [[x]]=1 [[x]]=1 i f if if x = l e f t x=left x=left o t h e r w i s e − 1 otherwise−1 otherwise−1 - 分层 s o f t m a x softmax softmax使用的树结构对性能有相当大的影响。 M n i h Mnih Mnih和 H i n t o n Hinton Hinton探索了构建树结构的一些方法以及训练时间和结果模型精度的影响。在我们的工作中,我们使用一个霍夫曼树 ( b i n a r y (binary (binary H u f f m a n Huffman Huffman t r e e ) tree) tree),因为它将短codes分配给高频词,从而加快了训练速度。之前已经观察到,根据出现频率组合单词可以很好的作为基于神经网络的语言模型的一种简单加速技术。
负采样
- 我们上文书说到 S k i p − G r a m Skip-Gram Skip−Gram的缺点是在用 S o f t m a x Softmax Softmax计算时效率会很低,负采样时一种改善过的学习算法,可以解决这一问题,让我们去看看吧。
- 负采样的具体步骤如下:
- 算法思想:在负采样中我们做的不再是 S o f t m a x Softmax Softmax而是一个二分类问题。给定两个词,其中一个词做 C o n t e n t Content Content判断另一个词是不是 t a r g e t target target,如果是则输出1,如果不是则输出0。
- 首要任务还是如何构造训练集,训练集同样取自文本,先找到一组正取样,再选取n组负取样,将这n+1组数据作为输入训练神经网络,如下图所示:

第一行从文本中选取了一个正取样, C o n t e n t Content Content是 o r a n g e orange orange这个单词, T a r g e t Target Target是 j u i c e juice juice这个单词。对于 o r a n g e orange orange我们同时需要取 n n n个负取样,分别是后面的四组并标记为 0 0 0,在负取样中 T a r g e t Target Target是从字典中随机选取的。
此外还需要注意 n n n的选取,在论文中指出,如果在小数据集上 n n n选取 5 − 20 5-20 5−20比较好,如果数据集规模变大, n n n的取值随之减小,在大数据集上 n n n取 2 − 5 2-5 2−5。 - 下面我们看看如何建立这个监督学习的模型( l o g i s t i c logistic logistic回归模型),首先定义输出:
P ( y = 1 ∣ c , t ) = σ ( θ t T e c ) P(y=1|c,t)=\sigma (\theta _{t}^{T}e_{c}) P(y=1∣c,t)=σ(θtTec)
和之前 S o f t m a x Softmax Softmax一样 θ t \theta _{t} θt是一个属于 T a r g e t Target Target的参数需要训练, e c e_{c} ec是词向量来自嵌入矩阵。 - 最后看一下模型,如下图:
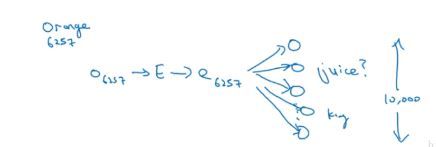
前面的过程和前一节是一样的,我们主要关注的是最后一步,词向量和字典中的每一个词都会进行一次二分类,来判断这个词是否是 C o n t e n t Content Content的 T a r g e t Target Target。这样做的好处就是将一个 V a l u e S i z e ValueSize ValueSize的多分类转化成了 V a l u e S i z e ValueSize ValueSize个二分类问题,大大减少了计算提高了效率。此外我们每次迭代只需要更新 k k k个负样本和 1 1 1个正样本涉及到的单元也就是 k + 1 k+1 k+1个单元。
- 如何选取负样本?
- 根据文本中单词的词频取样,缺点是导致一些经常出现的词(比如:冠词、代词等)出现在负取样中偏多,导致模型经常做无谓的训练。
- 采用均匀分布的随机取样,缺点是没有代表性。
- 这是论文中提到的一个效果不错的取样方法(基于实践的经验吧),有如下公式:
P ( ω i ) = f ( ω i ) 3 / 4 ∑ j = 1 n f ( ω j ) 3 / 4 P(\omega _{i})=\frac{f(\omega _{i})^{3/4}}{\sum _{j=1}^{n}f(\omega _{j})^{3/4}} P(ωi)=∑j=1nf(ωj)3/4f(ωi)3/4
既然单纯用词频会导致某些我们不希望出现的词出现很多次,均匀分布又不具代表性,那么何不采取一种折中的办法,这个办法就是加权,用某个词词频的 3 / 4 3/4 3/4次方比上所有词词频的 3 / 4 3/4 3/4次方作为该词出现的频率。这个方法在实际应用中合情合理,效果不错。
其他细节
学习短语
- 对于某些词语,经常出现在一起的,我们就判定他们是短语。那么如何衡量呢?用以下公式:

输入两个词向量,如果算出的score大于某个阈值时,我们就认定他们是“在一起的”。
为了考虑到更长的短语,我们拿2-4个词语作为训练数据,依次降低阈值。
代码以及注释
'''
code by Tae Hwan Jung(Jeff Jung) @graykode
'''
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import matplotlib.pyplot as plt
#定义一个多维张量torch
dtype = torch.FloatTensor
# 3 Words Sentence
sentences = [ "i like dog", "i like cat", "i like animal",
"dog cat animal", "apple cat dog like", "dog fish milk like",
"dog cat eyes like", "i like apple", "apple i hate",
"apple i movie book music like", "cat dog hate", "cat dog like"]
#.join的用法是将元素以指定字符连接生成新的字符串,用split进行分割
word_sequence = " ".join(sentences).split()
word_list = " ".join(sentences).split()
#利用set的性质将重复的元素消去,之后再重新转化成list
word_list = list(set(word_list))
#enumerate是一个枚举的关键词,i是键,w是值,这样就将所有单词按照自然数编成字典
word_dict = {w: i for i, w in enumerate(word_list)}
# Word2Vec Parameter
batch_size = 20 # batch size 一批训练20组sample
embedding_size = 2 # 词嵌入的维数
voc_size = len(word_list) #字典的大小
def random_batch(data, size):
random_inputs = []
random_labels = []
#随机选取sample
random_index = np.random.choice(range(len(data)), size, replace=False)
for i in random_index:
#构建输入对应的one hot-vec
random_inputs.append(np.eye(voc_size)[data[i][0]]) # target
random_labels.append(data[i][1]) # context word
return random_inputs, random_labels
# Make skip gram of one size window
#构建输入的samples
skip_grams = []
for i in range(1, len(word_sequence) - 1):
target = word_dict[word_sequence[i]]
context = [word_dict[word_sequence[i - 1]], word_dict[word_sequence[i + 1]]]
for w in context:
skip_grams.append([target, w])
# Model
class Word2Vec(nn.Module):
#模型初始化,固定格式记住
def __init__(self):
super(Word2Vec, self).__init__()
# W and WT is not Traspose relationship
#初始化从输入到隐藏层的嵌入矩阵,参数随机初始化在(-1,1]
self.W = nn.Parameter(-2 * torch.rand(voc_size, embedding_size) + 1).type(dtype) # voc_size > embedding_size Weight
#随机初始化从隐藏层到输出层的系数矩阵,参数随机初始化在(-1,1]
self.WT = nn.Parameter(-2 * torch.rand(embedding_size, voc_size) + 1).type(dtype) # embedding_size > voc_size Weight
#定义前向传播,记得self也要作为参数传入
def forward(self, X):
# X : [batch_size, voc_size]
hidden_layer = torch.matmul(X, self.W) # hidden_layer : [batch_size, embedding_size]
output_layer = torch.matmul(hidden_layer, self.WT) # output_layer : [batch_size, voc_size]
return output_layer
model = Word2Vec()
#定义损失函数和优化
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
# Training
for epoch in range(5000):
input_batch, target_batch = random_batch(skip_grams, batch_size)
#被定义为Varialbe类型的变量可以认为是一种常量,在pytorch反向传播过程中不对其求导
input_batch = Variable(torch.Tensor(input_batch))
target_batch = Variable(torch.LongTensor(target_batch))
optimizer.zero_grad()
output = model(input_batch)
# output : [batch_size, voc_size], target_batch : [batch_size] (LongTensor, not one-hot)
loss = criterion(output, target_batch)
if (epoch + 1)%1000 == 0:
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.6f}'.format(loss))
loss.backward()
optimizer.step()
for i, label in enumerate(word_list):
W, WT = model.parameters()
x,y = float(W[i][0]), float(W[i][1])
plt.scatter(x, y)
plt.annotate(label, xy=(x, y), xytext=(5, 2), textcoords='offset points', ha='right', va='bottom')
plt.show()