【人脸识别】根据关键点进行人脸姿态估计

欧拉角（Euler Angle）

pitch：俯仰角，围绕X轴旋转;

yaw：偏航角，围绕Y轴旋转;

roll：翻滚角，围绕Z轴旋转。

第一步：用Opencv的solvePnP函数解出旋转向量

C++: 
bool solvePnP(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int flags=SOLVEPNP_ITERATIVE )
Python: 
cv2.solvePnP(objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, flags]]]]) → retval, rvec, tvec

• 输入
  objectPoints - 世界坐标系下的控制点的坐标，单位mm，vector的数据类型在这里可以使用;
  imagePoints - 在图像坐标系下对应的控制点的坐标，vector在这里可以使用;
  cameraMatrix - 相机的内参矩阵;
  
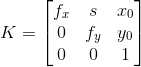
  distCoeffs - 相机的畸变系数;
  flags - 默认使用CV_ITERATIV迭代法，还有SOLVEPNP _P3P、SOLVEPNP _EPNP、SOLVEPNP _DLS、SOLVEPNP _UPNP;
  useExtrinsicGuess - 默认False，表示是否有初始化已知的旋转向量和平移向量;
  （其中相机内参矩阵与畸变系数可由张正友相机标定法得到）

• 输出
  rvec - 输出的旋转向量，使坐标点从世界坐标系旋转到相机坐标系;
  tvec - 输出的平移向量，使坐标点从世界坐标系平移到相机坐标系;

其中3D model，站坑以后看，得到3D点
https://github.com/YadiraF/PRNet

         LEFT_EYEBROW_LEFT = [6.825897, 6.760612, 4.402142]
         LEFT_EYEBROW_RIGHT = [1.330353, 7.122144, 6.903745]
         RIGHT_EYEBROW_LEFT = [-1.330353, 7.122144, 6.903745]
         RIGHT_EYEBROW_RIGHT = [-6.825897, 6.760612, 4.402142]
         LEFT_EYE_LEFT = [5.311432, 5.485328, 3.987654]
         LEFT_EYE_RIGHT = [1.789930, 5.393625, 4.413414]
         RIGHT_EYE_LEFT = [-1.789930, 5.393625, 4.413414]
         RIGHT_EYE_RIGHT = [-5.311432, 5.485328, 3.987654]
         NOSE_LEFT = [2.005628, 1.409845, 6.165652]
         NOSE_RIGHT = [-2.005628, 1.409845, 6.165652]
         MOUTH_LEFT = [2.774015, -2.080775, 5.048531]
         MOUTH_RIGHT = [-2.774015, -2.080775, 5.048531]
         LOWER_LIP = [0.000000, -3.116408, 6.097667]
         CHIN = [0.000000, -7.415691, 4.070434]
         landmarks_3D = np.float32([LEFT_EYEBROW_LEFT,
                                    LEFT_EYEBROW_RIGHT,
                                    RIGHT_EYEBROW_LEFT,
                                    RIGHT_EYEBROW_RIGHT,
                                    LEFT_EYE_LEFT,
                                    LEFT_EYE_RIGHT,
                                    RIGHT_EYEBROW_LEFT,
                                    RIGHT_EYEBROW_RIGHT,
                                    NOSE_LEFT,
                                    NOSE_RIGHT,
                                    MOUTH_LEFT,
                                    MOUTH_RIGHT,
                                    LOWER_LIP,
                                    CHIN])

第二步：旋转向量 ->旋转矩阵->欧拉角

1. 旋转矩阵->旋转向量

C++: 
void Rodrigues(InputArray src, OutputArray dst, OutputArray jacobian=noArray())
Python: 
cv2.Rodrigues(src[, dst[, jacobian]]) → dst, jacobian

src – 输入，旋转向量(3x1 or 1x3) or 旋转矩阵 (3x3);
dst – 输出，旋转矩阵(3x3) or 旋转向量 (3x1 or 1x3);
jacobian – 可选项，输出雅克比矩阵（39或者93），输入数组对输出数组的偏导数;

利用solvePnP得到的旋转向量，由Rodrigues可得到旋转矩阵，下面可由旋转矩阵求出欧拉角。

2. 判断是否为旋转矩阵

def isRotationMatrix(R):
    Rt = np.transpose(R)   #旋转矩阵R的转置
    shouldBeIdentity = np.dot(Rt, R)   #R的转置矩阵乘以R
    I = np.identity(3, dtype=R.dtype)           # 3阶单位矩阵
    n = np.linalg.norm(I - shouldBeIdentity)   #np.linalg.norm默认求二范数
    return n < 1e-6                            # 目的是判断矩阵R是否正交矩阵（旋转矩阵按道理须为正交矩阵，如此其返回值理论为0）

旋转矩阵为正交矩阵，根据正交矩阵的特性进行判断R*RT=E。

3. 旋转矩阵->欧拉角

def rotationMatrixToAngles(R):
    assert (isRotationMatrix(R))   #判断是否是旋转矩阵（用到正交矩阵特性）
    sy = math.sqrt(R[0, 0] * R[0, 0] + R[1, 0] * R[1, 0])  #矩阵元素下标都从0开始（对应公式中是sqrt(r11*r11+r21*r21)），sy=sqrt(cosβ*cosβ)
    singular = sy < 1e-6   # 判断β是否为正负90°
 
    if not singular:   #β不是正负90°
        x = math.atan2(R[2, 1], R[2, 2])
        y = math.atan2(-R[2, 0], sy)
        z = math.atan2(R[1, 0], R[0, 0])
    else:              #β是正负90°
        x = math.atan2(-R[1, 2], R[1, 1])
        y = math.atan2(-R[2, 0], sy)   #当z=0时，此公式也OK，上面图片中的公式也是OK的
        z = 0
    
    x = x*180.0/3.141592653589793
    y = y*180.0/3.141592653589793
    z = z*180.0/3.141592653589793
 
    return np.array([x, y, z])

参考：
https://docs.opencv.org/3.0-beta/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html#solvepnp
https://www.zhihu.com/question/47736315/answer/236284413