房价预测--利用Python进行数据分析

原文链接：https://www.kaggle.com/pmarcelino/comprehensive-data-exploration-with-python/notebook

在这篇文章中，我对原文的结论翻译并加入自己的一些理解，如有不当之处，请在评论提出建议和意见，谢谢~

在这个Kernel中，我们将针对房价预测问题，利用Python对这组数据进行全面而非详尽地分析。

本文的主要任务：

• 理解问题：研究并分析每个变量对于该问题的意义和重要性；
• 单变量研究：只关注于因变量“SalePrice”，并尝试了解关于它更多信息；
• 多变量研究：尝试理解因变量与自变量之间的关系；
• 清洗数据：清洗数据并处理缺失值、异常值并分类数据；
• 测试假设：检测数据是否满足要求。

准备工作

in[1]

#调用库
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
import warnings                   
warnings.filterwarnings('ignore')  #利用warnings模块来忽略匹配的警告
%matplotlib inline  #魔术命令“%”，当输入plt.plot()后，不必再输入 plt.show()，图像将自动显示出来

in[2]

#导入训练集
df_train = pd.read_csv('C:/Users/dell/Desktop/input/train.csv')

in[3]

#查看列名
df_train.columns

out[3]

Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street',
       'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig',
       'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType',
       'HouseStyle', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
       'RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType',
       'MasVnrArea', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual',
       'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1',
       'BsmtFinType2', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating',
       'HeatingQC', 'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF',
       'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
       'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual',
       'TotRmsAbvGrd', 'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType',
       'GarageYrBlt', 'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual',
       'GarageCond', 'PavedDrive', 'WoodDeckSF', 'OpenPorchSF',
       'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'PoolQC',
       'Fence', 'MiscFeature', 'MiscVal', 'MoSold', 'YrSold', 'SaleType',
       'SaleCondition', 'SalePrice'],
      dtype='object')

一、理解问题-认识数据

为了更清晰地认识数据，我们可以查看变量，并试图解读它的意义以及与该问题的相关性。虽然费事，但很有必要。本文提供了认识数据的一种思路，能够使我们的分析更有条理性。
我们可以创建一个包含以下列的Excel表格：

• Variable - 变量名称.；
• Type - 变量类型的标识。可定义两个：‘numerical’指值为数字的变量、‘categorical’指值为类别的变量；
• Segment - 变量段的标识。可定义三个：‘building’指与一个建筑的物理特性有关的变量，例如“OverallQual”、‘space’指关于房屋控件属性的变量，例如“TotalBsmtSF”、‘location’指房屋所在地信息的变量，例如“Neighborhood”；
• Expectation - 变量对于“SalePrice”的影响的期望。可设定‘High’、‘Medium’、‘Low’作为分类标尺；
• Conclusion - 在快速浏览数据后，我们对变量重要性的结论。可与‘Expectation’使用相同分类标尺；
• Comments - 我们对该变量任何一般性意见。

虽然‘Type’和‘Segment’只是未来可能的参考，但是‘Expectation’很重要。在填写这一栏时，我们应该在阅读所有变量描述后，逐一地问自己：

• 我们买房时会考虑该因素吗？（例如，我们是否在意‘砖石贴面类型？’）
• 如果考虑该因素，那么它有多重要呢？（例如，在外部使用优质材料而不是劣质材料时会有什么影响？）
• 该因素是否与其他因素重复了呢？（例如，“LandContour”给出了房产的平整度，那么还需要知道“LandSlope”吗？）

在经过这一系列分析后，我们可以筛选表格并关注于具有高期望值的变量（High Expenctation）。并通过画出这些变量与“SalePrice”的散点图，填入“Conclusion”栏，它是对我们预期的一个修正。

由此，我得出以下结论：
在该问题中，下列变量和该问题相关并且很重要：

• OverallQual 整体材料和表面质量
• YearBuilt 原始施工日期
• TotalBsmtSF 地下室总面积
• GrLivArea 居住面积

其中，“OverallQual”和“YearBuilt”是两个‘building’变量，而“TotalBsmtSF”和“GrLivArea”是两个‘space’变量。而这似乎违背了房地产商对于房屋位置的关注程度。这种快速检查数据的方式有点苛刻，例如，我们预期“NigBuffID”更相关，但在检查数据后排除了它。这也可能与我们数据可视化呈现的方式是有关系的，这里我们使用的是散点图而不是箱线图，散点图更适合于分类变量可视化。可视化数据的方式通常能够影响我们的结论。

但这次的分析主要目的是对我们的数据和预期结果有更多建设性的思考。上述的分析也已经达到了我们的目的。

二、单变量研究-分析“SalePrice”

首先，利用pandas的describe()函数给出“SalePrice”数据部分统计量。
in[4]:

df_train['SalePrice'].describe()

out[4]:

count      1460.000000   #非空值个数
mean     180921.195890   #均值
std       79442.502883   #样本标准差
min       34900.000000   #最小值
25%      129975.000000   #四分位点
50%      163000.000000   #中位数
75%      214000.000000   #四分位点
max      755000.000000   #最大值
Name: SalePrice, dtype: float64

我们再来看下“SalePrice”的分布情况。
in[5]:

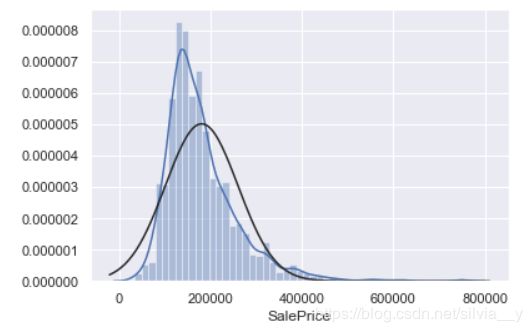
sns.distplot(df_train['SalePrice']); #数据分布直方图

out[5]:

我们可以看到，数据偏离整体分布，并且存在峰值。再来看下偏值与峰值的具体数据：
in[6]:

print("Skewness: %f" % df_train['SalePrice'].skew())   #skew()样本偏度值
print("Kurtosis: %f" % df_train['SalePrice'].kurt())   #kurt()样本峰度值

回顾：print()字符串格式化输出： “字符 %格式1 %格式2 字符”%(变量1,变量2)，%格式表示接受变量的类型。%s表示字符串，%f表示浮点数。
out[6]:

Skewness: 1.882876
Kurtosis: 6.536282

除此以外，我们还想看看“SalePrice”与其他变量之间的关系。在第一节中，我们分析出了四个较为重要的因素，其中两个‘space’变量“TotalBsmtSF”和“GrLivArea”，两个‘building’变量“OverallQual”和“YearBuilt”。在本节中，我们分别对这四个变量进行定量分析。
1、GrLivArea的数值分析
in[7]:

var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000)); #scatter()绘制散点图，ylim限制y轴坐标范围

回顾：pandas中的concat([a,b,c],axis=0/1)将a、b、c沿轴向连接，默认axis=0沿行，数据被拼接成一串；axiss=1沿列，数据并列拼接。
out[7]:

从图上我们能看出来，“GrLivArea”与“SalePrice”似乎线性正相关。再来看看“TotalBsmtSF”吧。
2、TotalBsmtSF的数值分析
in[8]:

var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

out[8]:

3、OverallQual的分类分析
in[9]：

var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6)) #plt.subplots()创建一个新的图片f，并返回包含了已生成子图对象的Numpy数组ax
fig = sns.boxplot(x=var, y="SalePrice", data=data)  #data为要输入的数据集
fig.axis(ymin=0, ymax=800000);

boxplot的详细用法参考：https://www.sohu.com/a/163963464_718302
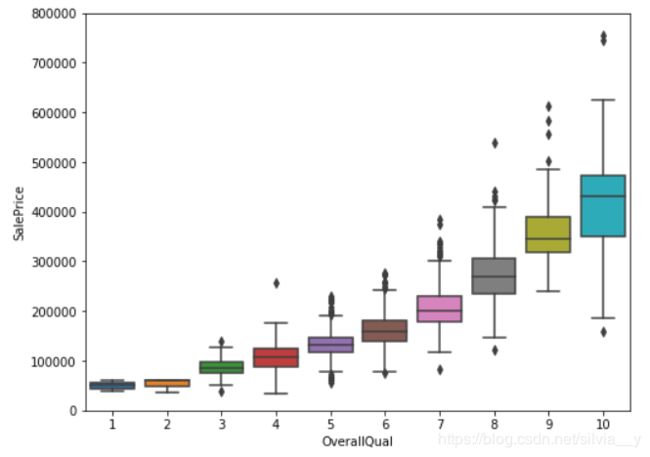
out[9]:

注：箱型图分析
箱形图可以用来观察数据整体的分布情况，利用中位数，25/%分位数，75/%分位数，上边界，下边界等统计量来来描述数据的整体分布情况。通过计算这些统计量，生成一个箱体图，箱体包含了大部分的正常数据，而在箱体上边界和下边界之外的，就是异常数据。
其中上下边界的计算公式如下：
UpperLimit=Q3+1.5IQR=75%分位数+（75%分位数-25%分位数）*1.5，
LowerLimit=Q1－1.5IQR=25%分位数-（75%分位数-25%分位数）*1.5
（将数据由小到大排序，处于中间的为中位数，即50%分位数，在75%位置的即为75%分位数或四分之三分位数——Q3，在25%位置的即为25%分位数或四分之一分位数——Q1）
参数说明：
1. Q1表示下四分位数，即25%分位数；Q3为上四分位数，即75%分位数；IQR表示上下四分位差，系数1.5是一种经过大量分析和经验积累起来的标准，一般情况下不做调整。
2. 分位数的参数可根据具体预警结果调整：25%和75%，是比较灵敏的条件，在这种条件下，多达25%的数据可以变得任意远而不会很大地扰动四分位。具体业务中可结合拟合结果自行调整为其他分位。

4、YearBuilt的分类分析
in[10]:

var = 'YearBuilt'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);  #x轴刻度旋转90度

out[10]:
虽然没有像“OverallQual”那么明显的趋势，但是大致上还是呈正相关性的。

综上所述：

• ‘GrLivArea’ 和 ‘TotalBsmtSF’ 似乎与 'SalePrice’呈线性正相关，这意味着一个变量增加，随之另一个变量也增加。并且’TotalBsmtSF’与 'SalePrice’的线性相关斜率较高。
• ‘OverallQual’ 和 'YearBuilt’似乎与 'SalePrice’有相关性，并且 ‘OverallQual’ 的相关性更强一些。箱线图显示了随着整体质量的增加，售价随之增高。

至此，我们只分析了四个变量，那么其他变量与 'SalePrice’又有什么关系呢？

三、多变量研究

至此我们都是主观地分析我们认为重要的因素，那么那些我们认为不那么重要的因素真的对销售价格没有影响吗？我们希望用数据分析出的结果客观地严谨地说明问题。
in[11]:

#查看列数
df_train.columns.size-2

out[11]:

79

可以看到，除销售价格以外，有79个因素可能影响销售价格（-2指去掉id列和saleprice列）。利用相关系数矩阵，可直观地了解这些因素与销售价格的相关度。
in[12]:

#相关系数矩阵
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);  
#热地图，vmax图例中最大值，square设定图片为正方形与否

out[12]:

注：heatmap()很好很强大！参数设置可参考：https://www.jianshu.com/p/e195a09a8ca9
从图上可以看到，‘TotalBsmtSF’ 和 '1stFlrSF’具有很强的相关性，并且 'Garage’类特征的相关性也非常高。（‘TotalBsmtSF’ 地下室面积， '1stFlrSF’一楼面积， ‘Garage’车库相关参数）事实上，这些相关性具有多重共线性。
另外，之前我们认为重要的因素 ‘GrLivArea’，‘TotalBsmtSF’，以及’OverallQual’ 都和销售价格有着很高的相关系数。
in[13]:

#销售价格相关系数矩阵
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index 
#nlargast()对corrmat切片，只保留‘SalePrice’列前10个最大值的所有行，cols为这些行的索引
cm = np.corrcoef(df_train[cols].values.T)  
#.T转置
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

out[13]:

注：‘OverallQual’：整体材料与表面质量
‘GrLivArea’：居住面积
‘GarageCars’：车库汽车可存放数量
‘GarageArea’：车库面积
‘TotalBsmtSF’：地下室总面积
‘1stFlrSF’：一楼面积
‘FullBath’：卧室数量
‘TotRmsAbvGrd’：地面以上客房总数（不含浴室）
‘YearBuilt’：建造年份

将与销售价格相关系数最高的前9个因素单独拿出来做相关系数矩阵热地图，我们分析得：
1、‘OverallQual’， ‘GrLivArea’ ， ‘TotalBsmtSF’ 确实与 ‘SalePrice’关系密切。
2、‘GarageCars’ 和 ‘GarageArea’ 也是重要因素，但是车库汽车数量与车库面积是同等的，因此，我们只考虑其一即可。这里我们可以保留相关系数更高的’GarageCars’。
3、 ‘TotalBsmtSF’ 与 '1stFlrSF’似乎也是等价关系？
4、 ‘FullBath’？
5、‘TotRmsAbvGrd’ 与 'GrLivArea’似乎也是等价关系？
6、‘YearBuilt’ 与 'SalePrice’的相关度在这9个因素中最弱。
（关于此，我们可以做时间序列分析来得到确切答案。）

再来看下’SalePrice’与相关因素的散点图吧。
in[14]:

#散点图
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(df_train[cols], size = 2.5)
plt.show();

注：pairplot()参数设置可参考：https://www.jianshu.com/p/6e18d21a4cad

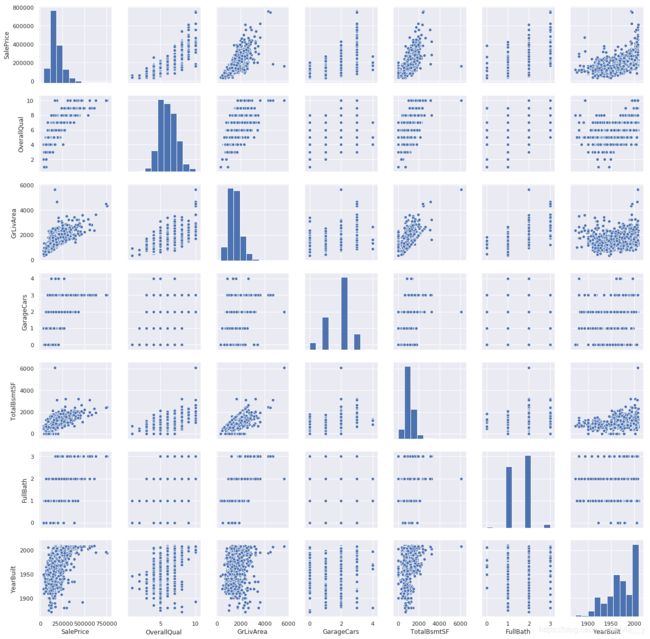
观察第五行第四列的图，是关于’GrLivArea’与 'TotalBsmtSF’的散点图。这些点几乎都在一条边界以下。地下室总面积可以等于居住面积，但预计地下室总面积不会比地上居住面积大。

四、清洗数据

1、缺失值

在处理缺失值时需要思考以下两个问题：

• 缺失值普遍性如何？
• 缺失是否有律可循？

由于实际原因，这两个问题很重要，因为数据缺失可能意味着样本量的减少，有可能影响分析结果。除此以外，我们需要保证对缺失值的处理不会出现偏离或隐藏事实。
in[15]:

#缺失值
total = df_train.isnull().sum().sort_values(ascending=False)
#isnull()返回布尔值，缺失值返回Ture。isnull().sum()返回缺失值的个数
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)
#head(n)前n行

注：sort_values()函数参数说明

DataFrame.sort_values(by, axis=0, ascending=True, inplace=False, kind='quicksort', na_position='last')  
#### 参数说明    
axis:{0 or ‘index’, 1 or ‘columns’}, default 0，默认按照索引排序，即纵向排序，如果为1，则是横向排序    
by:str or list of str；如果axis=0，那么by="列名"；如果axis=1，那么by="行名"；  
ascending:布尔型，True则升序，可以是[True,False]，即第一字段升序，第二个降序  
inplace:布尔型，是否用排序后的数据框替换现有的数据框  
kind:排序方法，{‘quicksort’, ‘mergesort’, ‘heapsort’}, default ‘quicksort’。似乎不用太关心  
na_position : {‘first’, ‘last’}, default ‘last’，默认缺失值排在最后面  
————————————————
版权声明：本文为CSDN博主「维格堂406小队 」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/wendaomudong_l2d4/article/details/80648633

out[15]:

若该变量15%的数据已经丢失，那么我们应当删除该变量并假设其不存在。

分析上述数据：
1、我们应当删除’PoolQC’，‘MiscFeature’，‘Alley’，‘Fence’，‘FireplaceQu’，'LotFrontage’这些变量，再者，这些因素也不是买房时我们主要会考虑到的。
2、再观察，'Garage’类的因素有着相同数量的丢失数据，很大可能丢失的是同一组观测数据。‘Bsmt’类的变量同理。
3、‘MasVnrType’（砖石饰面类型）与 ‘MasVnrArea’（砖石饰面面积）与’YearBuilt’ ‘OverallQual’ 有很强的关联性，我们可以考虑将这两个变量删除。
4、'Electrical’只有一个丢失数据，为此我们删除这条数据而保留变量。

总之，为处理缺失值，我们删除了所有缺失数据的变量（除了’Electrical’只删除缺失值这条数据）
in[16]

#缺失值处理
df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index,1)  #删除df_train的部分列
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index)  #删除行
df_train.isnull().sum().max() #检查是否遗漏缺失值

out[16]

0

2、异常值（离群点）

1、单变量分析
这里的关键在于如何建立阈值，如何定义一个观察值为异常值。为此我们将数据进行标准化，意味着把数据值转换成均值为0，方差为1的数据。
in[17]:

#数据标准化
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:,np.newaxis]);
#fit_transform 将数据拟合化后标准化（(X-mu)/）
low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
#排序，取前十个作为low_range，后十个作为high_range
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)

out[17]:

outer range (low) of the distribution:
[[-1.83820775]
 [-1.83303414]
 [-1.80044422]
 [-1.78282123]
 [-1.77400974]
 [-1.62295562]
 [-1.6166617 ]
 [-1.58519209]
 [-1.58519209]
 [-1.57269236]]

outer range (high) of the distribution:
[[3.82758058]
 [4.0395221 ]
 [4.49473628]
 [4.70872962]
 [4.728631  ]
 [5.06034585]
 [5.42191907]
 [5.58987866]
 [7.10041987]
 [7.22629831]]

对’SalePrice’进行标准化后：
1、低范围的值都比较相似并且在0附近分布。
2、高范围的值离0很远，并且7.几的值远在正常范围之外。

注：StandardScaler类是一个用来讲数据进行归一化和标准化的类。所谓归一化和标准化，即应用下列公式：
$X=(x-\mu )/\sigma$
使得新的X数据集方差为1，均值为0。

2、双变量分析
经过数据预处理之后，我们再来看下GrLivArea和SalePrice之间的关系。
in[18]:

var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

out[18]:

从图中我们看到，GrLivArea 有两个点非常大，显然并不太“合群”，我们可以大致猜测这两个点可能代表的是农业区的住房。但显然，这两个点可以作为异常值而删去。
SalePrice有两个在上文中提到需要注意的7.多的点，这两个点看似不合群，但整体符合大致房屋面积与住房的一个正比趋势，所以我们将这两个点保留。
in[19]:

#对GrLivArea排序，并找到对大的两个点
df_train.sort_values(by = 'GrLivArea', ascending = False)[:2]

out[19]:

in[20]:

#删除id为1299和523的数据
df_train = df_train.drop(df_train[df_train['Id'] == 1299].index)
df_train = df_train.drop(df_train[df_train['Id']== 523].index)

经过处理后，我们再来看下TotalBsmtSF和SalePrice之间的关系。

var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

我们可以删去TotalBsmtSF>3000的数据点，但问题不大，故这里我们先不做处理。

五、测试假设

我们已经做了一些数据清洗，分析了很多关于“SalePrice”的信息。我们再深入了解“SalePrice”如何符合统计假设，使我们能够应用多元技术。

检验四个假设：

• 正态性
  数据是否类似正态分布很重要，因为有几个统计模型依赖于正态分布（例如t-统计）。对于这个数据集，我们检查‘saleprice’的一元正态性（这是一个有限的方法），但是一元正态性并不能保证多元正态性的成立（这是我们想要的），但它对我们有帮助。另一个需考虑的细节是，在大样本（>200个观测值）中，正态性并不是这样的问题。然而，若我们解决了正态性，能够避免很多其他问题（例如异方差）。
• 同方差性
  同方差性是指“假设在预测变量的范围内，因变量的方差水平相同”。同方差是可取的，因为我们希望所有自变量的误差项都是相同的。
• 线性
  评估线性最常用的方法是检查散点图并搜索线性模式。如果模式不是线性的，那么研究数据转换是值得的。但是，我们不会深入讨论这个，因为我们看到的大多数散点图都是线性关系。
• 缺乏相关错误
  相关错误，如定义中所说的，发生于一个错误与另一个错误相关时。例如，如果一个正误差系统地产生了一个负误差，这意味着这些变量之间有关系。这通常发生在时间序列中，其中一些模式与时间相关。在此我们不做深入。但若您想检测到什么，试着添加一个变量并解释其产生的效果。这是相关错误最常见的解决方案。

正态性

检测“SalePrice”：

• 直方图-峰度和偏度。
• 正态概率图-数据分布应紧跟表示正态分布的对角线。

in[21]:

#直方图和正态概率图
sns.distplot(df_train['SalePrice'], fit=norm);#拟合标准正态分布

out[21]:
in[22]:

fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

out[22]:

注：P-P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图，用于直观地检测样本数据是否符合某一概率分布。如果被检验的数据符合所指定的分布，则代表样本数据的点应当基本在代表理论分布的对角线上。

可以看出，房价分布不是正态的，显示了峰值，正偏度，但是并不跟随对角线。在正偏态的情况下，我们可用对数变换对数据处理。

对数变换：数据分布的倾斜有很多负面的影响。我们可以使用特征工程技巧，利用统计或数学变换来减轻数据分布倾斜的影响。使原本密集的区间的值尽可能的分散，原本分散的区间的值尽量的聚合。Log变换通常用来创建单调的数据变换。它的主要作用在于帮助稳定方差，始终保持分布接近于正态分布并使得数据与分布的平均值无关。 关于特征工程详见：https://www.leiphone.com/news/201801/T9JlyTOAMxFZvWly.html

in[23]:

#对SalePrice应用Log变换
df_train['SalePrice'] = np.log(df_train['SalePrice'])

#log变换后的直方图和正态概率图
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

out[23]:

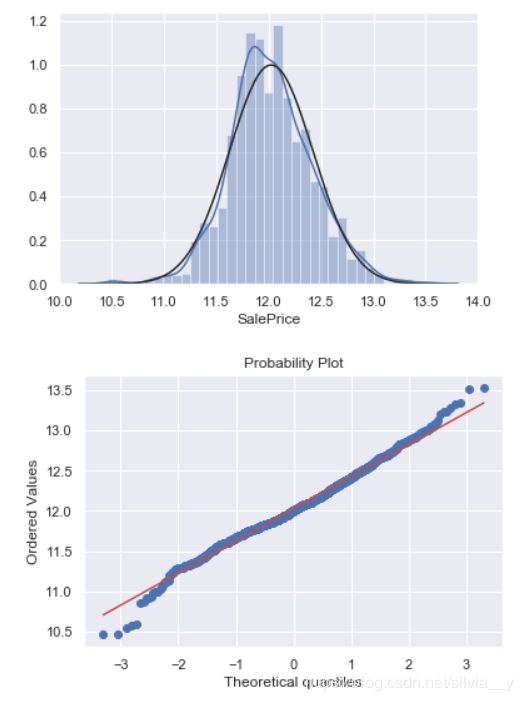
我们再来检测GrLivArea：
in[24]:

sns.distplot(df_train['GrLivArea'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)

out[24]：

同样，对GrLivArea也进行对数变换：
in[25]：

#对数变换
df_train['GrLivArea'] = np.log(df_train['GrLivArea'])

#变换后的直方图和正态概率图
sns.distplot(df_train['GrLivArea'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)

out[25]：

检测TotalBsmtSF：
in[26]:

sns.distplot(df_train['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['TotalBsmtSF'], plot=plt)

out[26]：

从图中我们可以看出：
1、显示除了偏度；
2、TotalBsmtSF有大量0观测值（表示有很多没有地下室的房子）。

而对数变换无法对0值进行变换。因此我们将非0值进行对数变换，对0值不做处理。这样既对数据进行了处理，也不会损失没有地下室的房屋信息。这种做法并不确定其正确性，但于我而言是可取的，但有风险。
in[27]:

#为新变量新建一列（由于新变量是二进制变量，故一列足矣），此新变量用于识别TotalBsmtSF中0与非0值
#若地下室面积>0，则取1，若地下室面积=0，则取0
df_train['HasBsmt'] = pd.Series(len(df_train['TotalBsmtSF']), index=df_train.index)
df_train['HasBsmt'] = 0 
df_train.loc[df_train['TotalBsmtSF']>0,'HasBsmt'] = 1

#对TotalBsmtSF进行log变换
df_train.loc[df_train['HasBsmt']==1,'TotalBsmtSF'] = np.log(df_train['TotalBsmtSF'])

sns.distplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], plot=plt)

out[27]：

同方差性

最好的测量两个变量的同方差性的方法就是图像。

#散点图
plt.scatter(df_train['GrLivArea'], df_train['SalePrice']);

在之前未对GrLivArea进行对数变换时的散点图呈现锥状，而经过对数变换后不再是锥形。通过保证某些变量的正态性，我们解决了同方差问题。

再来看看 ‘SalePrice’ 和 ‘TotalBsmtSF’：

#散点图
plt.scatter(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], df_train[df_train['TotalBsmtSF']>0]['SalePrice']);

总的来说，‘SalePrice’在整个‘TotalBsmtSF’范围内呈现相同的差异水平。

虚拟变量

将类别变量转换为虚拟变量：

df_train = pd.get_dummies(df_train)

总结

在这一kernel中，我们将 Hair et al. （2013）提出的很多策略付诸实践。我们对变量进行了一些主观性分析，不仅单独分析了SalePrice，也结合相关程度最高的变量进行分析。我们处理了缺失数据和异常值，也验证了一些基础统计假设，将类别变量转换为虚拟变量。
　　但问题还没有结束，我们还可以深入考虑预测房价的变化趋势，房价预测是否适合线性回归正则化的方法？是否适合组合方法？或者一些其他的方法？

文件说明：

    train.csv - the training set 训练集
    test.csv - the test set 测试集
    data_description.txt - 每列说明
    sample_submission.csv - 关于销售年月、大小、卧室数量的线性回归

列名说明：

    SalePrice - the property's sale price in dollars. This is the target variable that you're trying to predict.
    MSSubClass: The building class
    MSZoning: The general zoning classification
    LotFrontage: Linear feet of street connected to property
    LotArea: Lot size in square feet
    Street: Type of road access
    Alley: Type of alley access
    LotShape: General shape of property
    LandContour: Flatness of the property
    Utilities: Type of utilities available
    LotConfig: Lot configuration
    LandSlope: Slope of property
    Neighborhood: Physical locations within Ames city limits
    Condition1: Proximity to main road or railroad
    Condition2: Proximity to main road or railroad (if a second is present)
    BldgType: Type of dwelling
    HouseStyle: Style of dwelling
    OverallQual: Overall material and finish quality
    OverallCond: Overall condition rating
    YearBuilt: Original construction date
    YearRemodAdd: Remodel date
    RoofStyle: Type of roof
    RoofMatl: Roof material
    Exterior1st: Exterior covering on house
    Exterior2nd: Exterior covering on house (if more than one material)
    MasVnrType: Masonry veneer type
    MasVnrArea: Masonry veneer area in square feet
    ExterQual: Exterior material quality
    ExterCond: Present condition of the material on the exterior
    Foundation: Type of foundation
    BsmtQual: Height of the basement
    BsmtCond: General condition of the basement
    BsmtExposure: Walkout or garden level basement walls
    BsmtFinType1: Quality of basement finished area
    BsmtFinSF1: Type 1 finished square feet
    BsmtFinType2: Quality of second finished area (if present)
    BsmtFinSF2: Type 2 finished square feet
    BsmtUnfSF: Unfinished square feet of basement area
    TotalBsmtSF: Total square feet of basement area
    Heating: Type of heating
    HeatingQC: Heating quality and condition
    CentralAir: Central air conditioning
    Electrical: Electrical system
    1stFlrSF: First Floor square feet
    2ndFlrSF: Second floor square feet
    LowQualFinSF: Low quality finished square feet (all floors)
    GrLivArea: Above grade (ground) living area square feet
    BsmtFullBath: Basement full bathrooms
    BsmtHalfBath: Basement half bathrooms
    FullBath: Full bathrooms above grade
    HalfBath: Half baths above grade
    Bedroom: Number of bedrooms above basement level
    Kitchen: Number of kitchens
    KitchenQual: Kitchen quality
    TotRmsAbvGrd: Total rooms above grade (does not include bathrooms)
    Functional: Home functionality rating
    Fireplaces: Number of fireplaces
    FireplaceQu: Fireplace quality
    GarageType: Garage location
    GarageYrBlt: Year garage was built
    GarageFinish: Interior finish of the garage
    GarageCars: Size of garage in car capacity
    GarageArea: Size of garage in square feet
    GarageQual: Garage quality
    GarageCond: Garage condition
    PavedDrive: Paved driveway
    WoodDeckSF: Wood deck area in square feet
    OpenPorchSF: Open porch area in square feet
    EnclosedPorch: Enclosed porch area in square feet
    3SsnPorch: Three season porch area in square feet
    ScreenPorch: Screen porch area in square feet
    PoolArea: Pool area in square feet
    PoolQC: Pool quality
    Fence: Fence quality
    MiscFeature: Miscellaneous feature not covered in other categories
    MiscVal: $Value of miscellaneous feature
    MoSold: Month Sold
    YrSold: Year Sold
    SaleType: Type of sale
    SaleCondition: Condition of sale