NARX (Nonlinear autoregressive with external input) neural network学习

先看Wikipedia中的简要介绍：Nonlinear autoregressive exogenous model

In time series modeling, a nonlinear autoregressive exogenous model (NARX) is a nonlinear autoregressive model which has exogenous inputs. This means that the model relates the current value of a time series to both:

• past values of the same series; and
• current and past values of the driving (exogenous) series — that is, of the externally determined series that influences the series of interest.

In addition, the model contains:

• an "error" term

which relates to the fact that knowledge of other terms will not enable the current value of the time series to be predicted exactly.

Such a model can be stated algebraically as

Here y is the variable of interest, and u is the externally determined variable. In this scheme, information about u helps predict y, as do previous values of y itself. Here ε is the error term (sometimes called noise). For example, y may be air temperature at noon, and u may be the day of the year (day-number within year).

The function F is some nonlinear function, such as a polynomial. F can be a neural network, a wavelet network, a sigmoid network and so on. To test for non-linearity in a time series, the BDS test (Brock-Dechert-Scheinkman test) developed for econometrics can be used.

再来看一下Autoregressive model的介绍

In statistics, econometrics and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it is used to describe certain time-varying processes in nature, economics, etc. The autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term (an imperfectly predictable term); thus the model is in the form of a stochastic difference equation. In machine learning, an autoregressive model learns from a series of timed steps and takes measurements from previous actions as inputs for a regression model, in order to predict the value of the next time step.[1]

Together with the moving-average (MA) model, it is a special case and key component of the more general ARMA and ARIMA models of time series, which have a more complicated stochastic structure; it is also a special case of the vector autoregressive model (VAR), which consists of a system of more than one interlocking stochastic difference equation in more than one evolving random variable.

Contrary to the moving-average model, the autoregressive model is not always stationary as it may contain a unit root.

MATLAB中应用NARX的命令为narxnet，其解释如下：

NARX (Nonlinear autoregressive with external input) networks can learn to predict one time series given past values of the same time series, the feedback input, and another time series, called the external or exogenous time series

命令如下：

narxnet(inputDelays,feedbackDelays,hiddenSizes,trainFcn) takes these arguments,

inputDelays Row vector of increasing 0 or positive delays (default = 1:2)
feedbackDelays Row vector of increasing 0 or positive delays (default = 1:2)
hiddenSizes Row vector of one or more hidden layer sizes (default = 10)
trainFcn Training function (default = 'trainlm')

在narxnet中常常用到的两条命令：closeloop 和 preparets（用来重新准备数据，训练和测试前都可以使用此命令）

[Xs,Xi,Ai,Ts,EWs,shift] = preparets(net,Xnf,Tnf,Tf,EW)

Description

This function simplifies the normally complex and error prone task of reformatting input and target time series. It automatically shifts input and target time series as many steps as are needed to fill the initial input and layer delay states. If the network has open-loop feedback, then it copies feedback targets into the inputs as needed to define the open-loop inputs.

Each time a new network is designed, with different numbers of delays or feedback settings, preparets can reformat input and target data accordingly. Also, each time a network is transformed with openloop,closeloop, removedelay or adddelay, this function can reformat the data accordingly.

此函数简化了重新格式化输入和目标时间序列的通常复杂且容易出错的任务。 它会自动切换输入和目标时间序列，以填充初始输入和层延迟状态所需的步数。 如果网络具有开环反馈，则根据需要将反馈目标复制到输入中以定义开环输入。

每次设计新网络时，具有不同数量的延迟或反馈设置，准备就可以相应地重新格式化输入和目标数据。 此外，每次使用openloop，closeloop，removedelay或adddelay转换网络时，此函数都可以相应地重新格式化数据。

[Xs,Xi,Ai,Ts,EWs,shift] = preparets(net,Xnf,Tnf,Tf,EW) takes these arguments,

net	Neural network
Xnf	Non-feedback inputs
Tnf	Non-feedback targets
Tf	Feedback targets
EW	Error weights (default = {1})

 

and returns,

Xs	Shifted inputs
Xi	Initial input delay states
Ai	Initial layer delay states
Ts	Shifted targets
EWs	Shifted error weights
shift	The number of timesteps truncated from the front of X and T in order to properly fillXi and Ai.

closeloop

Convert neural network open-loop feedback to closed loop
Syntax
net = closeloop(net)
[net,xi,ai] = closeloop(net,xi,ai)

Description
net = closeloop(net) takes a neural network and closes any open-loop feedback. For each feedback output i whose property net.outputs{i}.feedbackMode is 'open', it replaces its associated feedback input and their input weights with layer weight connections coming from the output. The net.outputs{i}.feedbackMode property is set to 'closed', and the net.outputs{i}.feedbackInput property is set to an empty matrix. Finally, the value of net.outputs{i}.feedbackDelays is added to the delays of the feedback layer weights (i.e., to the delays values of the replaced input weights).

net = closeloop（net）采用神经网络并关闭任何开环反馈。 对于其属性net.outputs {i} .feedbackMode为“open”的每个反馈输出i，它将来自输出的层权重连接替换其关联的反馈输入及其输入权重。 net.outputs {i} .feedbackMode属性设置为'closed'，net.outputs {i} .feedbackInput属性设置为空矩阵。 最后，net.outputs {i} .feedbackDelays的值被添加到反馈层权重的延迟（即，替换的输入权重的延迟值）。

[net,xi,ai] = closeloop(net,xi,ai) converts an open-loop network and its current input delay states xi and layer delay states ai to closed-loop form.

closeloop的目的就是根据输入直接预测，而不需要输出的反馈，见下例：

[X,T] = simpleseries_dataset;
Xnew = X(81:100);
X = X(1:80);
T = T(1:80);
net = narxnet(1:2,1:2,10);
[Xs,Xi,Ai,Ts] = preparets(net,X,{},T);
net = train(net,Xs,Ts,Xi,Ai);
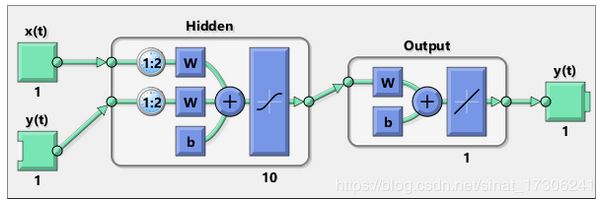
view(net)
[Y,Xf,Af] = net(Xs,Xi,Ai);

执行以下命令：

[Y,Xf,Af] = net(Xs,Xi,Ai);
perf = perform(net,Ts,Y)
[netc,Xic,Aic] = closeloop(net,Xf,Af);   %利用以前训练好的网络，把输出改成反馈
view(netc)

晚上再学习一下Simulink自带的几个神经网络控制器