自然语言处理：关系抽取之分段卷积神经网络（PCNN）

Tensorflow2.2实现，见github仓库。

远程监督

关系抽取训练集标注成本高，一般使用远程监督方法（半监督）自动标注数据。远程监督假设，若知识库中两个实体具有某种关系，则任何包含这两个实体的句子都具有这种关系。

下图为使用远程监督自动标注数据的实例，其中第一句标注正确，而第二句标注错误。

远程监督是快速获取关系抽取训练集的有效方法，但其有 两个缺点：

• 远程监督假设过于强烈，易标注错误，从而引入噪声数据，多数远程监督方法的研究聚焦于降噪；
• 远程监督多用于使用精细特征（句法结构等）的监督模型，这些特征一般使用已有的NLP工具提取，不可避免会引入误差，使用NLP工具提取的传统特征，会造成误差的传播或积累，而且，远程监督语料库多来源于网络的非正式文本，句子长度不一，随着句子长度的增加，传统特征提取的正确性会急剧下降；

PCNN关系抽取

Piecewise Convolutional Neural Networks (PCNNs) with multi-instance learning 解决以上两个难题：

为解决第一个问题，将远程监督关系抽取视为多实例问题。多实例问题中，训练集由很多包组成，每个包多个实例，每个包的标签已知，而包中实例的标签未知。设计目标函数只考虑每一个包的预测标签，PCNN仅选取每包中预测类别最接近真实类别的一个实例作为包的输出，一定程度上可降低包中一些实例标注错误的影响。

为解决第二个问题，使用CNN网络自动提取特征，不使用复杂的NLP预处理。对卷积层输出使用单一最大池化，能一定程度提取文本特征表达，但难以捕获两个实体间的结构信息。PCNN基于两实体位置信息将卷积层输出划分为3个部分，基于此，PCNN可能表现出更好的性能。

PCNN与Text CNN的主要区别在于输入层引入position embedding、池化层分为三段！

PCNN方法论

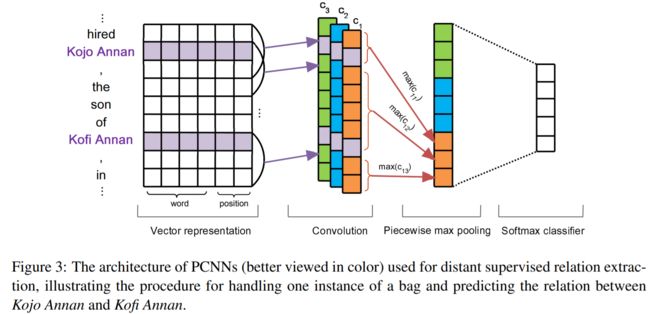
如图3所示，PCNNS主要由四部分组成：Vector Representation, Convolution, Piecewise Max Pooling and Softmax Output.

向量表达

句子的向量表达为两部分的拼接结果：词嵌入和位置嵌入。

• 使用skip-gram方法预训练词向量；
• 使用Position Embeddings表示句子单词到两个实体的相对距离，如下图，单词son到实体Kojo Annan和Kofi Annan的相对距离分别为3和-2。

随机初始化两个位置嵌入矩阵，图3中词嵌入的维度是4，位置嵌入的维度是1。结合词嵌入和位置嵌入，句向量表示为
$$S={\mathbb{R}}^{s\times d}$$

其中，$s$是句子长度（单词数），$d=d_w+d_p\ast 2$.

卷积层

对于长度为$s$的句子，首尾填充$w-1$长度，则卷积核$\mathbf{w}$的输出
$$\mathbf{c}\in {\mathbb{R}}^{s+w-1},c_j=\mathbf{w}{\mathbf{q}}_{j-w+1:j},1\le j\le s+w-1$$
若使用$n$个卷积核，则卷积操作的输出为
$$C=\{{\mathbf{c}}_1,\cdots ,{\mathbf{c}}_n\},c_{ij}={\mathbf{w}}_i{\mathbf{q}}_{j-w+1;j},1\le i\le n$$

图3中，卷积核的数目为3。

分段最大池化层

卷积层输出维度为${\mathbb{R}}^{n\times (s+w-1)}$，输出维度依赖于句子的长度。为便于应用于下游任务，卷积层的输出必须独立于序列长度，一般采用池化操作，主要思想是仅保留每个feature map中的主要的特征。

使用单一最大池化无法捕获两个实体的结构信息特征，PCNN使用分段最大池化代替单一最大池化，如图3所示，每个卷积核的输出${\mathbf{c}}_i$被两个实体划分为3部分，分段最大池化输出长度为3的向量：
$${\mathbf{p}}_i=\{p_{i1},p_{i2},p_{i3}\},p_{ij}=\max (c_{ij})1\le i\le n,1\le j\le 3$$
拼接所有卷积核分段池化层输出为${\mathbf{p}}_{1:n}$，经非线性函数输出为（维度与句子长度无关）
$$\mathbf{g}=\tanh ({\mathbf{p}}_{1:n}),\mathbf{g}\in {\mathbb{R}}^{3n}$$

Softmax层

首先将输出转化为类别分数（softmax转换为类别概率）
$$\mathbf{o}=W_1\mathbf{g}+b,W_1\in {\mathbb{R}}^{n_1\times 3n},\mathbf{o}\in {\mathbb{R}}^{n_1}$$

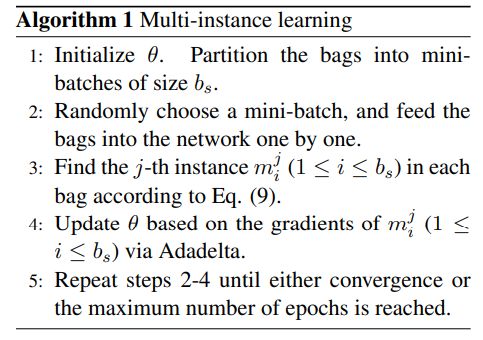
多实例学习

为降低数据标注错误的影响，PCNN使用多实例（半监督）学习。

考虑包含$T$个包的训练集$\{M_1,M_2,\cdots ,M_T\}$，其中$M_i=\{m_i^1,m_i^2,\cdots ,m_i^{q_i}\}$，包中$q_i$个不同实例互为独立。对于实例$m_i^j$，神经网络$\Theta$输出向量$\mathbf{o}$，其中第$r$个关系对应的概率为
$$p(r|m_i^j;\theta )=\frac{e^{o_r}}{{\sum }_{k=1}^{n_1}{e}^{o^k}}$$

将目标函数定义为极小化每个包的损失，从而降低包中部分数据标注错误的影响。每个包的标签已知，包中实例标签未知，训练过程中将包中实例在包标签上的最大概率作为预测输出，则目标函数定义为
$$J(\theta )=\sum _{i=1}^T\log p(y_i|m_i^j;\theta ),j^{\ast }=\arg \underset{j}{\max }p(y_i|m_i^j;\theta )$$

Reference

1. Distant Supervision for Relation Extraction via Piecewise Convolutional Neural Networks
2. EMNLP 2015 | PCNN实现远程监督在关系提取中的应用