基于MATLAB的混频测试
1、理论基础
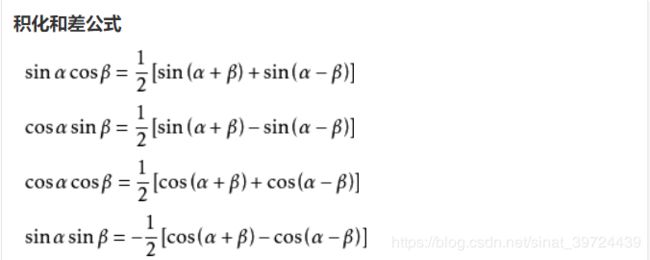
就是高中学习的公式。
从公式中可以看出,两个信号相乘后,可以得到两个信号频率和和差的叠加,
就比如在信号处理时,如果外部输入信号是5MHz,系统本振信号是10MHz,那经过这一系统后,可以得到5M和10M信号的叠加,如果经过一个低通滤波器,比如滤掉10M以上的信号。
2、matlab仿真
f1=5000000;
w1=2*pi*f1; %rad/s
f2=10000000;
w2=2*pi*f2; %rad/s
(1)s1=Asin(w1t+p); %正弦信号
(2)s2=Asin(w2t+p); %正弦信号
(3)s3 = s1.*s2;%混频信号
(4)s4=fft(s3,N);%傅里叶变换
(5)s5 = filter(b1,1,s3);%低通滤波
(6)s6=fft(s5,N);%傅里叶变换
(7)s7 = s3.*s2;%如果第三步被认为是调制的话,此过程可认为是解调
(8)s8=fft(s7,N);%傅里叶变换
(9)s9 = filter(b2,1,s7);%低通滤波
(10)s10=fft(s9,N);傅里叶变换
3、仿真图像
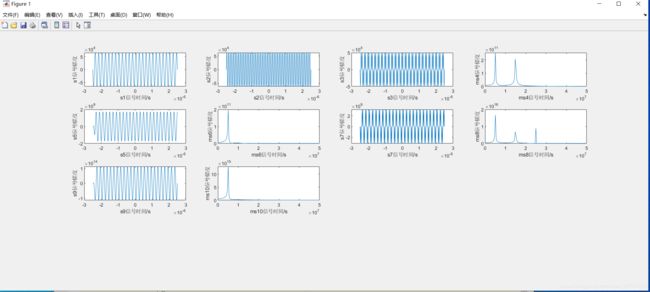
4、程序代码
%%
clear
close all
clc
%% signal
A=65535; %amplify
p=0; %rad
%采样
T=0.000005; %s %观测时间
f1=5000000; %Hz
w1=2pif1; %rad/s
f2=10000000;
w2=2pif2; %rad/s
fs=10f2; %Hz %采样频率
d=1/fs; %s %采样间隔
t=-T/2:d:T/2; %离散时间t
%%
s1=Asin(w1t+p); %正弦信号
s2=Asin(w2*t+p); %正弦信号
figure(1)
subplot(4,4,1),plot(t,s1);
xlabel(‘s1信号时间/s’);
ylabel(‘s1信号幅度’);
subplot(4,4,2),plot(t,s2);
xlabel(‘s2信号时间/s’);
ylabel(‘s2信号幅度’);
%%
s3 = s1.*s2;
subplot(4,4,3),plot(t,s3/65535);
xlabel(‘s3信号时间/s’);
ylabel(‘s3信号幅度’);
%%
N=256; %fft 点数
n=(0:(N-1))*fs/N;
s4=fft(s3,N);
ms4=abs(s4);
subplot(4,4,4),plot(n(1:N/2),ms4(1:N/2));
xlabel(‘ms4信号时间/s’);
ylabel(‘ms4信号幅度’);
%%
Fstop1 = (f1+f2)/2;
Wn1 = (2/fs)*Fstop1;
b1 = fir1(20,Wn1,‘low’,kaiser(21,3));
s5 = filter(b1,1,s3);
subplot(4,4,5),plot(t,s5);
xlabel(‘s5信号时间/s’);
ylabel(‘s5信号幅度’);
%%
N=256; %fft 点数
n=(0:(N-1))*fs/N;
s6=fft(s5,N);
ms6=abs(s6);
subplot(4,4,6),plot(n(1:N/2),ms6(1:N/2));
xlabel(‘ms6信号时间/s’);
ylabel(‘ms6信号幅度’);
%%
s7 = s3.*s2;
subplot(4,4,7),plot(t,s7/65535);
xlabel(‘s7信号时间/s’);
ylabel(‘s7信号幅度’);
%%
N=256; %fft 点数
n=(0:(N-1))*fs/N;
s8=fft(s7,N);
ms8=abs(s8);
subplot(4,4,8),plot(n(1:N/2),ms8(1:N/2));
xlabel(‘ms8信号时间/s’);
ylabel(‘ms8信号幅度’);
%%
Fstop2 = (f1+f2)/2;
Wn2 = (2/fs)*Fstop2;
b2 = fir1(20,Wn2,‘low’,kaiser(21,3));
s9 = filter(b2,1,s7);
subplot(4,4,9),plot(t,s9);
xlabel(‘s9信号时间/s’);
ylabel(‘s9信号幅度’);
%%
N=256; %fft 点数
n=(0:(N-1))*fs/N;
s10=fft(s9,N);
ms10=abs(s10);
subplot(4,4,10),plot(n(1:N/2),ms10(1:N/2));
xlabel(‘ms10信号时间/s’);
ylabel(‘ms10信号幅度’);